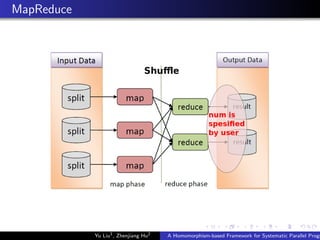
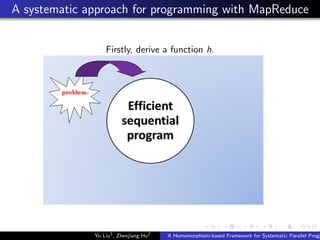
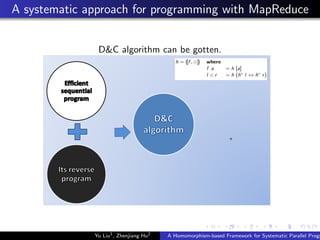
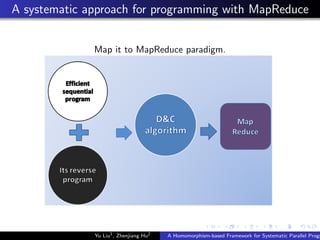
This document describes a homomorphism-based framework for systematic parallel programming with MapReduce. The framework introduces a systematic approach to automatically generate fully parallelized and scalable MapReduce programs. It provides algorithmic programming interfaces that allow users to focus on the algebraic properties of problems, hiding the details of MapReduce. The framework was implemented on top of Hadoop and evaluated on several test problems, demonstrating good scalability and parallelism. Future work could decrease system overhead, optimize performance further, and extend the framework to more complex data structures like trees and graphs.

1. A Homomorphism-based Framework for
Systematic Parallel Programming with MapReduce
Yu Liu1, Zhenjiang Hu2
1 The Graduate University for Advanced Studies,Tokyo, Japan
yuliu@nii.ac.jp
2 National Institute of Informatics,Tokyo, Japan
2 hu@nii.ac.jp
Mar. 10th, 2011
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

2. Background
MapReduce
Google’s MapReduce is a popular parallel-distributed programming
model, for processing large data sets. It has been the de facto
standard for large scale data analysis.
Concepts from functional programming languages
Automatic parallel processing, fault tolerance
Good scalability
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

3. MapReduce
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

4. MapReduce
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

5. MapReduce
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

6. MapReduce
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

7. MapReduce
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

8. Programming with MapReduce
A user has to
design a D&C algorithm that fits MapReduce paradigm
map this algorithm to MapReduce.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

9. Programming with MapReduce
A user has to
design a D&C algorithm that fits MapReduce paradigm
map this algorithm to MapReduce.
Difficulties of programming with MapReduce
How to resolve the constrains on computing order.
How to resolve the data dependency.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

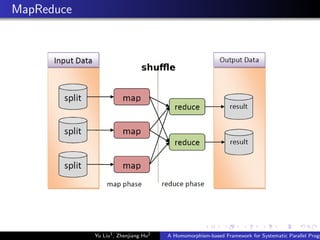
10. Example
The Maximum Prefix Sum problem
mps [3, −1, 4, −1, −5, 9, 2, −6, 5, −10] = 11
A sequential program for MPS in O(n) time
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

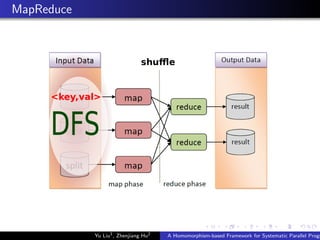
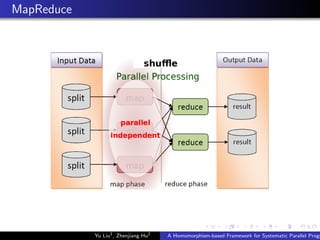
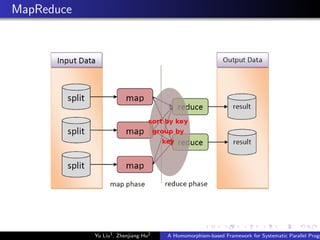
11. Example
The Maximum Prefix Sum problem
mps [3, −1, 4, −1, −5, 9, 2, −6, 5, −10] = 11
Hard to compute MPS with MapReduce
Computation has order.
MPS of sub-lists cannot be conquered directly.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

12. Questions
Is there a systematic way to resolving such problems with
MapReduce ?
How to handle the problems with district order ?
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

13. Questions
Is there a systematic way to resolving such problems with
MapReduce ?
How to handle the problems with district order ?
How to systematically design the divide-and-conquer
algorithm ?
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

14. Motivation and objective
We propose a systematic approach to automatically generate fully
parallelized and scalable MapReduce programs.
A new framework which provides algorithmic programming
interfaces has been implemented.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

15. A systematic approach for programming with MapReduce
Firstly, derive a function h.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

16. A systematic approach for programming with MapReduce
Then write a inverse function h◦.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

17. A systematic approach for programming with MapReduce
D&C algorithm can be gotten.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

18. A systematic approach for programming with MapReduce
Map it to MapReduce paradigm.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

19. A systematic approach for programming with MapReduce
Parallelization is in a black box.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

20. A systematic approach for programming with MapReduce
Implemented by multi-phases MapReduce processing.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

21. Conditions of this f function
Theorem
If there exists a binary operator such that
f (xs ++ ys) = f xs f ys
then such can be defined as :
x y = f (f ◦x ++ f ◦x)
where ++ islistconcatenation.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

22. Iff a function can be defined both rightwards and leftwards, such
exists. We can derive a divide-and-conquer algorithm like this:
Divide-and-conquer
f (xs ++ ys) = f (f ◦
(f xs) ++ f ◦
(f ys))
Such functions are so called: homomorphisms.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

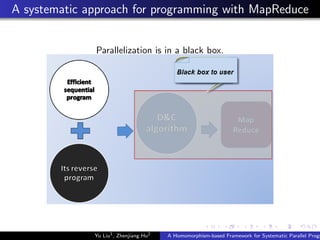
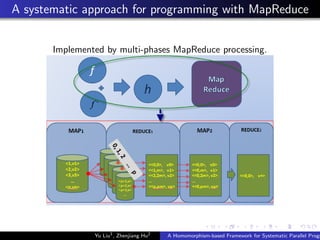
23. Programming Interface
Fold and unfold
fold :: [α] → β
unfold :: β → [α].
The implementation in Java
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

24. A function which computes MPS and its right inverse can be
written as followings:
fold xs = mps sum xs
unfold (m, s) = [m, s − m]
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

25. The computation inside framework
Use fold and unfold functions doing the computation:
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

26. Autonomous intermediate data
Each record of the intermediate data has the information of
position, thus the distribution of data is indifferent.
< id, val > → << parId, id >, val >
By taking use of sorting and grouping mechanism of MapReduce
framework, lists can be reconstructed when necessary.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

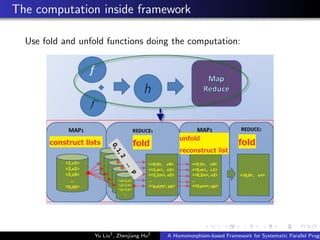
27. A formal definitation
homMR
homMR :: (α → β) → (β → β → β) → {(ID, α)} → β
homMR f (⊕) = getValue ◦ MapReduce mapper2 reducer2
◦ MapReduce mapper1 reducer1
where
mapper1 :: (ID, α) → [((PID, ID), α)]
mapper1 (i, a) = [(pid, i), a))]
where pid = makePid i
reducer1 :: ((PID, ID), [α]) → ((PID, ID), β)
reducer1 ((pid, j), ias) = ((pid, j), hom f (⊕) ias)
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

28. continued
mapper2 :: ((PID, ID), β) → ((PID, ID), β)
mapper2 ((pid, j), b) = ((c0, j), b)
where c0 is a predefined constant pid
reducer2 :: ((PID, ID), [β]) → ((PID, ID), β)
reducer2 ((c0, k), jbs) = ((c0, k), hom f (⊕) jbs)
getValue :: ((PID, ID), β) → β
getValue ((c0, k), c) = c
Where, hom f (⊕) denotes a sequential version of ([f , ⊕]).
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

29. Actual user-program for MPS
http://screwdriver.googlecode.com
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

30. Performance evaluation
Environment: hardware
We configured clusters with 2, 4, 8, and 16 nodes. Each
computing/data node has two Xeon CPUs (Nocona, single-core,
2.8 GHz), 2 GB memory. The nodes are connected with Gigabit
Ethernet.
Environment: software
Linux2.6.26 ,Hadoop 0.21.0 +HDFS
Hadoop configuration: heap size= 1024MB
maximum mapper per node: 2
maximum reducer per node: 1
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

31. Test cases
We implemented several programs for three problems on our
framework and Hadoop:
1 the maximum-prefix-sum problem.
MPS-lh is implemented using our framework’ API.
MPS-mr is implemented by Hadoop API.
2 parallel sum of 64-bit integers
SUM-lh is implemented by our framework’ API.
SUM-mr is implemented by Hadoop API.
3 VAR-lh computes the variance of 32-bit floating-point
numbers;
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

32. Test cases
Test data
100 million 64-bit integers (2.87 GB) for MPS, SUM.
100 million 32-bit floating-point numbers (2.76 GB) for VAR.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

33. Performance
The experiment results are summarized :
With 16 nodes speedup of all cases are more than 7.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

34. Performance
Time curves:
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

35. Concluding remarks
In this research:
Introduced a systematic way of parallel programming on
MapReduce.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

36. Concluding remarks
In this research:
Introduced a systematic way of parallel programming on
MapReduce.
Developed a framework on top of Hadoop.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

37. Concluding remarks
In this research:
Introduced a systematic way of parallel programming on
MapReduce.
Developed a framework on top of Hadoop.
Algorithmic programming interfaces let user can focus on the
algebraic properties of problem.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

38. Concluding remarks
In this research:
Introduced a systematic way of parallel programming on
MapReduce.
Developed a framework on top of Hadoop.
Algorithmic programming interfaces let user can focus on the
algebraic properties of problem.
Details of MapReduce are hidden.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

39. Concluding remarks
In this research:
Introduced a systematic way of parallel programming on
MapReduce.
Developed a framework on top of Hadoop.
Algorithmic programming interfaces let user can focus on the
algebraic properties of problem.
Details of MapReduce are hidden.
Achieved good scalability and parallelism.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

40. Concluding remarks
In this research:
Introduced a systematic way of parallel programming on
MapReduce.
Developed a framework on top of Hadoop.
Algorithmic programming interfaces let user can focus on the
algebraic properties of problem.
Details of MapReduce are hidden.
Achieved good scalability and parallelism.
Automatic optimization can be equipped.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

41. Future work
Decrease the system overhead and do more optimization.
Extend to more complex data structure such as tree and
graph.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

42. Related work
Parallel programming with list homomorphisms (M.Cole 95)
The Third Homomorphism Theorem(J.Gibbons 96).
Systematic extraction and implementation of
divide-and-conquer parallelism (Gorlatch PLILP96).
Automatic inversion generates divide-and-conquer parallel
programs(Morita et.al., PLDI07).
The third homomorphism theorem on trees: downward &
upward lead to divide-and-conquer (Morihata, POPL09)
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

43. Thank you very much.
Questions?
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

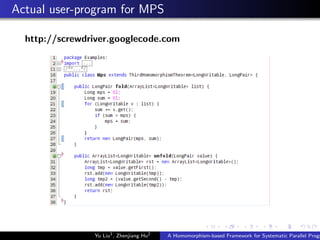
44. List Homomorphism
Function h is said to be a list homomorphism
If there are a function f and an associative operator such that
for any list x and list y
h [a] = f a
h (x ++ y) = h(x) h(y).
Where ++ is the list concatenation.
Instance of a list homomorphism
sum [a] = a
sum (x ++ y) = sum x + sum y.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

45. Theorem (The Third Homomorphism Theorem (Gibbons,96) )
Let h be a given function and and be binary operators. If the
following two equations hold for any element a and list y
h ([a] ++ y) = a h y
h (y ++ [a]) = h y a
then the function h is a homomorphism.
In fact, for a function h, if we have one of its right inverse h◦ that
satisfies h ◦ h◦ ◦ h = h, then we can obtain the list-homomorphic
definition as follows.
h = ([f , ]) where
f a = h [a]
l r = h (h◦ l ++ h◦ r)
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

46. MapReduce programs can be automatically obtained by
two sequential functions
homomorphism ([f , ⊕])
f :: a → b
⊕ :: b → b → b
(a ⊕ b) ⊕ c = a ⊕ (b ⊕ c).
fold and unfold, that compose leftwards and rightwards functions
fold([a] ++ x) = fold([a] ++ unfold(fold(x)))
fold(x ++ [a]) = fold(unfold(fold(x)) ++ [a]).
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

47. Currently, Screwdriver provides two kinds of programming
interfaces:
Programming interface corresponding to definition of list
homomorphism;
Programming interface corresponding to the 3rd
homomorphism theorem.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

48. Basic Homomorphism-Programming Interface
Two functions which define an homomorphism
filter :: a → b
plus :: b → b → b.
The implementation in Java
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

49. Programming Interface based on the 3rd homomorphism
theorem
A function and its right inverse
fold :: [a] → b
unfold :: b → [a].
The implementation in Java
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

50. The implementation of Screwdriver : list representation
To implement our programming interface with Hadoop, we need to
consider how to represent lists in a distributed manner.
Input data: index-value pairs
We use integer as the index’s type, the list [a, b, c, d, e] is
represented by {(3, d), (1, b), (2, c), (0, a), (4, e)}.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

51. Partition of input list
The pid(partition-id) of type PID is the index of a partial list. The
framework produces a same pid for the records which will be
grouped together. These records have continues id.
Intermediate data: nested pairs ((pid, id), val)
Suppose the above list was divided to two parts and in different
nodes, then they are represented as
{((0, 1), b), ((0, 2), c), ((0, 0), a)} and {((1, 3), d), ((1, 4), e)}.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

52. Grouping and sorting of intermediate data
We defined two functions: the comparatorG and comparatorS as
follows:
comparatorG (pid1, id1) (pid2, id2) = if pid1 == pid2
then 0
else − 1
comparatorS (pid1, id1) (pid2, id2) = if id1 > id2
then 1
else − 1
for grouping intermediate records with same pid and sorting them
by id.
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr

53. Data partition
1 In MAP task,
intermediate records with same pid are grouped together and
sorted by id.
a partitioner dispatches the groups to different reducers.
2 In REDUCE task, reducers apply merge-sort on all groups
with same pid
Yu Liu1
, Zhenjiang Hu2
A Homomorphism-based Framework for Systematic Parallel Progr