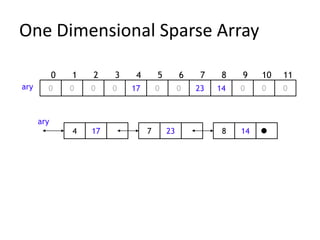
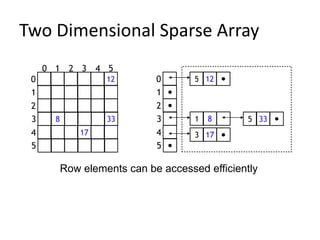
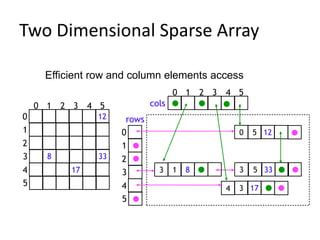
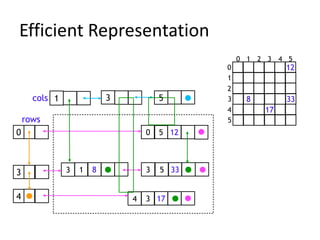
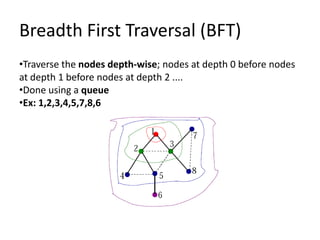
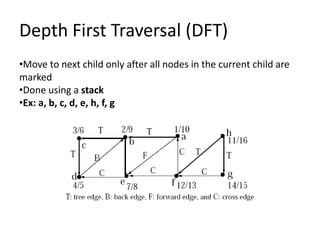
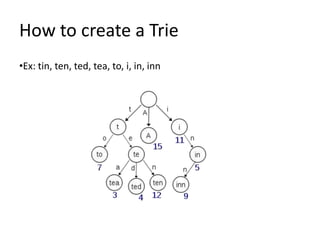
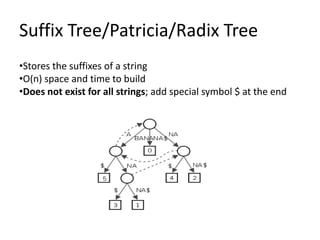
Data structures allow for efficient representation of data and solutions to real-world problems like insertion, deletion, search, and sort. Common data structures include arrays, linked lists, stacks, queues, trees, and hashes. Arrays use contiguous memory allocation while linked lists connect elements using pointers. Trees and hashes are useful for modeling hierarchical and associative data respectively. Recursion and traversal algorithms like breadth-first and depth-first are used to process tree and graph structures.

2. Why we need Data Structures?
•Efficient and Intuitive representation of data
•Tree using arrays vs tree using pointers
•To solve real life problems efficiently
•Insertion
•Deletion
•Search
•Sort
•Applications
•Social networks
•Employee hierarchy
•Recommended items

3. Basic Operations
1.traverse
2.insert
3.delete
4.find

4. Data Structures (Basic)
•Arrays
•Linked Lists
•Stacks
•Queues
•Recursion
•Trees – Basic
•Practice Problems

5. Arrays

6. •Contiguous and fixed memory allocation (independent of
language)
•Random access and modification
•List of (index, value); index is non-negative integer; all values in
a given array are of the same data type
•To hold various types of values or have non-numerical indices,
use associative arrays/dictionaries – The Dictionary Problem?

7. •Arrays may also be:
•2-D : array of 1-D arrays (a 1-D array is a data type in itself)
•3-D : array of 2-D arrays (a 2-D array is a data type in itself)
•Memory placement of multi-dimensional arrays
1.row-major
2.column-major
•Useful Operation
a.Modify
b.Access
c.Swap
d.In-place reverse

8. Structure of an Array
template<class T> class Array{
int size;
T *arr;
void put();
void get();
…….
};
Useful Libraries
#include <vector>

9. Irregular Arrays
•Languages known to students at IITG
1.2-D Array
Languages
Student
1.Irregular Array
Student

10. Special (Arrays ??)
•Diagonal matrix, upper/lower triangular matrix, trigonal matrix,
symmetric/asymmetric matrices
•Generally deal with 2-D matrices, but 3-D or higher cases are
also possible. Generally deal with square matrix, but rectangular
(non-square) are also possible
•More like functions

11. Special (Arrays ??)
int spec_matrix(int i, int j){
return no_cols*i + j + 1;
}
•Performance ??

12. One Dimensional Sparse Array
0 1 2 3 4 5 6 7 8 9 10 11
ary 0 0 0 0 17 0 0 23 14 0 0 0
ary
4 17 7 23 8 14

13. Two Dimensional Sparse Array
0 1 2 3 4 5
0 12 0 5 12
1 1
2 2
3 8 33 3 1 8 5 33
4 17 4 3 17
5 5
Row elements can be accessed efficiently

14. Two Dimensional Sparse Array
Efficient row and column elements access
0 1 2 3 4 5
0 1 2 3 4 5 cols
0 12 rows
1 0 0 5 12
2 1
3 8 33 2
4 17 3 3 1 8 3 5 33
5 4 4 3 17
5

15. Efficient Representation
0 1 2 3 4 5
0 12
1
2
cols 1 3 5 3 8 33
4 17
rows 5
0 0 5 12
3 3 1 8 3 5 33
4 4 3 17

16. Linked Lists

17. Why?
•To store heterogeneous data
•To store sparse data
•Flexibility of increase/decrease in size; easy insertion and
deletion of elements
•Useful Operations
•insertion
•deletion

19. The Structure
template <class T> class node{
T data;
node<T> *next; // Extra (4?) bytes; size of a pointer
};
template <class T> LinkedList{
node<T> *head;
int size; // …..etc etc etc
};
Useful Libraries
#include <list>

21. Insertion/Deletion
Time Complexity:
Insertion : O(1) / O(n)
Deletion : O(1) / O(n)
Space Complexity:
Insertion : O(1)
Deletion : O(1)

22. Tweak some more !
•Doubly Linked Lists
•Extra (4?) bytes space vs better accessibility
•Insertion/deletion ?
•Circular Linked Lists
•How to find the end?
•Tail pointer
•Null ‘next’ pointer from last node
•Last node points to first (circular)

23. Practice (Linked List)
Linked List 1)
Linked List 2)

24. Recursion

25. •To solve a task using that task itself
•; a task should have recursive nature
•; generally can be transformed by tweaking some parts of the
task
•Example: task of piling up n coins vs picking up a
suitcase.
•Let the task be a C function. What are the parts of the
task:
1.Input it takes
2.What it does
3.Output it gives

26. •A task is performed recursively when generally a large input
can’t be handled directly.
•So, recursion is all about simplifying the input at every step till it
becomes trivial (base case)

27. Implementation – run time stack
•Activation Records (AR)
•Store the state of a method
1.input parameters
2.return values
3.local variables
4.return addresses

30. Advantages/Disadvantages
1.more readable/understandable/consistent with the the
definition
1.memory requirements increase due to runtime stack
2.difficult to open and debug

31. Types of Recursion
•Tail (vs loop?)
int factn;
While (n > 0) factn *= n--;
•Indirect
•A() -> B() -> C() -> A()
•Nested:
•h(n) = h(2 + h(n-1))

33. Hashes

34. Why?
•Want to store dictionaries?, associative arrays?
•arrays with non-numerical indices
•String operations made easy
•Ex: Finding anagrams
•Ex: Counting frequency of words in a string

35. Associative Arrays
•(key, value) pairs where key is not necessarily a non-negative
integer; can be string etc.
•Ex: no. of students in each department
•“cse” => 68
•“eee” => 120
•“mech” => 70
•“biotech” => 30
•Do not allow duplicate keys
•Dict (“cse”) = “data structures”
•Dict (“cse”) = “algorithms”
Dict(“cse”) = {“data structures”, “algorithms”}

36. Hash Functions
1.HashTable : an array of fixed size
•TableSize - preferably prime and large
2.Hash function (map to an index of the HashTable)
Techniques
•use all characters
•use aggregate properties - length, frequencies of
characters
•first 3 characters, odd characters
Evaluation
•Uniform distribution; load factor λ?
•Utilize table space
•Quickly computable

37. 3. Collision resolution
1.separate chaining
•Linked list at each index
•Insertion (at head?)
•Desired length of a chain : close to λ
•Avg. time for Successful search = 1 + 1 + λ/2
•Disadvantages
•slow?
•different data structures - array/linked lists?

38. 1.open addressing
•Single table
•Desired λ ~ 0.5
•Apply h0(x), h1(x), h2(x) …
• hi(x) = h(x) + f(i); f(0) = 0
3 ways to do it
1.linear probing : f(i) is linear in i
•f(i) = i (quickly computable vs primary clustering?)
2.quadratic probing : f(i) is quadratic in i
3.double hashing
•H(x) = h(x) + f(i).h2(x)
Rehashing
•What if the table gets full (70%, …. , 100%)
•Create a new HashTable double? the size

39. Structure
template<class T> class Hash{
int TableSize;
T *arr;
};
Useful Libraries
#include <hash>

40. Practice (Hashes)
Trie 7)

41. Graphs

43. Representation
1.Adjacency Matrix (|V| * |V|)
1.Adjacency List

44. Breadth First Traversal (BFT)
•Traverse the nodes depth-wise; nodes at depth 0 before nodes
at depth 1 before nodes at depth 2 ....
•Done using a queue
•Ex: 1,2,3,4,5,7,8,6

45. Depth First Traversal (DFT)
•Move to next child only after all nodes in the current child are
marked
•Done using a stack
•Ex: a, b, c, d, e, h, f, g

46. Trees (Advanced)

47. Retrieval
•Stores the prefixes of a set of strings in an efficient manner
•Used to store associative arrays/dictionaries

48. How to create a Trie
•Ex: tin, ten, ted, tea, to, i, in, inn

49. Pairs of anagrams
•Sort all the strings
•acute -> acetu
•obtuse -> beostu … etc
•Insert them into the trie
•Keep storing collisions i.e. multiple values for each key
•Each set of values gives groups of anagrams

50. Suffix Tree/Patricia/Radix Tree
•Stores the suffixes of a string
•O(n) space and time to build
•Does not exist for all strings; add special symbol $ at the end

51. Advantages of Suffix Trees
•Store n suffixes in O(n) space.
•Improved string operations. Eg. substring lookup, Longest
common substring operation (generalized suffix trees?)
Generalized Suffix Trees
•Each string terminated by a different special symbol
•More space efficient
•Have different set of algorithms

52. Longest Common Substring
Longest Common Substring
1.Make a “generalized suffix tree” for the (2?) strings
2.Traverse the tree to mark all internal nodes as 1, 2 or (1,2)
depending on whether it is parent to a leaf node terminating
with the special symbol of string 1 and string 2.
3.Find the deepest internal node marked 1,2
Pattern Matching ?