The document outlines a homomorphism-based framework for parallel programming on MapReduce. It introduces homomorphisms and theorems about them. The framework represents lists as sets of key-value pairs distributed across nodes. Functions are implemented using this representation and MapReduce, allowing easy parallelization of problems like maximum prefix sum that are otherwise complex on MapReduce.

1. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
A Homomorphism-based MapReduce Framework
for Systematic Parallel Programming
Yu Liu
The Graduate University for Advanced Studies
Jan 12, 2011
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

2. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Outline
1 Motivations
2 Brief introduction of MapReduce
3 The Homomorphism-based Framework
4 Case Study: Parallel sum, Maximum prefix sum, Variance of
numbers
5 Experimental Results
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

3. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Motivation of This Talk
Show how to make programming with MapReduce easier.
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

4. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Motivation of This Talk
Show how to make programming with MapReduce easier.
Introduce an approach of automatic parallel program
generating.
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

5. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Programming Paradigm of MapReduce
List Homomorphism and Homomorphism Theorems
MapReduce Programming model
The Computation of MapReduce Framework
Google’s MapReduce is a parallel-distributed programming model,
together with an associated implementation, for processing very
large data sets in a massively parallel manner.
Components of a MapReduce program (Hadoop)
A Mapper;
A Partitioner that can be used shuffling data;
A Combiner that can be used doing local reduction;
A Reducer ;
A Comparator can be used while sorting or grouping;
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

6. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Programming Paradigm of MapReduce
List Homomorphism and Homomorphism Theorems
MapReduce Programming model
MapReduce Data-processing flow
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

7. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Programming Paradigm of MapReduce
List Homomorphism and Homomorphism Theorems
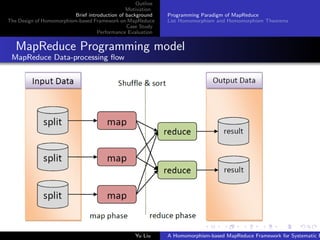
MapReduce Programming model
A simple functional specifcation of the MapReduce framework
Function mapS is a set version of the map function. Function
groupByKey :: {[(k, v)]} → {(k, [v])} takes a set of list of
key-value pairs (each pair is called a record) and groups the values
of the same key into a list.
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

8. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Programming Paradigm of MapReduce
List Homomorphism and Homomorphism Theorems
Maximum Prefix Sum problem
The Maximum Prefix Sum problem (mps) is to find the maximum
prefix-summation in a list:
3, −1, 4, 1, −5, 9, 2, −6, 5
This problem seems not obvious to solve this problem efficiently
with MapReduce.
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

9. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Programming Paradigm of MapReduce
List Homomorphism and Homomorphism Theorems
List Homomorphism
Function h is said to be a list homomorphism
If there are a function f and an associated operator such that
for any list x and list y
h [a] = f a
h (x ++ y) = h(x) h(y).
Where ++ is the list concatenation.
For instance, the function sum can be described as a list
homomorphism
sum [a] = a
sum (x ++ y) = sum x + sum y.
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

10. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Programming Paradigm of MapReduce
List Homomorphism and Homomorphism Theorems
List Homomorphism and Homomorphism Theorems
Leftwards function
Function h is leftwards if it is defined in the following form with
function f and operator ⊕,
h [a] = f a
h ([a] ++ x) = a ⊕ h x.
Rightwards function
Function h is rightwards if it is defined in the following form with
function f and operator ⊗,
h [a] = f a
h (x ++ [a]) = h x ⊗ a.
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

11. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Programming Paradigm of MapReduce
List Homomorphism and Homomorphism Theorems
List Homomorphism and Homomorphism Theorems
Map and Reduce
For a given function f , the function of the form ([[·] ◦ f , ++ ]) is a
map function, and is written as map f .
————————————————————————————
The function of the form ([id, ]) for some is a reduce function,
and is written as reduce ( ).
The First Homomorphism Theorem
Any homomorphism can be written as the composition of a map
and a reduce:
([f , ]) = reduce ( ) ◦ map f .
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

12. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Programming Paradigm of MapReduce
List Homomorphism and Homomorphism Theorems
List Homomorphism and Homomorphism Theorems
The Third Homomorphism Theorem
Function h can be described as a list homomorphism, iff ∃ and
∃ f such that:
h = ([f , ])
if and only if there exist f , ⊕, and ⊕ such that
h [a] = f a
h ([a] ++ x) = a ⊕ h x
h (x ++ [b]) = h x ⊗ b.
The third homomorphism gives a necessary and sufficient condition
for the existence of a list homomorphism.
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

13. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
A homomorphism-based framework wrapping MapReduce
To make it easy for resolving problems such as mps by
MapReduce. We using the knowledge of homomorphism especially
the third homomorphism theorem to wrapping MapReduce model.
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

14. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
A homomorphism-based framework wrapping MapReduce
Basic Homomorphism-Programming Interface
filter :: a → b
aggregator :: b → b → b.
The implementlation on Hadoop
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

15. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
A homomorphism-based framework wrapping MapReduce
A simple example of using this interface for computing the sum of
a list
The implementlation on Hadoop
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

16. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
A homomorphism-based framework wrapping MapReduce
Programming Interface with Right Inverse
fold :: [a] → b
unfold :: b → [a].
The implementlation on Hadoop
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

17. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
A homomorphism-based framework wrapping MapReduce
A simple example of using this interface for computing the sum of
a list
The implementlation on Hadoop
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

18. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
A homomorphism-based framework wrapping MapReduce
Requirements of using this interface in addition to the right-inverse
property of unfold over fold.
Both leftwards and rightwards functions exist
fold([a] ++ x) = fold([a] ++ unfold(fold(x)))
fold(x ++ [a]) = fold(unfold(fold(x)) ++ [a]).
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

19. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
The implementation of homomorphism framework upon
Hadoop
To implement our programming interface with Hadoop, we need to
consider how to represent lists in a distributed manner.
Set of pairs as list
We use integer as the index’s type, the list [a, b, c, d, e] is
represented by {(3, d), (1, b), (2, c), (0, a), (4, e)}.
Set of pairs as distributed List
We can represent the above list as two sub-sets
{((0, 1), b), ((0, 2), c), ((0, 0), a)} and {((1, 3), d), ((1, 4), e)}, each
in different data-nodes
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

20. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
The implementation of homomorphism framework upon
Hadoop
The first homomorphism theorem implies that a list
homomorphism can be implemented by MapReduce, at least two
passes of MapReduce.
Defination of homMR
homMR :: (α → β) → (β → β → β) → {(ID, α)} → β
homMR f (⊕) = getValue ◦ MapReduce mapper2 reducer2
◦ MapReduce mapper1 reducer1
where
mapper1 :: (ID, α)) → [((ID, ID), β))]
mapper1 (i, a) = [((pid, i), b)]
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

21. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
The implementation of homomorphism framework upon
Hadoop
Defination of homMR
reducer1 :: (ID, ID) → [β] → β
reducer1 ((p, j), ias)) = hom f (⊕) ias
mapper2 :: ((ID, ID), β) → [((ID, ID), β)]
mapper2 ((p, j), b) = [((0, j), b)]
reducer2 :: (ID, ID) → [β] → β
reducer2 ((0, k), jbs) = hom (⊕) jbs
getValue {(0, b)} = b
Where, hom f (⊕) denotes a sequential version of ([f , ⊕]).
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

22. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
The leftwards and rightwardsfunction
Derivation by right inverse
leftwards([a] ++ x) = fold([a] ++ unfold(fold(x)))
rightwards(x ++ [a]) = fold(unfold(fold x) ++ [a]).
Now if for all xs,
rightwards xs = leftwards xs, (1)
then a list homomorphism ([f , ⊕]) that computes fold can be
obtained automatically, where f and ⊕ are defined as follows:
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

23. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
The leftwards and rightwardsfunction
Derivation by right inverse
f a = fold([a])
a ⊕ b = fold(unfold a ++ unfold b).
Equation (1) should be satisfied.
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

24. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
Programming with this homomorphism framework
MPS
A sequential program
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

25. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Automatic Parallelization
Case Study
Programming with this homomorphism framework
MPS
A tupled function
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

26. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
MPS
(mps sum) [a] = (a ↑ 0, a)
(mps sum) (x + +[a]) = let (m, s) = (mps sum) x in (m ↑ (s + a
We use this tupled function as the fold function. The right inverse
of the tupled function, (mps sum)◦:
(mps sum)◦
(m, s) = [m, s − m]
Noting that for the any result (m, s) of the tupled function the
inequality m s hold,
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

27. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
The implementation of homomorphism framework upon
Hadoop
performance tests
Environment:Hardware
COE cluster in Tokyo University which has 192 computing nodes.
We choose 16 , 8 , 4 , 2 and 1 node to run the MapReduce-MPS
program. Each node has 2 Xeon(Nocona) CPU with 2GB RAM.
Environment:Software
Linux2.6.26 ,Hadoop0.20.2 +HDFS
Hadoop configuration: heap size= 1024MB
maximum mapper pre node: 2
maximum reducer pre node: 2
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

28. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Performance
The input data
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

29. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Performance
The time consuming of calculate 100 million-long list
(SequenceFile, Pair < Long >):
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

30. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Performance
The speedup of 2-16 nodes:
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

31. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Performance
Comparison of 2 version SUM
Comparison of 2-16 nodes:
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

32. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
Performance
Conclusions
The time curve indicate the system scalability with the number of
computing nodes. The curve between x-axis 2 and 8 has biggest
slope, when the curve reaches to 16, the slope decreased, that is
because when there are more nodes, the overhead of
communication increased. Totally, the curve shows the scalability
is near-linear.
Overhead of 2 phases Map-Reduce.
Overhead of Java reflection.
Not support local reduction now (not implemented yet).
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P

33. Outline
Motivation
Brief introduction of background
The Design of Homomorphism-based Framework on MapReduce
Case Study
Performance Evaluation
The end
Questions?
?
Yu Liu A Homomorphism-based MapReduce Framework for Systematic P