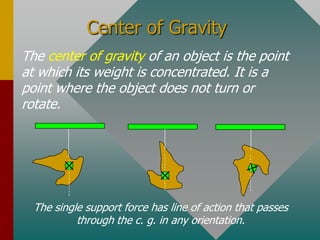
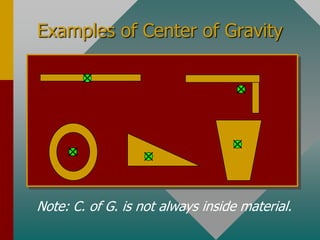
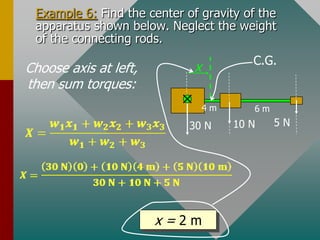
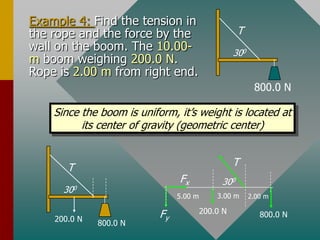
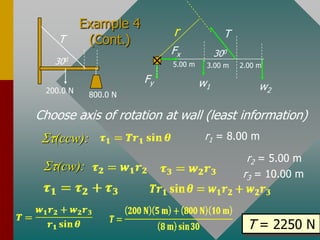
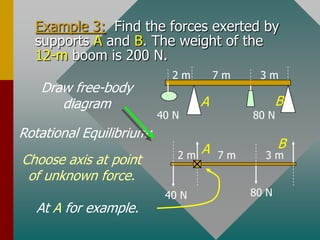
To determine if an object is in equilibrium, there can be no resultant force or torque. This means the sum of all forces and sum of all torques must equal zero. To analyze equilibrium problems, one draws a free body diagram, chooses an axis of rotation where information is lacking, sums the torques and forces about that axis, setting each sum equal to zero to solve for unknowns. Common examples involve finding tensions in ropes or forces from supports of beams or structures.

1. 05B: Equilibrium

2. San Juanico Bridge

3. Translational EquilibriumConstant speedCar at restThe linear speed is not changing with time. There is no resultant force and therefore zero acceleration. Translational equilibrium exists.

4. Constant rotationWheel at restRotational EquilibriumThe angular speed is not changing with time. There is no resultant torque and, therefore, zero change in rotational velocity. Rotational equilibrium exists.

5. First Condition:Second Condition:EquilibriumAn object is said to be in equilibrium if and only if there is no resultant force and no resultant torque.

6. SFx= 0Right = leftSFy= 0Up = downS t = 0S t (ccw)= S t (cw)ccw (+)cw (-)Total EquilibriumIn general, there are eight degrees of freedom (right, left, up, down, forward, backward, ccw, and cw):

7. General Procedure:Draw free-body diagram and label.

8. Choose axis of rotation at point where least information is given.

9. Extend line of action for forces, find moment arms, and sum torques about chosen axis:St = t1 + t2 + t3 + . . . = 0 Sum forces and set to zero: SFx= 0; SFy= 0

10. Solve for unknowns.Center of GravityThe center of gravity of an object is the point at which its weight is concentrated. It is a point where the object does not turn or rotate.The single support force has line of action that passes through the c. g. in any orientation.

11. Examples of Center of GravityNote: C. of G. is not always inside material.

12. Finding the center of gravity01. Plumb-line Method02. Principle of MomentsSt(ccw) = St(cw)

13. Example 5:Find the center of gravity of the system shown below. Neglect the weight of the connecting rods.m3 = 6.00 kgm2 = 1.00 kgSince the system is 2-D: Choose now an axis of rotation/reference axis:3.00 cmCG 2.00 cmm1 = 4.00 kgTrace in the Cartesian plane in a case that your axis of rotation is at the origin (-3.00 cm, 2.00 cm)(0, 2.00 cm)(0,0)

14. x4 m6 m5 N10 N30 NExample 6:Find the center of gravity of the apparatus shown below. Neglect the weight of the connecting rods.C.G.Choose axis at left, then sum torques:x = 2 m

15. T300800.0 NTTFx3003003.00 m5.00 m2.00 m200.0 NFy800.0 N200.0 N800.0 NExample 4: Find the tension in the rope and the force by the wall on the boom. The 10.00-mboom weighing 200.0 N. Rope is 2.00 m from right end.Since the boom is uniform, it’s weight is located at its center of gravity (geometric center)

16. Example 4 (Cont.)TTFx3003005.00 m2.00 m3.00 mFyw1w2200.0 N800.0 NrChoose axis of rotation at wall (least information)r1= 8.00 mSt(ccw):r2= 5.00 mSt(cw):r3= 10.00 mT = 2250 N

17. SF(up) = SF(down):SF(right) = SF(left):F = 1950 N, 356.3o

18. Example 3:Find the forces exerted by supports A and B. The weight of the 12-m boom is 200 N.BA2 m3 m7 m80 N40 N2 m3 m7 mDraw free-body diagramBA40 N80 NRotational Equilibrium:Choose axis at point of unknown force.At A for example.