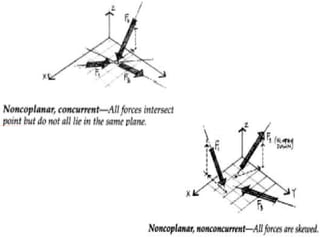
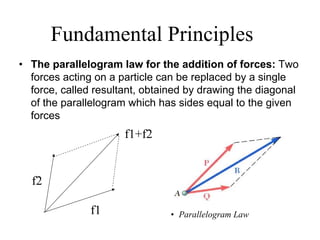
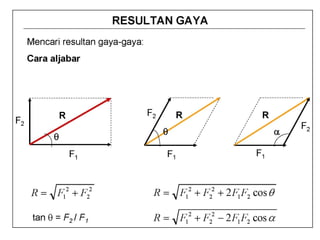
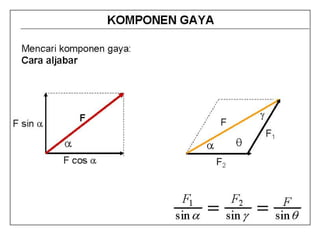
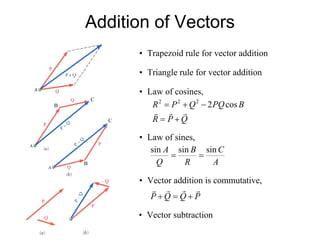
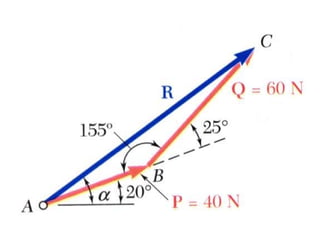
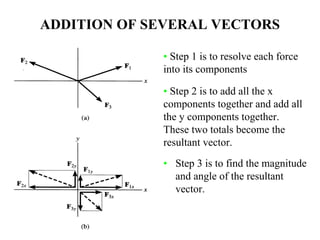
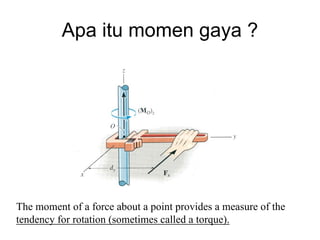
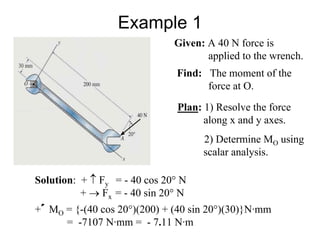
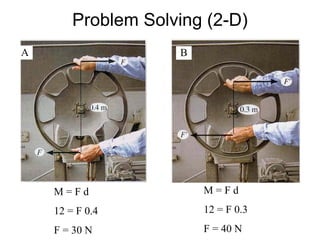
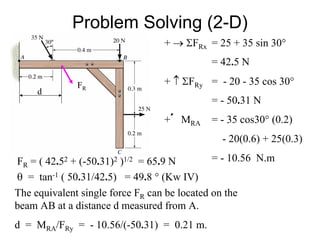
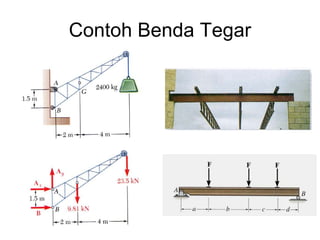
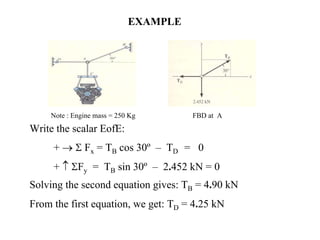
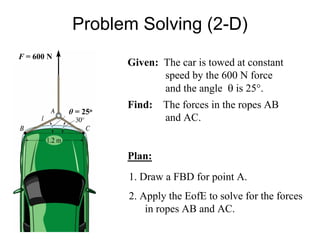
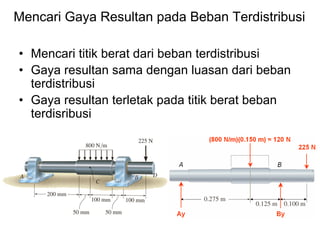
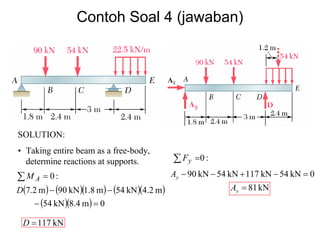
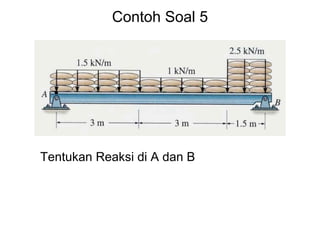
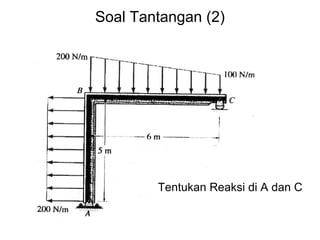
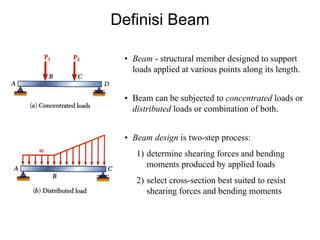
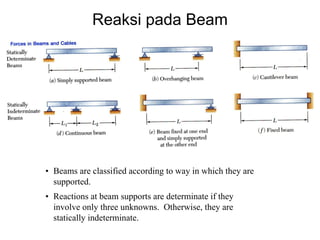
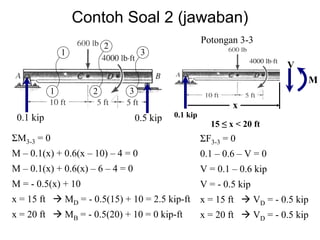
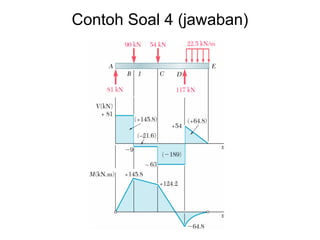
This document discusses mechanics and statics concepts such as forces, moments, and couples. It begins by defining mechanics as the branch of physics dealing with motion and forces. It then discusses rigid bodies, deformable bodies, and fluids. The document reviews the international system of units and conversions between SI and US customary units. It introduces concepts of force systems, the parallelogram law, and the principle of transmissibility. Subsequent sections cover vector addition of forces, moments of forces, moments of couples, and developing equivalent force-couple systems. Examples are provided to demonstrate solving static mechanics problems by resolving forces into components and applying principles of moments.