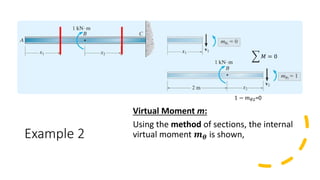
The document discusses the method of virtual work as applied to beams and frames for solving deflection and displacement problems. It outlines the processes for analyzing virtual moments and real moments using specific coordinates and provides examples for calculating vertical displacement, slope, and horizontal displacement in beam and frame structures. Key procedures include applying virtual loads, determining internal moments, and using the virtual-work equation to solve for desired outcomes.

1. CED 426
Structural Theory II
Lecture 3
Method of Virtual Work
(Beams and Frames)
Mary Joanne C. Aniñon
Instructor

2. Method of Virtual
Work: Beams and
Frames
• The method of virtual work can also
be applied to deflection problems
involving beams and frames.
• The principle of virtual work or
virtual force, may be formulated for
beam deflections by considering the
beam shown in figure (b)
• Here the displacement ∆ at point A
is to be determined

3. Method of Virtual Work: Beams and Frames
• To determine the
displacement at A, a virtual
unit load acting in the
direction of ∆ is placed on
the beam at A, and the
internal virtual moment m is
determined by method of
sections at an arbitrary
location x as shown in figure
(a)

4. Method of Virtual Work: Beams and Frames
• When the real loads act on the beam, point A is displaced ∆.
• Provided these loads cause linear elastic material response, the
element dx deforms or rotates
• On the other hand, M is the internal moment at x caused by the real
loads
• The external virtual work done by the unit load 1 ∆ and the internal
virtual work done by the moment m is md𝜃 = m(M/EI)dx.

5. Method of Virtual Work: Beams and Frames
• Summing the effects on all the elements along dx along the beam, we
can formulate the equation for virtual work

6. where,
1 = external virtual unit load acting on the beam or frame in the
direction of ∆
m = internal virtual moment in the beam or frame, expressed as a function
of x by the external virtual unit load
∆ = external displacement of the point caused by the real loads acting on the
beam or frame
M = internal moment in the beam or frame expressed as a function of x and
caused by the real loads
𝒎𝜽 = internal virtual moment in the beam or frame, expressed as a function
of x by the external virtual unit couple moment

7. Procedure for Analysis
VIRTUAL MOMENTS 𝒎 or 𝒎𝜽
• Place a unit load on the beam or frame at the point and in the direction of
the desired displacement
• If the slope is to be determined, placed a unit couple moment at the point.
• Establish appropriate x coordinates that are valid within regions of the
beam or frame where there is no discontinuity of real or virtual load
• With the virtual load in place, and all the real loads removed from the
beam or frame, calculate the internal moment 𝒎 or 𝒎𝜽 as a function of
each x coordinates
• Assume 𝒎 or 𝒎𝜽, acts in the conventional positive direction for moment

8. Procedure for Analysis
REAL MOMENTS M
• Using the same x coordinates as those established for 𝒎 or 𝒎𝜽,
determine the internal moments M caused only by the real loads.
• Since 𝒎 or 𝒎𝜽 was assumed to act in the conventional positive
direction, it is important that positive M acts in the same direction.
This is necessary since positive or negative internal work depends
upon the directional sense of the load.

9. Procedure for Analysis
VIRTUAL-WORK EQUATION
• Apply the equation of virtual work to determine the desired
displacement ∆ or rotation 𝜽. It is important to retain the algebraic
sign of each integral calculated with in its specified region.
• If the algebraic sum of all the integrals for the entire beam or frame is
positive ∆ or 𝜽 is in the same direction as the virtual unit load or
virtual unit couple, respectively. If negative value results the direction
is opposite to the unit load or couple moment.

10. Example 1
Problem:
Determine the vertical displacement at point B shown below. Take I =
71.1 x 106 mm4 and E=200 GPa.

11. Example 1
Virtual Moment m:
A vertical displacement of point B is obtained by placing a virtual load
of 1 kN at point B. Note that there are no discontinuities of loading on
the beam for both the real and virtual loads. Thus, a single x coordinate
is used.

12. Example 1
Virtual Moment m:
The x coordinate will be
selected with its origin at B,
since then the reactions at
point A do not have to be
determined in order to find
the internal moments m and
M
Using the method of sections,
the internal virtual moment m
is shown,

13. Example 1
Real Moment M:
Using the same x coordinate
and by method of sections, the
internal moment M is shown,
𝑀 = 0
𝑀 + 12𝑥
𝑥
2
= 0
𝑀 = −6𝑥2

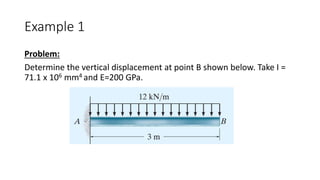
14. Example 1
• Virtual-Work Equation:
Once m and M are determined, we can now apply the virtual-work
equation to solve for the displacement at B.
0
3
6𝑥3
𝐸𝐼
𝑑𝑥 =
6 3 4
4
− [
6(0)4
4
]

15. Example 2
Problem:
Determine the slope at point B shown below. Take I = 60 x 106 mm4 and
E=200 GPa.

16. Example 2
Virtual Moment m:
The slope at B is determined by
placing a virtual couple moment of
1 kN-m at B. Here two x coordinates
must be selected in order to
determine the total virtual strain
energy in the beam. Coordinate 𝑥1
accounts for the strain energy
within segment AB and coordinate
𝑥2 accounts for that in segment BC

17. Example 2
Virtual Moment m:
Using the method of sections, the internal
virtual moment 𝒎𝜽 is shown,
𝑀 = 0
1 − 𝑚𝜃2=0

18. Example 2
Real Moments M:
Using the same coordinates 𝑥1 and 𝑥2 the
internal moments M are shown

19. Example 2
• Virtual-Work Equation:
Once 𝒎𝜽 and M are determined, we can
now apply the virtual-work equation to
solve for the slope at B.

20. Example 3
Problem:
Determine the horizontal
displacement of point C on the frame
shown below. Take E = 200 Gpa and I =
235 (106) mm4 for both members.

21. Example 3
Virtual Moments, m
• For convenience, the x1 and x2 as
shown will be used.
• A horizontal unit load is applied at C,
and the support reactions and
internal virtual moments are shown.
Type equation here.
−𝑚1 + 1 𝑥1 =0
𝑚1 = 1 𝑥1

22. Example 3
Real Moments, M
• In similar manner, the support
reactions and real moments are
shown.

23. Example 3
Virtual-Work Equation