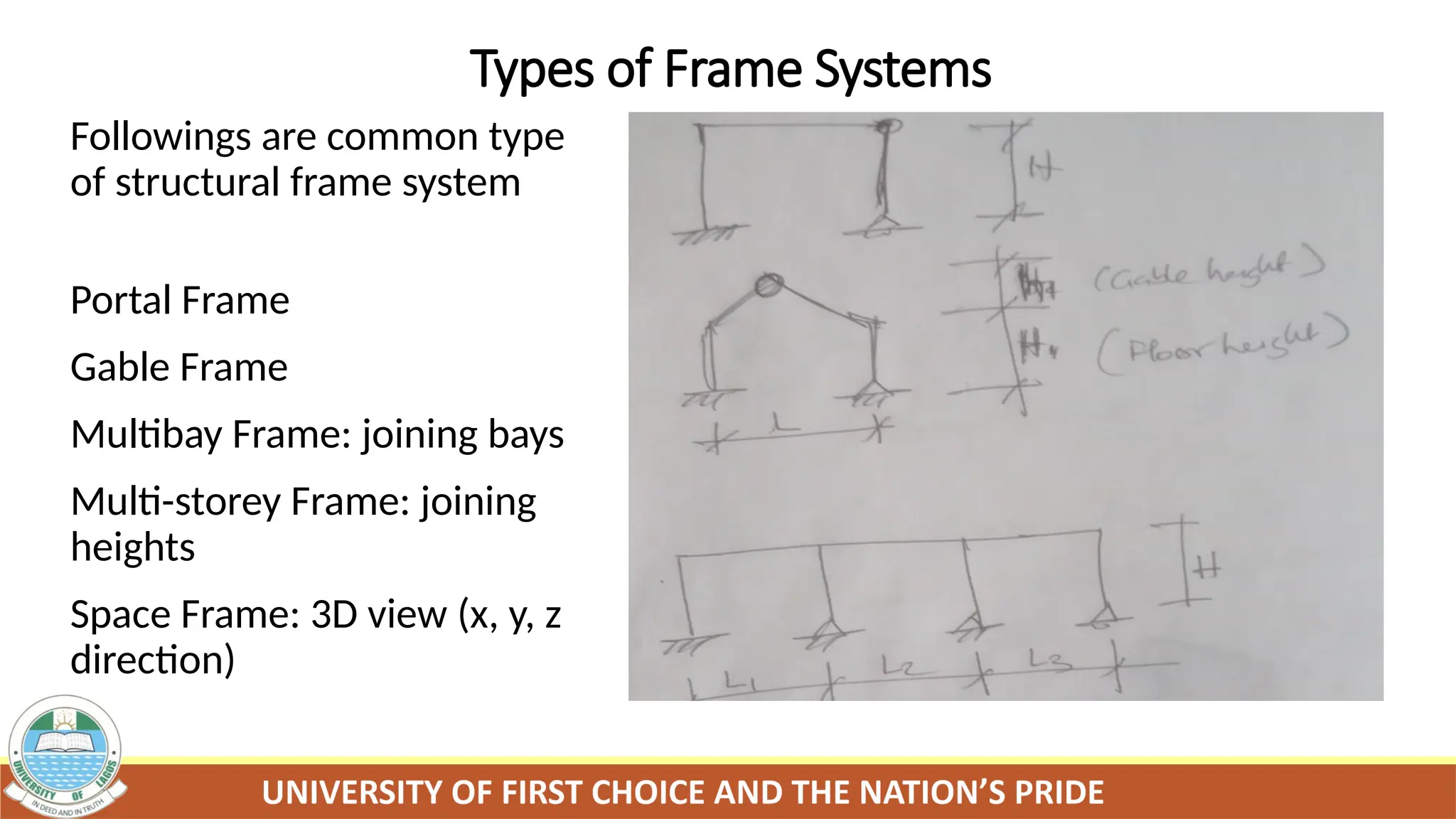
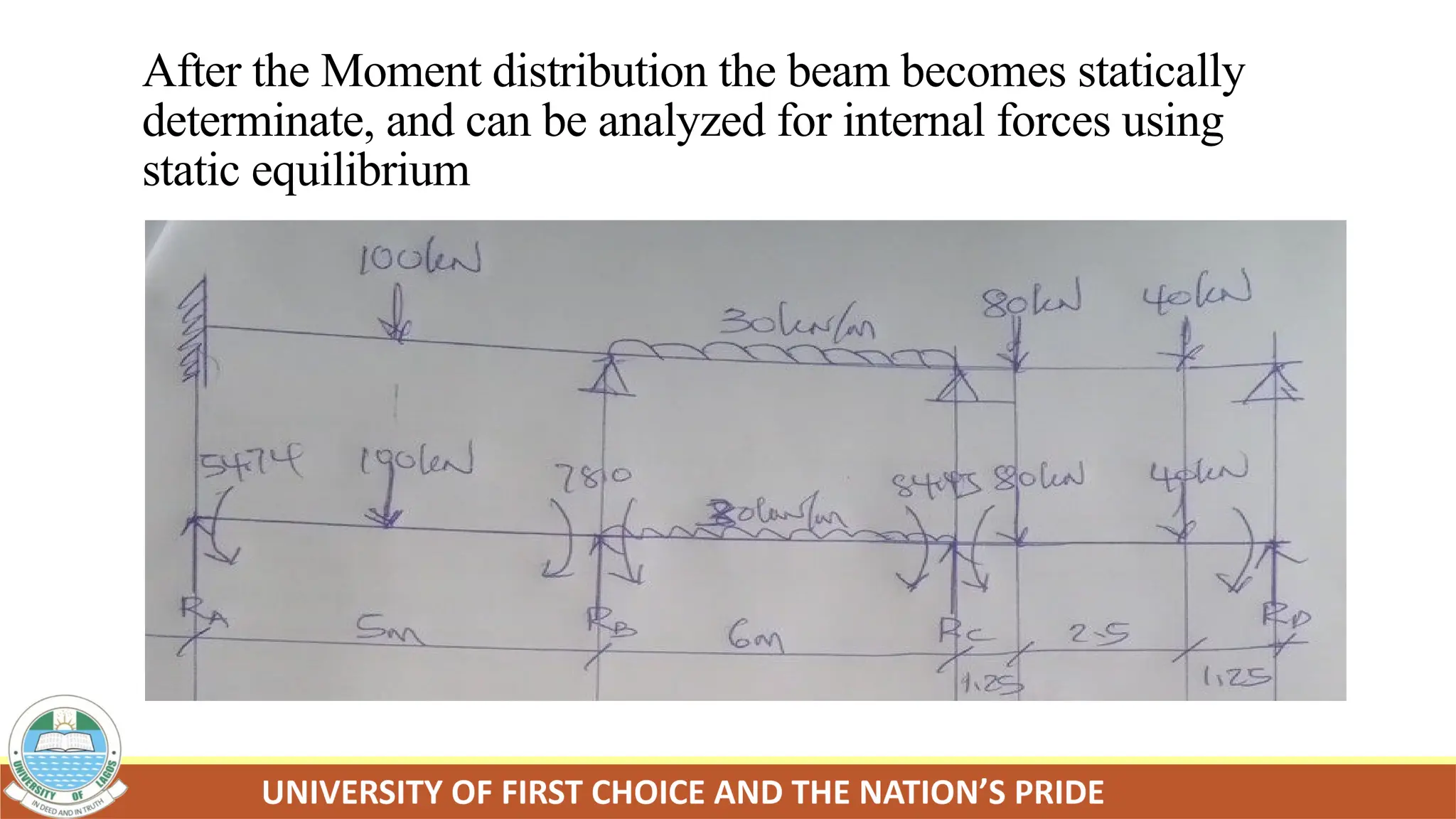
The document provides an overview of structural analysis, focusing on the evaluation of loads and structural responses necessary for design and construction in civil engineering. It covers topics such as loading systems, structural modeling, static equilibrium, methods of analysis, and distinctions between statically determinate and indeterminate structures. Additionally, it introduces both classical and modern methods for structural analysis, emphasizing the importance of algorithms and computer simulations in evaluating complex structures.