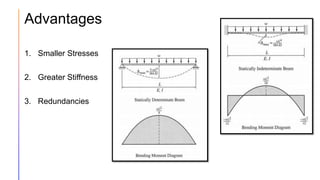
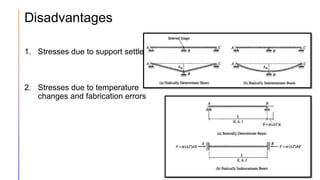
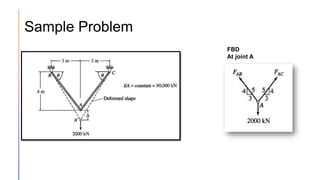
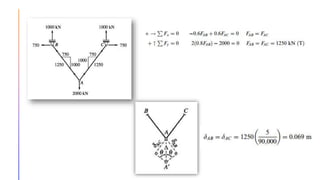
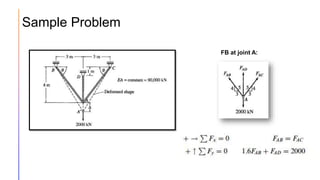
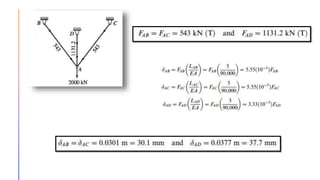
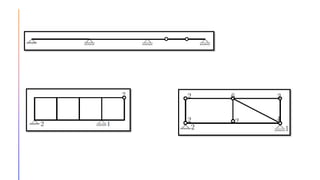
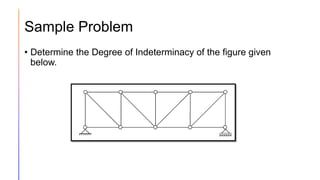
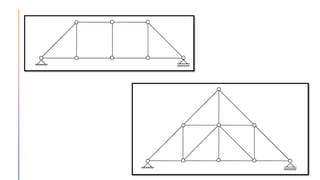
The document provides an introduction to statically indeterminate structures, highlighting the need for equilibrium equations and compatibility conditions to analyze internal forces and support reactions. It discusses advantages like smaller stresses and greater stiffness, alongside disadvantages such as sensitivity to support settlements and temperature changes. Various methods for analysis, including force and displacement methods, are outlined, alongside explanations of degrees of statical indeterminacy for beams, frames, and trusses.

1. STRUCTURAL
THEORY 2
Introduction to Statically
Indeterminate Structures
Prep by: Engr. Buluran

2. Introduction
The support reactions and internal forces of statically determinate structures can
be determined from the equations of equilibrium.
the equilibrium equations alone are not sufficient for determining the reactions and
internal forces of such structures and must be supplemented by additional
relationships based on the geometry of deformation of structures.
Compatibility conditions, ensure that the continuity of the displacements is
maintained throughout the structure and that the structure’s various parts fit
together.

3. Advantages
1. Smaller Stresses
2. Greater Stiffness
3. Redundancies

4. Disadvantages
1. Stresses due to support settlements
2. Stresses due to temperature
changes and fabrication errors

5. Analysis of
Indeterminate
Structures
• Regardless of whether a structure is
statically determinate or indeterminate, its
complete analysis requires the use of
three types of relationships:
1. Equilibrium Equations
2. Compatibility Conditions
3. Member force-deformation relations

6. Sample Problem
FBD
At joint A

8. Indeterminate Structures
In the analysis of indeterminate
structures, it is necessary to
solve the equilibrium equations
in conjunction with the
compatibility conditions of the
structure to determine its
response.
The resulting system of equations
containing only one type of unknowns
is then solved for the unknown forces
or displacements, which are then
substituted into the fundamental
relationships to determine the
remaining response of the structure

9. Sample Problem
FB at joint A:

12. Methods of Analysis
SINCE THE MID-1800S, MANY METHODS HAVE BEEN DEVELOPED FOR ANALYZING
STATICALLY INDETERMINATE STRUCTURES.
FORCE (FLEXIBILITY) METHODS DISPLACEMENT (STIFFNESS) METHODS

13. Approximate Analysis of
Rectangular Building Frames
• Force and displacement methods are exact because they satisfy
the equilibrium and compatibility of the structure.
• The preliminary designs of indeterminate structures are often
based on the result of the approximate analysis.
• Internal forces are estimated by making certain assumptions
about the deformations or the distribution of forces

14. Statical
Determinacy
Statically indeterminate
structures have more supports
or members than required for
static stability
The excess reactions and
internal forces of
indeterminate structure are
referred as Redundants.
The number of redundants is
termed as degree of
indeterminacy.

15. Degree of Statical Indeterminacy for Beams and
Frames
Where:
n = Degree of Statical Indeterminacy
s = Number of support reactions
i = Number of internal forces at hinges
m = Number of closed loops without hinge
p = number of parts

16. Sample Problem
• Determine the Degree of Indeterminacy of the figure given
below.

18. Degree of Statical Indeterminacy for Trusses
Where:
n = degree of statical indeterminacy
s = number of support reactions
m = number of truss members
nn = number of nodes

19. Sample Problem
• Determine the Degree of Indeterminacy of the figure given
below.

21. References
Structural
Analysis by
Hibbeler
Understanding
Structural
Analysis by
David Brohn