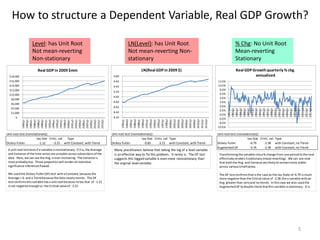
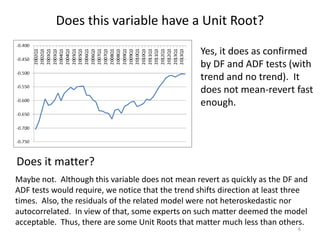
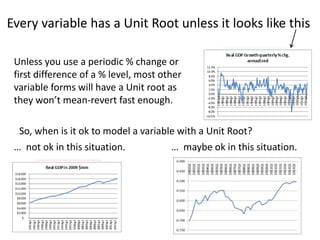
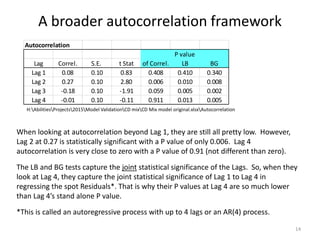
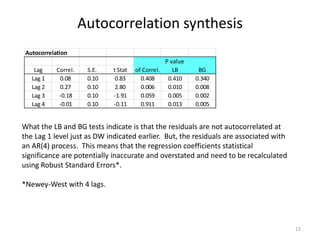
This document discusses unit roots, autocorrelation, and multicollinearity in econometric models, emphasizing the consequences of non-stationary variables. It presents methods for testing unit roots, highlighting the Dickey-Fuller tests and the importance of understanding residuals to avoid spurious regressions. Additionally, it addresses multicollinearity's effects on regression coefficients and statistical significance, offering insights on when modeling with unit root variables is acceptable.

1. Revisiting Unit Root, Autocorrelation
and Multicollinearity
Gaetan Lion
July 2015
revised and expanded vs. earlier version
1

2. Unit Root
2

3. Unit Root basics
A Unit Root is a problem that occurs when the best estimate of Y is
Y t-1, and that coefficient* is very close to 1 or higher (or lower).
This denotes a Y variable that is non-stationary and does not
mean-revert (or not mean-revert fast enough).
The average and the variance of Y are unstable.
In such a situation, you will get “spurious” regression results with
high R^2, high t-stat, and often Durbin Watson < 1 (high
autocorrelation) but no economic meaning.
If you detrend Y, the resulting Goodness-of-fit of detrended
estimates and performance in Hold Out could be really poor.
3
*Y = b Y t-1

4. How to test for Unit Root?
You use the Dickey-Fuller (DF) test or the Augmented
Dickey-Fuller (ADF) test.
DF test: Regress Chg. in Y using just Y t-1 (Lag 1) as an
independent variable.
ADF: add to the ind. variables: Chg. in Y t-1, or more lags.
Those simple regressions come with discretionary
decisions. If Y does trend, you add a trend variable (1, 2,
3, …). If average of Y is not very different from 0, you
don’t use an Intercept.
4

5. How to structure a Dependent Variable, Real GDP Growth?
5
Unit root test (nonstationary): Unit root test (nonstationary): Unit root test (nonstationary):
tau Stat Critic. val. Type tau Stat Critic. val. Type tau Stat Critic. val. Type
Dickey-Fuller -1.12 -3.15 with Constant, with Trend Dickey-Fuller -0.83 -3.15 with Constant, with Trend Dickey-Fuller -6.79 -2.58 with Constant, no Trend
Augmented DF -4.74 -2.58 with Constant, no Trend
$-
$2,000
$4,000
$6,000
$8,000
$10,000
$12,000
$14,000
$16,000
$18,000
1982q1
1983q3
1985q1
1986q3
1988q1
1989q3
1991q1
1992q3
1994q1
1995q3
1997q1
1998q3
2000q1
2001q3
2003q1
2004q3
2006q1
2007q3
2009q1
2010q3
2012q1
2013q3
Real GDP in 2009 $mm
8.20
8.40
8.60
8.80
9.00
9.20
9.40
9.60
9.80
1982q1
1983q3
1985q1
1986q3
1988q1
1989q3
1991q1
1992q3
1994q1
1995q3
1997q1
1998q3
2000q1
2001q3
2003q1
2004q3
2006q1
2007q3
2009q1
2010q3
2012q1
2013q3
LN(Real GDP in2009 $)
-10.0%
-8.0%
-6.0%
-4.0%
-2.0%
0.0%
2.0%
4.0%
6.0%
8.0%
10.0%
12.0%
1982q1
1983q3
1985q1
1986q3
1988q1
1989q3
1991q1
1992q3
1994q1
1995q3
1997q1
1998q3
2000q1
2001q3
2003q1
2004q3
2006q1
2007q3
2009q1
2010q3
2012q1
2013q3
Real GDP Growthquarterly % chg.
annualized
A unitroot testtestsif a variable isnonstationary. If itis,the Average
and Variance of the time seriesare unstable acrosssubsectionsof the
data. Here,we can see the Avg.iseverincreasing. The Variance is
mostprobablytoo. Those propertieswill renderall statistical
significance inferencesflawed.
We usedthe Dickey-Fuller(DF) test withaConstant,because the
Average > 0, and a Trendbecause the data clearlytrends. The DF
testconfirmsthisvariable hasa unitrootbecause itstau Stat of -1.12
isnot negative enoughvs.the Critical valueof - 3.15.
Many practitioners believe that taking the log of a level variable
is an effective way to fix this problem. It rarely is. The DF test
suggests this logged variable is even more nonstationary than
the original level variable.
Transformingthe variable intoa% change from one periodtothe next
effectivelyrendersitstationary(mean-reverting). We can see now
that boththe Avg. andVariance are likelytoremainmore stable
across varioustimeframes.
The DF testconfirmsthatisthe case as the tau State of-6.79 ismuch
more negative thanthe Critical value of- 2.58 (fora variable withan
Avg. greaterthan zeroand notrend). In thiscase we also usedthe
AugmentedDFtodouble checkthatthisvariable isstationary. It is.
Level: has Unit Root
Not mean-reverting
Non-stationary
LN(Level): has Unit Root
Not mean-reverting Non-
stationary
% Chg: No Unit Root
Mean-reverting
Stationary

6. Does this variable have a Unit Root?
6
Yes, it does as confirmed
by DF and ADF tests (with
trend and no trend). It
does not mean-revert fast
enough.
Does it matter?
Maybe not. Although this variable does not mean revert as quickly as the DF and
ADF tests would require, we notice that the trend shifts direction at least three
times. Also, the residuals of the related model were not heteroskedastic nor
autocorrelated. In view of that, some experts on such matter deemed the model
acceptable. Thus, there are some Unit Roots that matter much less than others.

7. Every variable has a Unit Root unless it looks like this
7
Unless you use a periodic % change or
first difference of a % level, most other
variable forms will have a Unit root as
they won’t mean-revert fast enough.
So, when is it ok to model a variable with a Unit Root?
… maybe ok in this situation.… not ok in this situation.

8. When is a Unit Root acceptable?
8
After pondering this question for months, I have uncovered an
easy answer.
Models with unit root variables are fine when their residuals do
not have a unit root (stationary). In such a situation, the
dependent variable with a unit root is deemed to be cointegrated
(have a stable relationship) with one or more of the independent
variables. In such case, you have a Cointegration model. And,
the resulting regression is not spurious and not absent of any
economic meaning as spurious regressions that are not
cointegrated.
Reference: Engle & Granger “Cointegration and error correction: Representation,
estimation and testing.” (1987)

9. When to consider Cointegration Models
9
• When detrending the variable anymore appears to generate
more noise regarding the relationship between variables;
• The variables with Unit Root are constrained. Thus, they do not
grow forever. Examples include unemployment rate, interest
rates, and all variables constrained between 0 and 1. Such
variables often have a unit root because their time series is too
short to capture their mean reverting property;
• The regression model’s residuals are associated with no more
than a moderate autocorrelation. A DW score < 1.00 may be
deemed too low;
• The residuals tests well for stationarity. That’s the definition of
a Cointegration model.

10. Unit Root testing revisited
10
The DF and ADF tests are helpful in diagnosing a Unit
Root. And, they are helpful in diagnosing the potential
absence of Unit Root in the residuals. But, a more
appropriate test for testing whether the residuals are
stationary is Phillips-Ouliaris. In such a situation
(residuals stationary), your model is a Cointegration
Model. And, you have overcome the issues with Unit
Root and “spurious” regressions.
The term “spurious” is quoted from Granger & Newbold “Spurious regressions in
econometrics” (1974).

11. Autocorrelation
11

12. Autocorrelation Quiz
12
A model’s residuals have a Durbin Watson score of 1.83
(excellent score denoting no autocorrelation) and an actual
autocorrelation very close to Zero at 0.08.
Are the above residuals indeed not autocorrelated?
The Question is the Answer, as they say…

13. Durbin Watson is outdated
13
You still have to calculate it because everyone still uses it including
SAS, STATA, EViews, etc…
Why is it outdated:
1) It is highly imprecise associated with a large range of
uncertainty (as defined in DW tables);
2) It can’t handle a model with autoregressive variables (Y t-1,
etc…);
3) It can’t measure autocorrelation for other lags (t-1, t-2, etc…).
DW is being replaced by the Ljung-Box (LB) and Breusch-Godfrey
(BG) tests that can handle all three situations mentioned above.

14. A broader autocorrelation framework
14
Autocorrelation
P value
Lag Correl. S.E. t Stat of Correl. LB BG
Lag 1 0.08 0.10 0.83 0.408 0.410 0.340
Lag 2 0.27 0.10 2.80 0.006 0.010 0.008
Lag 3 -0.18 0.10 -1.91 0.059 0.005 0.002
Lag 4 -0.01 0.10 -0.11 0.911 0.013 0.005
H:AbilitiesProjects2015Model ValidationCD mixCD Mix model original.xlsxAutocorrelation
When looking at autocorrelation beyond Lag 1, they are still all pretty low. However,
Lag 2 at 0.27 is statistically significant with a P value of only 0.006. Lag 4
autocorrelation is very close to zero with a P value of 0.91 (not different than zero).
The LB and BG tests capture the joint statistical significance of the Lags. So, when they
look at Lag 4, they capture the joint statistical significance of Lag 1 to Lag 4 in
regressing the spot Residuals*. That is why their P values at Lag 4 are so much lower
than Lag 4’s stand alone P value.
*This is called an autoregressive process with up to 4 lags or an AR(4) process.

15. Autocorrelation synthesis
15
Autocorrelation
P value
Lag Correl. S.E. t Stat of Correl. LB BG
Lag 1 0.08 0.10 0.83 0.408 0.410 0.340
Lag 2 0.27 0.10 2.80 0.006 0.010 0.008
Lag 3 -0.18 0.10 -1.91 0.059 0.005 0.002
Lag 4 -0.01 0.10 -0.11 0.911 0.013 0.005
What the LB and BG tests indicate is that the residuals are not autocorrelated at
the Lag 1 level just as DW indicated earlier. But, the residuals are associated with
an AR(4) process. This means that the regression coefficients statistical
significance are potentially inaccurate and overstated and need to be recalculated
using Robust Standard Errors*.
*Newey-West with 4 lags.

16. Implication
16
If the reviewed model (with very low autocorrelations) was
deemed to have autocorrelated residuals up to 4 Lags, as specified
earlier, one can imagine that the majority of time series models will
have autocorrelated residuals. Get used to calculating Newey-West
Standard Errors on most time-series regression models.
SAS, EViews, STATA routinely
generate Correlograms studying
autocorrelations up to 15 to 36 lags
as a default. The Q-Stat shown is the
Ljung-Box score. Notice how it goes
up the more lags you use. And, the P
value is Zero… meaning this data
series is very autocorrelated.

17. Multicollinearity
17

18. Multicollinearity: The main issues
18
1) Regression coefficients will have much larger standard errors
and lower statistical significance than otherwise;
2) As the R^2 of the regression model testing for multicollinearity
approaches 1, 1 – R^2 approaches 0. At some point, this
renders the inversion of the underlying matrix calculation
between unstable to impossible as a quantity divided by 0 is
undefined;
3) Potentially, large changes in regression coefficients when the
multicollinear variable is removed.

19. The Basic Multicollinearity Framework
19
H:AbilitiesProjects2015EconometricsReg Model testing.xlsxMulticollinearity
VIF = 1/(1 – R^2)
Calculation Measure Parameter
R 0.95
R^2 R Square 0.90
1 - R^2 Tolerance 0.10
1/Tolerance VIF 10
VIF = Variance Inflation Factor.

20. An Emerging New Standard: SQRT(VIF) = 2
20
Calculation Measure Parameter
R 0.87
R^2 R Square 0.75
1 - R^2 Tolerance 0.25
1/Tolerance VIF 4
SQRT(VIF) 2
H:AbilitiesProjects2015EconometricsReg Model testing.xlsxMulticollinearity
Source: John Fox 1991, 2011
The SQRT(VIF) of 2 means that the Standard Error of the regression coefficient
being tested is twice as high than if the independent variable was not
multicollinear at all.
You could calculate the SQRT(VIF) by dividing the Standard Error of the reg.
coefficient within your multiple regression by the one in a linear regression
using this only one independent variable.

21. Does SQRT(VIF) = 2 matters?
21
It mainly matters if you are concerned about a TYPE II Error…
rejecting an independent variable because of lack of statistical
significance (accepting the null hypothesis that the regression
coefficient is not different from zero).
If tested variable is already stat. significant, SQRT(VIF) = 2 is not
much of a concern.

22. Does VIF = 10 matters?
22
The answer is the same as for SQRT(VIF) = 2. VIF = 10 translates
into boosting the Standard Error of the tested regression
coefficient by 3.3 times. But, if the coefficient is already stat.
significant this is not an issue.
How about the associated R^2 of 0.90 being close to
destabilizing the calculations of inverting a matrix to resolve the
original regression?
Any software algorithm can easily divide by 0.10. That’s not a
problem. To be threatening, the R Square must be closer to
something like 0.999… This in turn means that Correlation must
be even closer to 1. Maybe VIF = 1,000,000 would be a
problem… but not VIF = 10.

23. How about the change in regression coefficients
when you remove a variable? It depends…
23
Let’s say you regress GNP growth as follows:
GNP = Const. + b1 S&P 500 + b2 Home price + b3 FF + b4 LIBOR
The regression coefficients for FF and LIBOR are both -0.10. You
remove FF. LIBOR’s coefficient moves to -0.20 and the other two
coefficients (Stock and Home prices) do not move much. Is that a
problem? Probably not…
On the other hand, if they did move a lot that may be a problem.
And, the weaker rate variable should probably be removed.
However, neither VIF = 10 nor SQRT(VIF) = 2 will give you any
indication in what situation you are in. You’ll just have to try it
out.