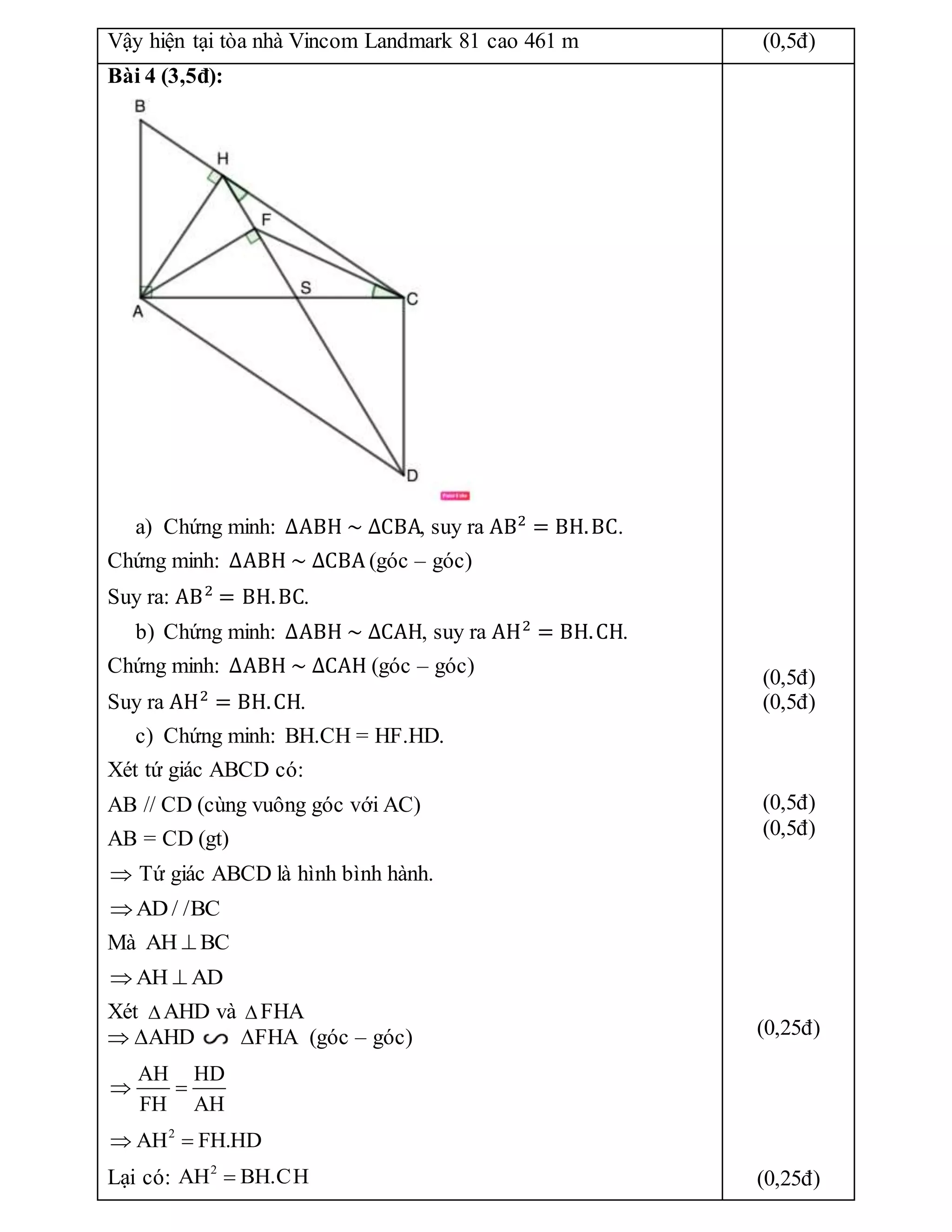
The document contains 5 math problems: 1) Solving various equations and inequalities. 2) Graphing the solutions of two inequalities on a number line. 3) Using an equation to calculate the length of a road based on time and speed information. 4) Using similar triangles to calculate the height of a building based on shadow lengths. 5) Proving several properties about angles and lengths in similar right triangles.

1. Bài 1: (3,0 điểm) Giải các phương trình sau:
a) 3x+ 2 = 5x+ 12
b) (x− 2)(2x+ 3) = 0
c)
9x−12
15
+
x
6
=
x+1
2
d)
x+7
x−4
−
7
x+4
=
𝑥2
+56
𝑥2−16
Bài 2: (1,5 điểm) Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 5x − 3 ≤ 8x − 2
b)
3+2x
4
−
1+3x
6
>
6−x
12
Bài 3: (1,0 điểm)
Một ô tô chạy trên quãng đường AB. Lúc đi ô tô chạy với
vận tốc 50 km/h. Lúc về ô tô chạy với vận tốc 40 km/h
nên thời gian về nhiều hơn thời gian đi là 36 phút. Tính
chiều dài quãng đường AB?
Bài 4: (1,0 điểm)
Toànhà Vincom Landmark 81 cao 81 tầng nằm trong khu
đô thị Vinhomes Central Park. Bóng của toà nhà trên mặt
đất dài 57,625m. Cùng thời điểm đó, một thanh sắt cao
1,6m cắm vuông góc với mặt đất có bóng dài 0,2m. Tính
chiều cao tòa nhà Vincom Landmark 81?
Bài 5: (3,5 điểm)
Cho ∆ABC vuông tại A (AB < AC), có đường cao AH.
a) Chứng minh: ∆ABH ∼ ∆CBA, suy ra AB2
= BH.BC.
b) Chứng minh: ∆ABH ∼ ∆CAH, suy ra AH2
= BH.CH.
c) Trên đường thẳng vuông góc với AC tại C, lấy điểm D sao cho CD = AB (D và
B nằm khác phía so với đường thẳng AC). HD cắt AC tại S. Kẻ AF ⊥ HS tại F.
Chứng minh: BH.CH = HF.HD.
d) Chứng minh: SCF
̂ = SHC
̂ .
Hết
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 2
TRƯỜNG THCS GIỒNG ÔNG TỐ
ĐỀ KIỂM TRA HỌC KỲ II
Năm học: 2019 - 2020
Môn: Toán – Lớp 8
Thời gian làm bài: 90 phút
(Không kể thời gian giao đề)
ĐỀ CHÍNH THỨC

2. NỘI DUNG ĐIỂM
Bài 1: Giải phương trình 3 điểm
a) 3x + 2 = 5x+ 12
<=> 3x – 5x = 12 – 2
<=> -2x = 10
<=> x = -5
Vậy S = {-5}
b) (x− 2)(2x+ 3) = 0
<=> x – 2 = 0 hay 2x + 3 = 0
<=> x = 2 hay x =
−3
2
Vậy S = {2;
−3
2
}
c)
9x−12
15
+
x
6
=
x+1
2
<=>
2(9x−12)
30
+
5x
30
=
15(x+1)
30
<=> 18x – 24 + 5x = 15x + 15
<=> 8x = 39
<=> x =
39
8
Vậy S = {
39
8
}
d)
x+7
x−4
−
7
x+4
=
𝑥2
+56
𝑥2−16
ĐKXĐ: x ≠ 4 và x ≠ -4
<=>
(x+7)(x+4)
(x−4)(x+4)
−
7(x−4)
(x−4)(x+4)
=
𝑥2
+56
(x−4)(x+4)
=> 𝑥2
+ 4x + 7x + 28 – 7x + 28 = 𝑥2
+ 56
<=> 4x = 0
<=> x = 0 (N)
Vậy S = {0}
0,75 đ
(0,25đ x 3)
0,75 đ
(0,25đ)
(0,25đ x 2)
0,75đ
(0,25đ)
(0,25đ)
(0,25đ)
0,75đ
(0,25đ)
(0,25đ)
(0,25đ)
Bài2: Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục
số:
1,5đ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 2
TRƯỜNG THCS GIỒNG ÔNG TỐ
ĐÁP ÁN KIỂM TRA HỌC KỲ II
Năm học: 2019-2020
MÔN: TOÁN 8 ( đề chính thức)

3. a) 5x − 3 ≤ 8x − 2
<=> -3x ≤ 1
<=> x ≥ −1/3
Vậy S = { x| x ≥ −1/3}
b)
3+2x
4
−
1+3x
6
>
6−x
12
<=>
3(3+2x)
12
−
2(1+3x)
12
>
6−x
12
<=> 3(3+ 2x) − 2(1+ 3x) > 6 − x
<=> 9 + 6x − 2 − 6x > 6 − x
<=> x > −1
Vậy S = { x| x > −1}
0,75đ
(0,25đ x2)
(0,25đ)
0,75đ
(0,25đ)
(0,25đ)
(0,25đ)
Bài 3:
36 phút =
36
60
=
3
5
(h)
Gọi x (km) là chiều dài quãng đường AB (x > 0)
Thời gian lúc đi là:
x
50
(h)
Thời gian lúc về là:
x
40
(h)
Vì thời gian về nhiều hơn thời gian đi là 36 phút nên ta có phương
trình:
𝑥
40
−
𝑥
50
=
3
5
<=> x = 120 (N)
Vậy quãng đường AB dài 120km.
1,0đ
(0,25đ)
(0,25đ)
(0,5đ)
Bài 4:
Vì tia nắng có tính chất song song nên BC // B’C’
Chứng minh được hai tam giác ABC và A’B’C’ đồng dạng
Lập tỉ số đồng dạng tính AB = 461
1,0đ
(0,25đ)
(0,25đ)

4. Vậy hiện tại tòa nhà Vincom Landmark 81 cao 461 m (0,5đ)
Bài 4 (3,5đ):
a) Chứng minh: ∆ABH ∼ ∆CBA, suy ra AB2
= BH.BC.
Chứng minh: ∆ABH ∼ ∆CBA (góc – góc)
Suy ra: AB2
= BH.BC.
b) Chứng minh: ∆ABH ∼ ∆CAH, suy ra AH2
= BH.CH.
Chứng minh: ∆ABH ∼ ∆CAH (góc – góc)
Suy ra AH2
= BH.CH.
c) Chứng minh: BH.CH = HF.HD.
Xét tứ giác ABCD có:
AB // CD (cùng vuông góc với AC)
AB = CD (gt)
 Tứ giác ABCD là hình bình hành.
AD / /BC

Mà AH BC

AH AD
 
Xét AHD và FHA
 AHD FHA (góc – góc)
AH HD
FH AH
 
2
AH FH.HD
 
Lại có: 2
AH BH.CH

(0,5đ)
(0,5đ)
(0,5đ)
(0,5đ)
(0,25đ)
(0,25đ)

5. Nên: BH. CH= FH. HD
d) Chứng minh: SCF
̂ = SHC
̂ .
Chứng minh: ASF DSC (g.g)
Chứng minh: ASD FSC (c.g.c) => ADS
̂ = SCF
̂
Mà ADS
̂ = SHC
̂ (hai góc sole trong, AD // BC) => SCF
̂ = SHC
̂
Lưu ý:
Học sinh không vẽ hình, không chấm tự luận. Vẽ hình đến câu nào
chấm đến câu đó.
Học sinh có thể dùng cách khác để chứng mình, giám khảo căn cứ
thang điểm mà chấm.
(0,25đ)
(0,75đ)
Làm trọn
câu được
0,75 điểm,
không chấm
bước.