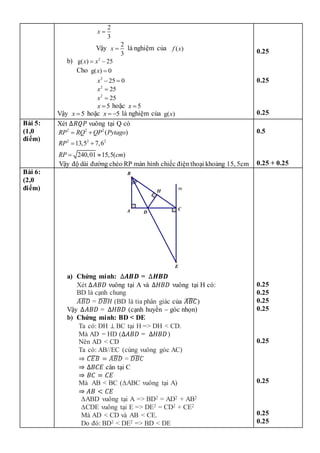
1. The document contains a math test for 7th grade students with 6 questions. 2. Question 1 involves calculating the average test score for 20 students in math class. Question 2 asks students to draw a line graph representing workforce data. 3. Question 3 involves simplifying algebraic expressions, evaluating them for given values, and adding and subtracting polynomials. 4. The remaining questions involve finding solutions to equations, calculating the hypotenuse of a right triangle, and proving properties of triangles.

1. ỦY BAN NHÂN DÂN
HUYỆN HÓC MÔN
TRƯỜNG THCS TÔ KÝ
KIỂM TRA HỌC KỲ II KHỐI LỚP 7
NĂM HỌC 2019 – 2020
MÔN: TOÁN HỌC
Thời gian: 90 phút
Bài1 (1,5 điểm). Điểm kiểm tra môn Toáncủa 20 học sinh lớp 7A được ghi lại như sau:
5 9 4 8 7 6 7 10 7 7
8 6 5 9 5 7 10 9 8 7
a) Hãy lập bảng tần số
b) Tính điểm trung bình môn Toán của 20 học sinh trên.
Bài 2 (1,5 điểm). Số năm làm việc của một số công nhân trong một phân xưởng được
ghi lại như sau:
Giá trị (x) 5 7 8 9 10
Tần số (n) 4 2 5 6 8
Dựa vào bảng trên, em hãy vẽ biểu đồ đoạn thẳng mô tả bảng dữ liệu này.
Bài 3 (3,0 điểm). Cho đơn thức 2 2 2
1
A ( x y ).(6xy )
3
 
và 2 đa thức 2
M(x) 2x x 3
    và 2
N(x) 3x 5x 7
  
a) Thu gọn đơn thức A
b) Tính giá trị của A tại
1
x
2
 và y 2
 
c) Tính M(x) N(x)
 và M(x) N(x)

Bài 4 (1,0 điểm). Tìmnghiệm các đa thức sau:
a) f (x) 3x 2
 
b) 2
g(x) x 25
 
Bài5 (1,0 điểm). Hình bên là chiếc điện thoại Samsung S10.
Biết chiều dài QR củachiếc điện thoại là 13,5 cm, chiều rộng
QP là 7,6 cm. Hỏi độ dài đường chéo RP của màn hình chiếc
điện thoại là bao nhiêu cm? (Làm tròn kết quả đến chữ số
thập phân thứ nhất)
Bài6 (2,0 điểm). Cho ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Vẽ
DH vuông góc với BC tại H.
a) Chứng minh: ABD = HBD.
b) Qua C vẽ đường thẳng m vuông góc với AC. Đường thẳng m cắt tia BD tại E.
Chứng minh: BD < DE
HẾT
ĐỀ CHÍNH THỨC

2. ỦY BAN NHÂN DÂN
HUYỆN HÓC MÔN
TRƯỜNG THCS TÔ KÝ
HƯỚNG DẪN CHẤM HỌC KỲ II
KHỐI LỚP 7 NĂM HỌC 2019 – 2020
MÔN: TOÁN HỌC
Thời gian: 90 phút
Bài 1
(1,5
điểm)
a)
Điểm số (x) 4 5 6 7 8 9 10
Số học sinh (n) 1 3 2 6 3 3 2 N = 20
b) Điểm trung bình của 20 học sinh là
4.1 5.3 6.2 7.6 8.3 9.3 10.2
7,2
20
X
     
 
Bảng tầng số
(1 điểm) – sai
hoặc thiều 1
tần số hoặc 1
giá trị trừ
0,25đ
0.25đ+0.25đ
Bài 2:
(1,5
điểm)
HS vẽ sai một giá
trị trừ 0,25. Sai từ
3 giá trị trở lên
không tính điểm
Bài 3:
(3,0
điểm)
a) 2 2 2
1
( ).(6 )
3
A x y xy
 
2 2 2
1
.6. .
3
A x x y y
 
3 4
2
A x y
 
b) Thay
1
2
x  và 2
y   vào A ta có:
 
3
4
1
2 2 4
2
A
 
    
 
 
c)
2
2
2
( ) 2 3
N( ) 3 5 7
( ) ( ) 6 10
M x x x
x x x
M x N x x x
   
  
   
2
2
2
( ) 2 3
N( ) 3 5 7
( ) ( ) 5 4 4
M x x x
x x x
M x N x x x
   
  
   
0.25
0.25
0.25
0.25x3
0.25x3
0.25x3
Bài 4:
(1,0
điểm)
a) ( ) 3 2
f x x
 
Cho ( ) 0
f x 
3 2 0
x  0.25
n
x
8
6
5
4
2
1
10
9
8
7
5
1
HDC CHÍNH THỨC

3. 2
3
x 
Vậy
2
3
x  là nghiệm của ( )
f x
b) 2
g( ) 25
x x
 
Cho g( ) 0
x 
2
25 0
x  
2
25
x 
2
25
x 
5
x  hoặc 5
x 
Vậy 5
x  hoặc 5
x   là nghiệm của g( )
x
0.25
0.25
0.25
Bài 5:
(1,0
điểm)
Xét ∆𝑅𝑄𝑃 vuông tại Q có
2 2 2
2 2 2
( )
13,5 7,6
240,01 15,5( )
RP RQ QP Pytago
RP
RP cm
 
 
 
Vậy độ dài đường chéo RP màn hình chiếc điện thoại khoảng 15, 5cm
0.5
0.25 + 0.25
Bài 6:
(2,0
điểm)
a) Chứng minh: ∆𝑨𝑩𝑫 = ∆𝑯𝑩𝑫
Xét ∆𝐴𝐵𝐷 vuông tại A và ∆𝐻𝐵𝐷 vuông tại H có:
BD là cạnh chung
𝐴𝐵𝐷
̂ = 𝐷𝐵𝐻
̂ (BD là tia phân giác của 𝐴𝐵𝐶
̂)
Vậy ∆𝐴𝐵𝐷 = ∆𝐻𝐵𝐷 (cạnh huyền – góc nhọn)
b) Chứng minh: BD < DE
Ta có: DH ⊥ BC tại H => DH < CD.
Mà AD = HD (∆𝐴𝐵𝐷 = ∆𝐻𝐵𝐷)
Nên AD < CD
Ta có: AB//EC (cùng vuông góc AC)
⇒ 𝐶𝐸𝐵
̂ = 𝐴𝐵𝐷
̂ = 𝐷𝐵𝐶
̂
⇒ ∆𝐵𝐶𝐸 cân tại C
⇒ 𝐵𝐶 = 𝐶𝐸
Mà AB < BC (∆ABC vuông tại A)
⇒ 𝐴𝐵 < 𝐶𝐸
∆ABD vuông tại A => BD2 = AD2 + AB2
∆CDE vuông tại E => DE2 = CD2 + CE2
Mà AD < CD và AB < CE.
Do đó: BD2 < DE2 => BD < DE
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
m
E
H
D
A C
B