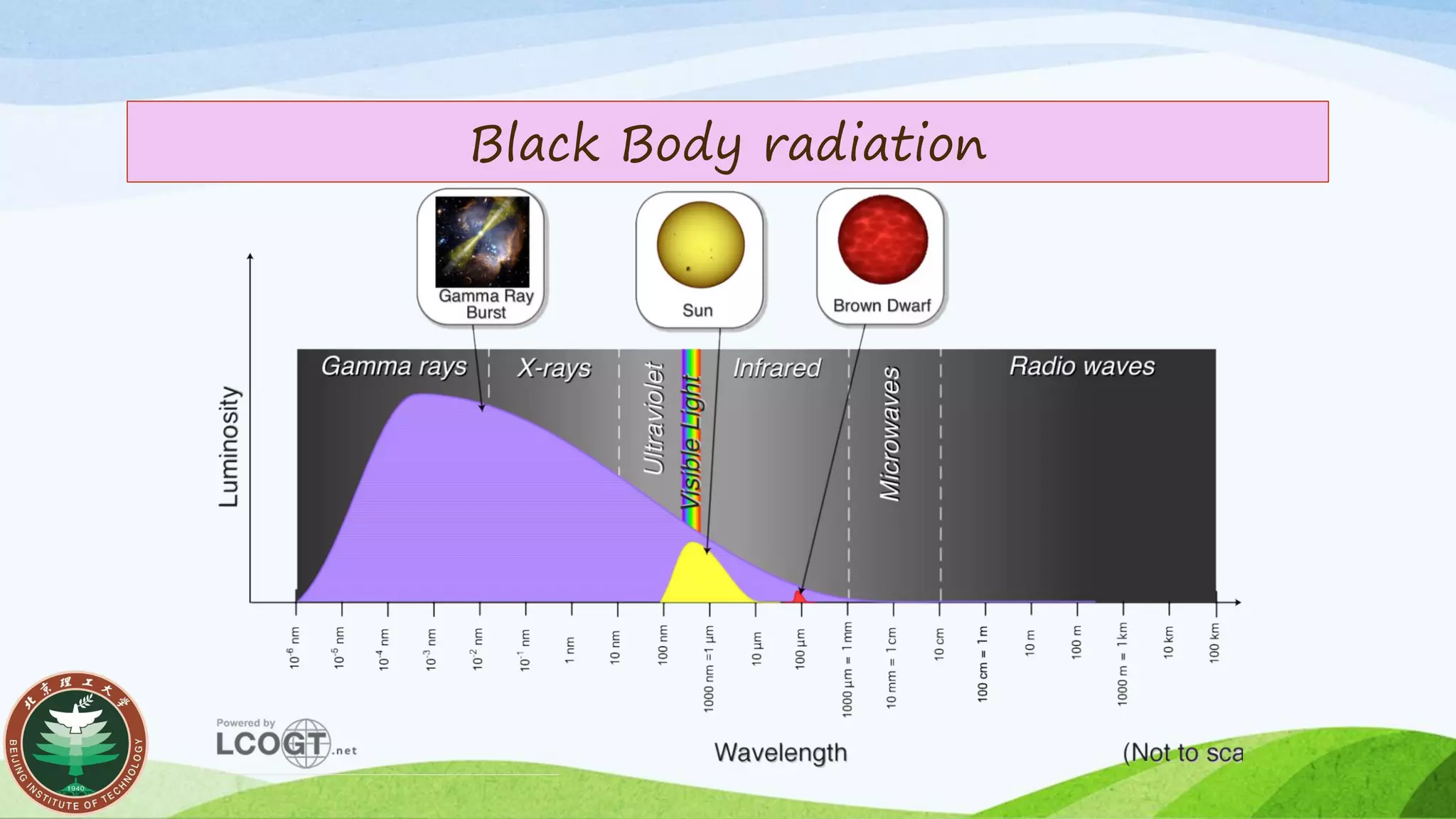
Thermal radiation is emitted by all objects due to the vibrational and rotational movements of molecules and atoms. It is transported via electromagnetic waves and can propagate through a vacuum. All objects emit radiation at any temperature above absolute zero according to their emissivity. Blackbody radiation follows Planck's law, with a continuous frequency spectrum that depends only on temperature. It has a peak wavelength defined by Wien's displacement law. The total power output of blackbody radiation is described by Stefan-Boltzmann law. The view factor is used to account for incomplete radiation exchange between surfaces, describing the fraction of radiation leaving one surface that is received by another. It is essential for calculating radiation heat transfer between surfaces.

1. Thermal Radiation
Beijing Institute of Technology
Group – ‘9’

2. Presenters
普拉赛(Nepal)
2820170058
比拉(Pakistan)
2820166036

3. Thermal radiation:
• Emitted by matter as a result of vibrational and rotational
movements of molecules, atoms and electrons.
• The energy is transported by electromagnetic waves (or
photons).
• Radiation requires no medium for its propagation,
therefore, can take place also in vacuum.
• All matters emit radiation as long as they have a finite
(greater than absolute zero) temperature

4. Thermal radiation:
• Absorptivity, α, the fraction of
incident radiation absorbed.
• Reflectivity, ρ, the fraction of
incident radiation reflected.
• Transmissivity, τ, the fraction of
incident radiation transmitted
Reflected
Radiation
Absorbed
Radiation
Transmitted
Radiation
1=++
++=
Q
Q
Q
Q
Q
Q
QQQQ


From Conservation of Energy, that:
Hence:
α + ρ + τ = 1
Body with α ＝1, — Absolute black-body
Body with ρ ＝1，— Absolute white-body
Body with τ ＝1，—Absolute transparent
body.

5. Black Body radiation
Black body (definition): A hypothetical object that
absorbs all of the radiation that strikes on it. It
also emits radiation (“Energy flux”) at a
maximum rate for its given temperature. For an
ideal black body ,
α ＝1
The Sun is very similar to an
“ideal emitter” (or “Black body”)
(NOTE: the Earth isn’t as ideal as a “black body”

6. Black Body radiation

7. Thermal Radiation
The thermal radiation have two important features:
❖Continuous frequency spectrum that depends only on the body's
temperature
❖Radiation is emitted by all parts of a plane surface in all direction
into the hemisphere above the surface, but the directional
distribution of emitted (incident) radiation is not uniform

8. Radiation Intensity
• Due to the directional distribution feature of thermal
radiation, we need a quantity to describes the magnitude of
radiation emitted or incident in specified direction.
• This quantity is radiation intensity denoted by I. It is the
rate of energy emitted ‘dq’ at wavelength λ at θ and Ф
direction per unit area of emitting surface normal to this
direction per unit solid angle d𝝎 about this direction per
unit wavelength interval dλ
𝑰 λ, θ, Ф =
𝒅𝒒
𝒅𝑨 𝟏 𝒄𝒐𝒔𝜽 ∙ 𝒅𝝎 ∙ 𝒅𝝀

9. Radiation Intensity
dA1 dA1·cos θ
θ
𝒅ω is a solid angle:
𝒅𝝎 =
𝒅𝑨 𝒏
𝒓 𝟐

10. Relation of Intensity to Emissive power
The radiation emitted by blackbody surface is isotropic (intensity Ib
is independent of the direction). Integrating the radiation power
for solid angles covering the whole upper hemisphere results to
relationship between the emissive power Eb and the intensity Ib.
𝑬 𝝀 is the spectral heat flux.
𝑬 𝝀 = න
𝟎
𝟐𝝅
න
𝟎
ൗ𝝅
𝟐
𝑰 𝝀,𝒆 𝝀, 𝜽, 𝝓 𝒄𝒐𝒔𝜽𝒔𝒊𝒏𝜽𝒅𝜽 𝒅𝝓 = π𝐼 𝑏

11. • Planck's law describes the
spectral density of
electromagnetic radiation
emitted by a black body in
thermal equilibrium at a given
temperature T.
• The Planck distribution is shown
in the figure as a function of
wavelength for different body
temperatures.
Planck’s law
Black Body radiation

12. Plank’s Law
• The Planck law describes
theoretical spectral
distribution for the emissive
power of a black body.
• 𝐸𝜆,𝑏 =
𝐶1
𝜆5[exp
𝐶2
𝜆𝑇
−1]
• where C1=3.742x108
(W.mm4/m2) and
C2=1.439x104 (m m.K) are
two constants.
• 𝑰 𝝀,𝒃 𝝀, 𝑻 =
𝟐𝒉𝒄 𝒐
𝟐
𝝀 𝟓[𝒆𝒙𝒑
𝒉𝒄 𝒐
𝝀𝒌 𝑩 𝑻
−𝟏]
• Where ℎ = 6.626 × 10−34
𝐽 ∙ 𝑠 and
𝑘 𝐵 = 1.381 × 10−23
𝐽/𝐾 are the
universal Plank and
Boltzmann constants,
respectively.
• 𝑐 𝑜 = 2.998 × 108 𝑚/𝑠 is the speed
of light in vacuum, and T is
the absolute temperature of
the blackbody(K).

13. Wien’s Displacement Law
The blackbody spectral distribution has a maximum and
that the corresponding wavelength 𝝀 𝒎𝒂𝒙depends on
temperature. Peak can be found for different temps using
Wien’s Displacement Law:
𝝀 𝒎𝒂𝒙 𝑻 = 𝑪 𝟑
Where the third radiation constants
𝑪 𝟑 = 𝟐𝟖𝟗𝟖𝝁𝒎 ∙ 𝑲
Black Body radiation

14. Black Body radiation
If spectral intensity is no related to 𝝓, then
0≤θ≤π/2
0≤ϕ≤2π
ϕ
dϕ
θ
dθ dAn
dA1
r
n
I(θ)
Lambert’s Law
𝐼 𝜃 = 𝐼0 𝑐𝑜𝑠𝜃

15. Black Body radiation
If spectral intensity is no related to 𝝓, then
Lambert’s Law
𝐼 𝜃 = 𝐼0 𝑐𝑜𝑠𝜃
s
r

n

Our skin absorbs more photons
at noon than at evening even if
the intensity of radiation is the
same (neglecting photon
absorption in atmosphere).

16. Black Body radiation
The Stefan- Boltzmann law
The total, hemispherical emissive power, E(W/m2), is the rate at
which radiation is emitted per unit area at all possible wavelengths
and in all possible directions.
𝑬 = න
𝟎
∞
𝑬 𝝀 𝝀 𝒅𝝀
𝑬 = න
𝟎
∞
න
𝟎
𝟐𝝅
න
𝟎
ൗ𝝅
𝟐
𝑰 𝝀,𝒆 𝝀, 𝜽, 𝝓 𝒄𝒐𝒔𝜽𝒔𝒊𝒏𝜽𝒅𝜽𝒅𝝓 𝒅𝝀
For a blackbody, Substituting the Planck distribution into above
Equation, the total emissive power of a blackbody Eb may be
expressed in another way:

17. Black Body radiation
The Stefan- Boltzmann law
The total intensity associated with blackbody emission is 𝑰 𝒃 =
𝑬 𝒃
𝝅
𝑬 𝒃 = න
𝟎
∞
𝑪 𝟏
𝝀 𝟓[𝒆𝒙𝒑
𝑪 𝟐
𝝀𝑻
− 𝟏]
𝒅𝝀 Performing the integration, it may be shown that
𝐸 𝑏 = 𝜎𝑇4 The result is termed the Stefan–Boltzmann law. It
can be stated as “The emissive power of a black body
(per unit area per unit time) is directly proportional
to the fourth power of its absolute temperature”.
Where the unit is ：
W/m2. （ b means
black body）
𝜎 is Proportionality constant called Stefan-Boltzmann constant.
𝜎= 5.676 x 10-8 W/m2-K4 unit is：W/m2K4

18. What we know about blackbody radiation
• the shape of the distribution
• the peak shifts according to Wien's law
• the total power output is described by the Stefan-
Boltzmann law

19. Practical body
Practical body has smaller emissive power than that of black body in the
same temperature. The ratio of the emissive power of the practical body to
the black body is called emissivity, i.e.



bE
E
=)(
4
TE =
So, for any practical body, we have：
A blackbody is said to be a diffuse
emitter since it emits radiation energy
uniformly in all directions.

20. Practical body
Kirchhoff’s law:
Imagine two parallel plates, one, which is a blackbody surface
(b=1) and the other one is gray (α,).
Eb(𝑇1)
Eb(𝑇2)
(1- α)Eb(𝑇2)
reflected
radiation
radiation
emitted by
gray plate
received
radiation
Resulting flux from left to right
Eb(𝑇1)- (1- α)Eb(𝑇2)-Eb(𝑇2)=0

21. Practical body
For thermal balance， 𝑇1 = 𝑇1 =T
Then ,
Eb
α
=
Eb

The Kirchhoff's law :“The emissivity of a body radiating energy at a temperature,
T, is equal to the absorptivity of the body when receiving energy from a source at
a temperature, T.”
Emissivity equals absorptivity. = α (ideal emitter of radiation is an ideal absorber).
Or, the higher absorptivity，has strong the emissivity.
In reality, (,,T) ≠  (,,T)

22. The radiation and View factor
Suppose we have two surfaces at temperature T1
and T2, but both are finite in area, and neither
surface is completely enclosed by the other.
An example might be the floor and ceiling of a
room. Only a fraction of the energy leaving the
ceiling strikes the floor and vice versa.
To account for this incomplete exchange of energy,
we define the view factor, F1-2.
F1-2 = Fraction of energy leaving A1 reaching A2.
In the same way , we can estimate F2-1
𝑇2
𝑇1
F1-2
F2-1

23. The radiation and View factor
Net radiation between the surfaces is：
𝑄12 = 𝐸 𝑏1 𝐴1 𝐹12 − 𝐸 𝑏2 𝐴2 𝐹21
Under the balance conditions, 𝑇1 = 𝑇2 𝑄12=0 , Eb1=Eb2
Then,
Hence，per unit time the radiation energy emitted by the first surface that
reaches second surface is: Eb1A1F1-2
Similarly, the energy from surface 2 that reaches surface 1 is：Eb2A2F2-1
From this equation, it can be found that the
geometric factor has no relation to the process.
𝐴1 𝐹12 = 𝐴2 𝐹21

24. The radiation and View factor
With the relationship of 𝐴1 𝐹12 = 𝐴2 𝐹21, we can calculate the radiation of two black
surfaces:
𝑄12 = (𝐸 𝑏1−𝐸 𝑏2)𝐴1 𝐹12 = (𝐸 𝑏2−𝐸 𝑏1)𝐴2 𝐹21
𝑄12 =
(𝐸 𝑏1−𝐸 𝑏2)
1
𝐴1 𝐹12
=
𝜎𝑇1
4
−𝜎𝑇2
4
𝑅 𝑟
=
(𝐸 𝑏1−𝐸 𝑏2)
𝑅 𝑟
Where, 𝑅 𝑟 is called radiation resistance for heat transfer between two surfaces.
1/(A1F12)
𝐸 𝑏1 𝐸 𝑏2
𝑅 𝑟 =
1
A1F12

25. View factor
✓ Very important coefficient to evaluate the radiation.
Properties
1. Enclosures:
Also called completeness of the geometric factor
In order that we might apply conservation of energy to
the radiation process, we must account for all energy
leaving a surface. We imagine that the surrounding
surfaces act as an enclosure about the heat source which
receive all emitted energy. For an N surfaced enclosure,
we can then see that:
1
1
, ==
N
j
jiF

26. View factor
✓ Very important coefficient to evaluate the radiation.
Properties
2. Reciprocity Relation:
1 2
Ai Fij = Aj Fji
𝑖. 𝑒.
𝐴1 𝐹12 = 𝐴2 𝐹21
The reciprocity theorem allow one to
calculate Fij if one already know Fji using
the areas of two surfaces.

27. View factor
✓ Very important coefficient to evaluate the radiation.
Properties
3. Associative Rule
i
j
k
𝐹𝑖−(𝑗+𝑘) = 𝐹𝑖−𝑗 + 𝐹𝑖−𝑘
And also,
𝐴𝑗+𝑘 𝐹 𝑗+𝑘 −𝑖 = 𝐴𝑗 𝐹𝑗−𝑖 + 𝐴 𝑘 𝐹𝑘−𝑖
The fraction of energy leaving surface i and
striking the combined surface j+k will equal the
fraction of energy emitted from i and striking j
plus the fraction leaving surface i and striking k.

28. View factor
✓ Very important coefficient to evaluate the radiation.
Properties
4. The geometric factor of two infinite plates.
𝐹12 = 𝐹21 = 1
X12 X21
𝐹12𝐹21
Since, the both plates are facing each
other parallelly,

29. View factor
✓ Very important coefficient to evaluate the radiation.
Properties
5. Curved surfaces.
𝐹2,1 =
𝐴1
𝐴2
A non-concave surface is completely
enclosed by other surface, the radiation
from 1 to 2 is received completely by 2，
So，F1，2＝1，at the same time，
F1
F2
A1
A2

30. View factor
✓ Very important coefficient to evaluate the radiation.
Properties
Three-Dimensional Geometry: Example
( )
1 222
2
2
1 4
2
1
1
/
/
/ /
ij j i
j
i
i i j j
F S S r r
R
S
R
R r L R r L
  = − −   
+
= +
= =
Coaxial Parallel Disks

31. Grey Body Radiation
The absorptivity of a grey body is lesser than 1.
So, some radiation striking on a grey body will be reflected back.
Radiosity, J , the total radiant energy leaving a body per unit area per unit
time.
Irradiation, G , the total radiant energy incident on a body per unit area per
unit time.
(−)
1 2
E1
E1

32. Grey Body Radiation
(−)
1 2
E1
E1
Net heat transfer from body：
AGJQ )( −=
The net emissive energy is
GEGEJ b )1(  −+=+=
Eliminate G，and note ：= α ，then：
A
JEAJE
Q bb
 /)1(
)(
/)1(
)(
−
−
=
−
−
=

33. Grey Body Radiation
b J1
(−)F1ൗ
(1 − 1)
1 𝐴111
1
11
1
1
A
JE
Q b

−
−
=
Electrical Analogy
Where, ൗ(1−1)
1 𝐴1
, is called surface thermal resistance
Grey body has a radiation resistance on its surface.
Therefore, its emissive power will decrease.

34. Grey Body Radiation
Hence，for any two grey surfaces, the radiation heat transfer can be expressed as：
𝑄12 =
(𝐸 𝑏1−𝐸 𝑏2)
1
𝐴1 𝐹12
+
1−1
1 𝐴1
+
1−2
2 𝐴2
Eb1 Eb2
J1 J2
1 − 1
1 𝐴1
1
𝐴1 𝐹12
1 − 2
2 𝐴2
Where,
1
𝐴1 𝐹12
is Space radiation resistance
1−1
1 𝐴1
&
1−2
2 𝐴2
is Surface resistances.

35. Grey Body Radiation
Electrical Analogy
Two infinite parallel plates
1 2
X1,2=1 X2,1=1F2-1 =1
F1-2 =1𝐴1
𝐴2
1 F1-2 = F2-1 =1
𝑄12 =
𝜎(𝑇1
4
− 𝑇2
4
)𝐴1
1
1
+
1
2
− 1

36. Grey Body Radiation
Electrical Analogy
A small body in a big space
𝐴1
𝐴2
0 F1-2 =1
A1
A2
𝑄12 = 𝜎1(𝑇1
4
− 𝑇2
4
)𝐴1

37. Grey Body Radiation
Insulation Sheet
Eb1 J1
1/A3X3,2
Q1
A3,ε3,T3
J31 Eb3 J32 J
1 3 2
1-ε1/ε1A1 1/A1X1,3 1-ε31/ε31A3 1-ε32/ε32A3
Before inserting a sheet, the radiation resistance between
two surfaces only includes two surface resistances and
one geometric resistance. After inserting the sheet, the
resistance will increase two surface resistances and one
geometric resistance. Hence, the total resistance will
increase and the heat transfer will decrease.
𝑄12 = 𝜎(𝑇1
4
− 𝑇2
4
)𝐴1 1=2 =Before Insulation If

38. Grey Body Radiation
Insulation Sheet
Before inserting Sheet
Q1
Eb1 J1 J2 Eb2
Q2
1-ε1/ε1A1 1/A1X1,2 1-ε2/ε2A2
A1
ε1
T1 T2
ε2
A2
Eb1 Eb2
J1 J2
1 − 1
1 𝐴1
1
𝐴1 𝐹12
1 − 2
2 𝐴2
Have
• Two surface resistances
• One geometric resistance
𝑄12 = 𝜎(𝑇1
4
− 𝑇2
4
)𝐴1
1=2 =If
F1-2 = F2-1 =1

39. Grey Body Radiation
Insulation Sheet
After inserting Sheet
Eb1 J1
Q2
1/A3X3,2
Q1
A3,ε3,T3
J31 Eb3 J32 J2 Eb2
1 3 2
1-ε1/ε1A1 1/A1X1,3 1-ε31/ε31A3 1-ε32/ε32A3 1-ε2/ε2A2
1
𝐴3 𝐹32
1
𝐴1 𝐹13
1 − 31
31 𝐴3
1 − 32
32 𝐴3
1 − 2
2 𝐴2
1 − 1
1 𝐴1
Have
• Four surface resistances
• Two geometric resistance
Hence, the effective heat
flow rate decreases and
acts as insulation.

40. Grey Body Radiation
Insulation Sheet
For infinite parallel plates, the geometric factor is
𝐹13 = 𝐹31 = 𝐹12 = 1
AAAA === 321
1
11
)(
21
1
4
2
4
1
2,1
−+
−
=

 ATT
Q b
Before inserting the
sheet, heat transfer
is:
After inserting the
sheet, heat transfer is:
1
11
1
11
)(
232311
4
2
4
1
2,33,12,3,1
−++−+
−
===

 ATT
QQQ b
Obviously
2,12,3,1 QQ   ==== 232311If
2,12,3,1
2
1
QQ =
Hence,

41. Grey Body Radiation
Insulation Sheet
 ==== 232311If
2,12,3,1
2
1
QQ =Hence,
With the same way, inserting n sheets between two infinite parallel plates
with same emissivity, the heat transfer is,
2,12,,1
1
1
Q
n
Q n
+
=
Hence, to increase insulation effect, the low emissivity sheet should be used.
shoeldwithoutshieldswith A
q
nA
q






+
=






1
1

42. Heat transfer coefficient for radiation
✓ A heat transfer coefficient for radiation is sometimes defined analogously to
the convection coefficient.
✓ 𝛼 𝑟 is defined as a radiation coefficient.
✓ We know,
TT R
TTTT
R
TT
Q
))(()(
2
2
2
1
2
2
2
1
4
2
4
1
2,1
−+
=
−
=

)(
))(()(
21
21
2
2
2
1
4
2
4
1
2,1 TT
R
TTTT
R
TT
Q
TT
−
++
=
−
=

Finally, radiation coefficient
T
r
AR
TTTT ))(( 21
2
2
2
1 ++
=


)( 212,1 TTAQ r −= Hence

43. Heat transfer coefficient for radiation
On the other hand, we know
Then the radiation coefficient is
Again, we have:
)( 2112,1 TTAQ r −= 
))()(()( 2121
2
2
2
1121
4
2
4
11212,1 TTTTTTAXTTAXQ −++=−= −− 𝐹12 𝐹12
))(( 21
2
2
2
121 TTTTXr ++= −  𝐹12

44. Thank you for your
time。。。
谢谢你们