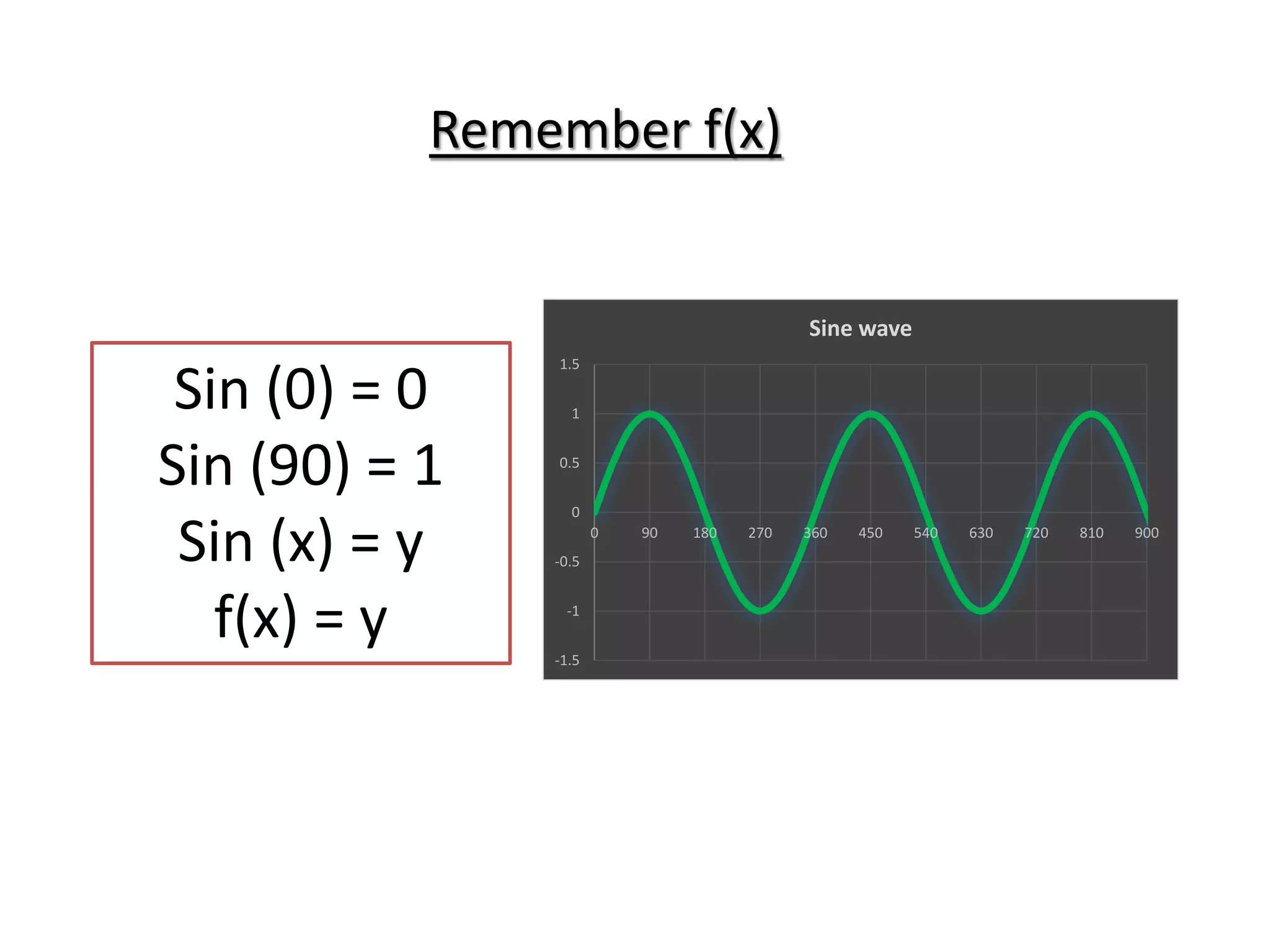
The document summarizes the time-independent Schrodinger wave equation, which describes standing waves as a function and can be written as: ∇2ψ + 8π2m/h2(E - V)ψ = 0 Where ψ is the wave function, ∇2 is the Laplacian operator, m is mass, h is Planck's constant, E is the total energy, and V is the potential energy. This equation describes standing waves in three dimensions using coordinates x, y, and z.

1. Time independent Schrodinger
wave equation
Dr. Mithil Fal Desai
Shree Mallikarjun and Shri Chetan Manju Desai
College Canacona Goa
Ĥ𝚿 = 𝑬𝚿

2. 𝛙 = wave function
𝐦 = mass
h = plank constant
E = total energy
V = potential energy
Schrodinger time independent wave equation
𝐝𝟐
𝛙
𝐝𝐱𝟐
+
𝐝𝟐
𝛙
𝐝𝐲𝟐
+
𝐝𝟐
𝛙
𝐝𝐳𝟐
+
𝟖𝛑𝟐
𝐦
𝐡𝟐
(𝐄 − 𝐕)𝛙 = 𝟎

3. Sin (0) = 0
Sin (90) = 1
Sin (x) = y
f(x) = y
Remember f(x)
-1.5
-1
-0.5
0
0.5
1
1.5
0 90 180 270 360 450 540 630 720 810 900
Sine wave

4. -1.5
-1
-0.5
0
0.5
1
1.5
0 90 180 270 360 450 540 630 720 810 900
sinx (dsinx/dx)=cosx d(cosx)/dx =-sinx
Understanding first and second derivative
Difficult?

5. Understanding first and second derivative
(easy way)
0
50
100
150
0 2 4 6
distance speed accelaration
Time
Distanc
e
speed acceleration
t x
dx/dt
=speed
d speed/dt=
acceleration
0 0 2 1
1 2 3 2
2 5 5 10
3 10 15 15
4 25 30 20
5 55 50 30
6 105 80 35
7 185 115
8 300

6. Schrodinger wave equation
𝒂𝒏𝒈𝒖𝒍𝒂𝒓 𝒘𝒂𝒗𝒆 𝒏𝒖𝒎𝒃𝒆𝒓
𝒌 =
𝟐𝝅
λ
𝐝𝟐𝒇(𝒙)
𝐝𝐱𝟐 = −
𝟒𝝅𝟐
λ𝟐 𝒇 𝒙 …….1
A standing wave having wavelength (λ) that has an amplitude at any point
along x direction is mathematically described as a function f(x)

7. 𝐝𝟐ψ
𝐝𝐱𝟐 = −
𝟒𝝅𝟐
λ𝟐 ψ
--2
If a wave function f(x) is represented as 𝝍 (psi) the
equation can be written as
Schrodinger wave equation

8. 𝐝𝟐𝛙
𝐝𝐱𝟐 +
𝐝𝟐𝛙
𝐝𝐲𝟐 +
𝐝𝟐𝛙
𝐝𝐳𝟐 = −
𝟒𝝅𝟐
λ𝟐 ψ
--3
When this standing wave is considered in 3 dimensions
having x, y and z coordinates
Schrodinger wave equation

9. 𝛁𝟐
𝛙 = −
𝟒𝝅𝟐
λ𝟐
ψ
--4
Schrodinger wave equation
If,
𝐝𝟐𝛙
𝐝𝐱𝟐
+
𝐝𝟐𝛙
𝐝𝐲𝟐
+
𝐝𝟐𝛙
𝐝𝐳𝟐
= 𝛁𝟐
𝛙
𝛁 is called Del Operator

10. λ =
𝒉
𝒎𝒗
𝜆2
=
ℎ2
𝑚2𝑣2
--5
Schrodinger wave equation
𝒗 𝒊𝒔 𝒗𝒆𝒍𝒐𝒄𝒊𝒕𝒚
de Broglie states that

11. 𝛁𝟐
𝝍 = −
𝟒𝝅𝟐
𝒉𝟐
𝒎𝟐𝒗𝟐
𝝍
𝜵𝝍 +
𝟒𝝅𝟐
𝒎𝟐
𝒗𝟐
𝒉𝟐
𝝍 = 𝟎
--6
Schrodinger wave equation
From equation 4 and 5

12. 𝑬 = 𝑲. 𝑬. + 𝑽
K. E.= 𝑬 − 𝑽
𝟏
𝟐
𝒎𝒗𝟐
= 𝑬 − 𝑽
𝒗𝟐
=
𝟐
𝒎
(𝑬 − 𝑽)
--7
Schrodinger wave equation
The total energy (E) of system is given as

13. 𝛁𝟐
𝝍 +
𝟒𝝅𝟐𝒎𝟐
𝒉𝟐
{
𝟐
𝒎
𝑬 − 𝑽 }𝝍 = 𝟎
𝛁𝟐
𝝍 +
𝟖𝝅𝟐
𝒎
𝒉𝟐
𝑬 − 𝑽 𝝍 = 𝟎
---8
Schrodinger wave equation
From equation 6 and 7
Time independent
Schrodinger wave equation

14. Schrodinger wave equation
general form
Ĥ= Hamiltonian operator,
E= Eigen value, specific values of energy
Ĥ𝚿 = 𝑬𝚿
Can you state Ĥ from equation 8?