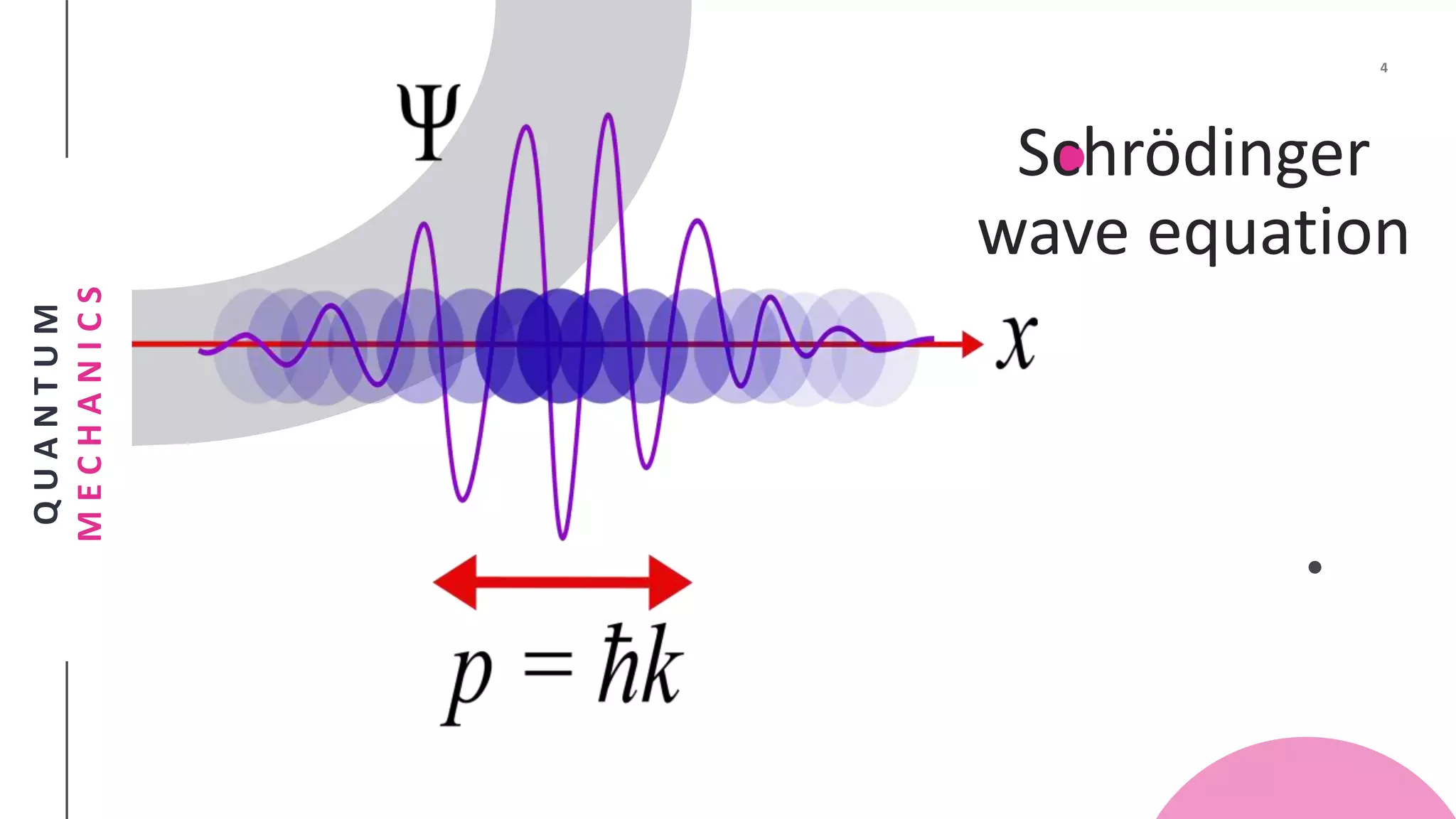
The document provides an overview of quantum mechanics concepts including: - Erwin Schrodinger developed the Schrodinger wave equation which describes the energy and position of electrons. - The time-dependent and time-independent Schrodinger equations are presented for 1D systems. Solutions include plane waves and wave packets. - The postulates of quantum mechanics are outlined including the use of wavefunctions and Hermitian operators to represent physical quantities. - Differences between the interpretations of quantum mechanics by Heisenberg and Schrodinger are briefly discussed.

1. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
M.M.H. COLLEGE GHAZIABAD
Session 2020-21
Department of chemistry
M.Sc. (CHEMISTRY), I SEMESTER

2. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
SNO.
Schrödinger wave equation
Postulates of quantum
mechanics
1. Who is Erwin Schrödinger? First and second postulate
2. The Schrödinger equation Third , fourth and fifth postulate
3. The Schrödinger equation in 1-D Sixth and seven postulates
4. The Schrödinger equation in 1-D: Wave packets
Thank you
5. The Schrödinger equation in 1-D: Stationary states
Bibliography
6. Heisenberg vs Schrödinger
7. Conclusion
INDEX

3. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
S c h r ö d i n g e r w a v e
e q u a t i o n
&
Po s t u l a t e s o f q u a n t u m m e c h a n i c s

4. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
Schrödinger
wave equation

5. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
Who is Erwin
Schrödinger?
was a Nobel Prize-winning Austrian-
Irish physicist who developed a number of
fundamental results in quantum theory:
the Schrödinger equation provides a way to
calculate the wave function of a system and how it
changes dynamically in time
In addition, he was the author of many works on
various aspects of physics: statistical
mechanics and thermodynamics, physics of
dielectrics, colour theory, electrodynamics, general
relativity, and cosmology, and he made several
attempts to construct a unified field theory. He is
also known for his "Schrödinger's cat" thought
experiment.

6. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
S c h r ö d i n g e r ' s
e q u a t i o n i n s c r i b e d
o n t h e g r a v e s t o n e o f
A n n e m a r i e a n d E r w i n
S c h r ö d i n g e r .
( N e w t o n ' s d o t
n o t a t i o n f o r t h e t i m e
d e r i v a t i v e i s u s e d . )

7. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
The Schrödinger equation
• Schrodinger wave equation is a mathematical expression
describing the energy and position of the electron in space and
time, taking into account the matter wave nature of the electron
inside an atom.
• It is based on three considerations. They are;
• Classical plane wave equation,
• Broglie’s Hypothesis of matter-wave, and
• Conservation of Energy.
• Schrodinger equation gives us a detailed account of the form of
the wave functions or probability waves that control the motion of
some smaller particles. The equation also describes how these
waves are influenced by external factors. Moreover, the equation
makes use of the energy conservation concept that offers details
about the behaviour of an electron that is attached to the nucleus.

8. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
• Besides, by calculating the Schrödinger equation we obtain Ψ and Ψ2, which
helps us determine the quantum numbers as well as the orientations and the
shape of orbitals where electrons are found in a molecule or an atom.
• There are two equations, which are time-dependent Schrödinger equation and
a time-independent Schrödinger equation.
• Time-dependent Schrödinger equation is represented as;
• Where,
• I = imaginary unit, Ψ = time-dependent wavefunction, h2 is h-bar, V(x) =
potential and
H^= Hamiltonian operator.
The Schrödinger equation

9. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S The Schrödinger equation in 1-D
We found that the one-dimensional Schrödinger
equation for a free particle of mass m is
How do we interpret the complex solution ? This
represents a distribution of “something” in space and time. Any real
quantity, however, must have a real solution. Recall that we interpreted
the interference intensity pattern as representing the square of the
electric field, and individual photons land on a screen with a probability
given by the intensity pattern (more land where the intensity is high,
fewer land where it is low). Likewise, the quantity
is the (real) probability in space and time where the particle will be
found, where the * represents the complex-conjugate found by replacing
I with -I.
The square of the abs. value of the wave function, |(x, t)|2, is the
probability distribution function. It tells us the probability of finding the
particle near position x at time t.
−
ℏ2
2𝑚
𝜕2
Ψ 𝑥, 𝑡
𝜕𝑥2
= 𝑖ℏ
𝜕Ψ 𝑥, 𝑡
𝜕𝑡
Ψ(𝑥, 𝑡) = 𝐴𝑒𝑖 𝑘𝑥−𝜔𝑡
Ψ(𝑥, 𝑡) 2
= Ψ(𝑥, 𝑡)Ψ∗
(𝑥, 𝑡) = 𝐴𝑒𝑖 𝑘𝑥−𝜔𝑡
𝐴∗
𝑒−𝑖 𝑘𝑥−𝜔𝑡

10. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S The Schrödinger
equation in 1-D: Wave
packets
If is a solution to the Schrödinger equation,
any superposition of such waves is also a solution. This would be
written:
A free-particle wave packet localized in space (see Figure 40.6 at
right) is a superposition of states of definite momentum and energy.
The function itself is “wavy,” but the probability distribution function
is not.
The more localized in space a wave packet is, the greater the range of
momenta and energies it must include, in accordance with the
Heisenberg uncertainty principle
The Schrödinger equation discussed so far is only for a free particle
(in a region where potential energy U(x) = 0). We will now add non-
zero U(x).
Ψ 𝑥, 𝑡 = 𝐴𝑒𝑖 𝑘𝑥−𝜔𝑡
Ψ(𝑥, 𝑡) =
−∞
∞
𝐴(𝑘)𝑒𝑖 𝑘𝑥−𝜔𝑡
𝑑𝑘

11. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
The Schrödinger equation in 1-D: Stationary states
If a particle of mass m moves in the presence of a potential energy function
U(x), the one-dimensional Schrödinger equation for the particle is
This equation can be thought of as an expression of conservation of energy, K +
U = E. Inserting ,the first term is K times .
Likewise, the term on the RHS is E times .
For a particle in a region of space with non-zero U(x), we have to add the term
U(x)(x, t) on the left to include the potential energy.
Let’s write the wave function in separable form, where the lower-case y(x) is
the time-independent wave function.
Further, we can write , so that
 
   
 
2
2
2
, ,
, (general 1D Schrodinger equation)
2
x t x t
U x x t i
m x t
  
-   
 
 
( , )
i kx t
x t Ae

-
  ( , )
x t

 
     
2
2 2 2 2 2
2
2
,
( ) , , ,
2 2 2 2
x t k p
ik x t x t x t
m x m m m
 
-  -     

( , )
x t

 
   
,
( ) , ,
x t
i i i x t x t
t
 

 -   

( , ) ( )
ikx i t i t
x t Ae e x e
 
y
- -
  
/
E
  /
( , ) ( ) iEt
x t x e
y -
 

12. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
The Schrödinger equation in 1-D: Stationary states
For such a stationary state the probability distribution function |(x, t)|2 =
|y(x)|2 does not depend on time, which you can see by
In this case, the time-independent one-dimensional Schrödinger equation for a
stationary state of energy E simplifies to
where the time derivative has been explicitly taken on the RHS
We will spend most of the rest of the lecture on solving this equation to find the
stationary states and their energies for various situations.
Note: The term stationary state does not refer to the motion of the particle it
represents. The particles are not stationary, but rather their probability
distribution function is stationary (does not depend on time), rather like a
standing wave on a string.
         
2 2
* / * /
, , , ( )
iEt iEt
x t x t x t x e x e x
y y y
-
     
 
     
2
2
2
(time-independent 1D Schrodinger equation)
2
d x
U x x E x
m dx
y
y y
-  

13. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
HEISENBERG VS
Heisenberg’s picture was basically statistical. According to
them the behaviour of the world’s particles can not be
described classically but only probabilistically. For them
asking questions such as “where is the particle in between
measurements” was simply meaningless, we can only talk
about measurements, and we can only make probabilistic
predictions for the outcome of those measurements. For
them the famous wave-particle duality was a consequence of
this intrinsic probabilistic nature of particles, but they never
really considered matter particles as being real waves or as
SCHRÖDINGER
Schrödinger as is well known developed his famous wave
equation, which extended the original De-Broglie’s concept
of real matter waves and achieved a wave formulation which
he proved to be totally equivalent to the statistical
formulation of Born and Heisenberg. Schrödinger himself
was never too determined about the physical meaning of his
wave, but mostly he believed that the mass and charge of
the electron was indeed delocalized in between
measurements, it was smeared out across the region of
space described by the wave.

14. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
CONCLUSION
In conclusion, the Schrodinger equation has been derived to be the (local)
condition the wavefunction must satisfy at each point in order to fulfil the total
(global) energy equation. In an analogous fashion, we can derive the three
dimensional, time-dependent Schrodinger equation and also the other
wavefunction equations from the respective total energy equations

15. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
Postulates of
quantum
mechanics

16. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
First postulate: The physical
state of a system at time t is described by the
wave function
The postulates of quantum mechanics for the
mechanical treatment of the structure of atom rest
upon a few postulates which, for a system moving in
one dimension, say the - coordinate, are given
below.
( , )
x t

Second postulate: The wave
function Ψ(r,t) depends upon position
coordinate r i.e., Ψ(r) and also on time
coordinate t i.e., Ψ(t) and can be written as
Ψ(r.t) = Ψ(r). Ψ(t)
Also

17. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
T h i r d p o s t u l a t e :
A physically observable quantity can be
represented by a Hermitian operator. An
operator is said to be Hermitian operator, if it
satisfies the following

18. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S

19. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
“If you think you
understand
quantum mechanics,
then you don’t.”
By
Richard feynman

20. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
T H A N K YO U
SUBMITTED TO :
Mrs. ANURADHA SINGH
Dr. RATNA SHERRY
SUBMITTED BY :
VIDHI WALIA

21. Q
U
A
N
T
U
M
M
E
C
H
A
N
I
C
S
• [1] Griffiths, D., Introduction to Quantum Mechanics, 2nd ed.,
Prentice-Hall, New Jersey, 2004.
• [2] Greiner, W., Quantum Mechanics an Introduction, Springer, New
York, 1994.
• [3] Principle of Physical chemistry by B.K. Puri
Bibliography