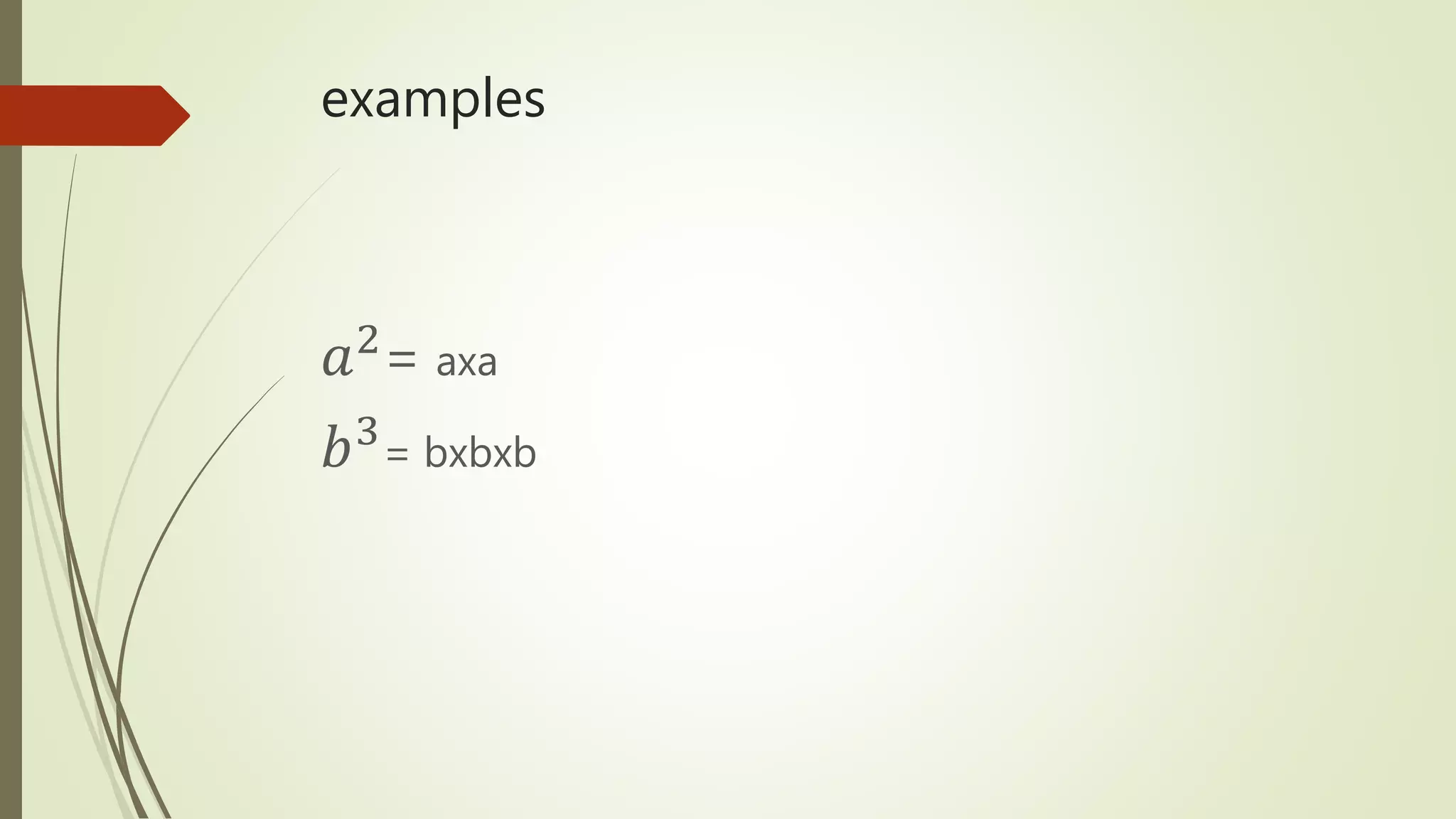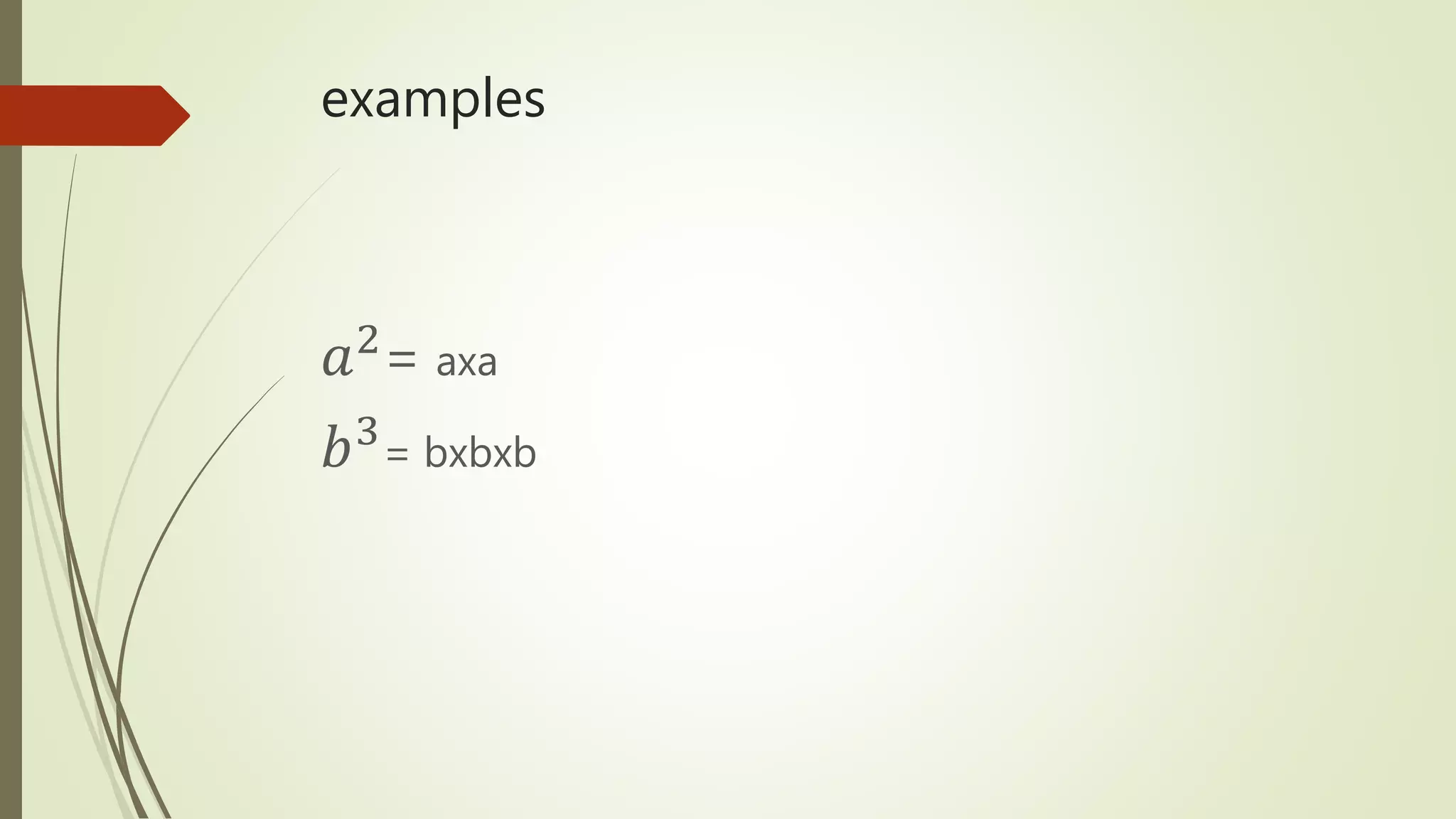
This document discusses the laws of exponents and operations involving exponents. It explains that an exponent shows the factor of a number and provides examples. It also outlines the following laws of exponents: (1) When multiplying terms with the same base, add the exponents. (2) When dividing terms with the same base, subtract the exponents. (3) When raising a power to a power, multiply the exponents. (4) When raising a product to a power, raise each factor to that power. (5) Any number or variable raised to the power of 0 is equal to 1.

1. The laws of exponents
Operations on exponents
By singwane NP, 201436252

2. Required to know the following:
 Operations which includes multiplying, addition,
subtraction as well as division.
 How to solve fractions.

3. The learning process will include the ff:
 What is an exponent
 How to perform operations using the laws of
exponents.

4. exponent
 It shows the factor of a number
𝑥 𝑚
Where x is the base and m is the exponent

5. examples
𝑎2
= axa
𝑏3
= bxbxb

6. Addition and subtraction
You can only add and subtract exponents which have
the same like terms.
𝑦2
+ 𝑦2
+𝑦3
= 2 𝑦2
+ 𝑦3

7. Laws of exponents
 Multiplying
𝑎 𝑚
. 𝑎 𝑛
=𝑎 𝑚+𝑛
When multiplying we add the exponents if the bases are
the same.
𝑦2
.𝑦3
=𝑦2+3
=𝑦5

8. Division of exponents
𝑎 𝑚
𝑎 𝑛 = 𝑎 𝑚−𝑛
When dividing, we subtract the exponents if and only if
the bases are the same.
𝑦4
𝑦2 =𝑦4−2
=𝑦2

9. Power to power
( 𝑎 𝑚
) 𝑛
=𝑎 𝑚.𝑛
when you raise a power to a power, you have to
multiply the exponents.
(𝑥2
)3
=𝑥2.3
=𝑥6

10. Power to product
(𝑎𝑏) 𝑚=𝑎 𝑚.𝑏 𝑚
When you raise a product ta a power, you have to raise
each factor to the power.
(2𝑥𝑦)3
=23
.𝑥3
.𝑦3
= 8.𝑥3
.𝑦3

11. 0 as an exponent
Any number or variable raised to the power 0 is equals
1
𝑥0
=1
𝑦0
=1
20
=1

12. Refferences
https://www.youtube.com/watch?v=A1wKTiBTsfk