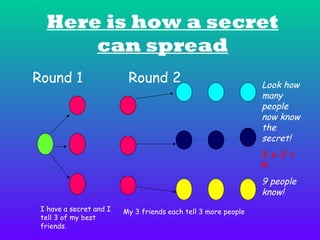
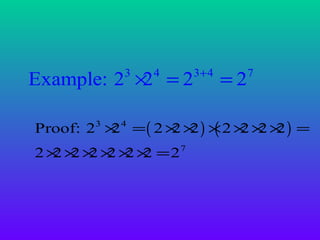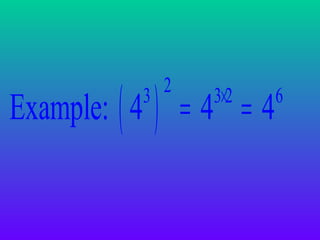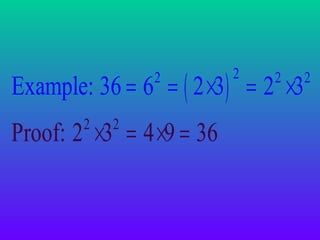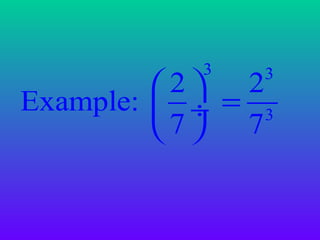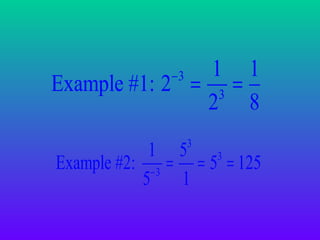Exponents are used to represent repeated multiplication of a number, called the base. The exponent indicates how many times the base is multiplied. Some key laws for exponents include: when multiplying the same bases, add the exponents; when dividing the same bases, subtract the exponents; when raising a power to another power, multiply the exponents. Exponents provide a shorthand way to write very large or small numbers.

2. What is an exponent?
Exponents are a
shorthand way to show
a larger number.

3. Where is an exponent
located at?
Exponents are sometimes
referred to as “powers.”
Base
6
4
Exponent

4. How do you read an
exponent?
A number with an exponent
is said to be "raised to the
power" of that exponent.
Let’s look at some
examples. . . .

5. 32 = three raised to the second
power or three squared
53 = five raised to the third
power or five cubed
74 = seven raised to the fourth
power

6. What does an
exponent mean?
We will use an example of
how the secret spread fast
to explain what does an
exponent mean.

7. How does a secret
spread so fast?
• The person with a secret tells a
friend.
• The friend promises never to tell
anyone.
• That same friend breaks the
promise and tells two more
friends.
• The two new friends tell two new
friends.

8. • The two new friends decide to
tell two more friends.
• This pattern occurs over and
over until many people have
been told.
• By the end of the day it is no
longer a secret!

9. Here is how a secret
can spread
Round 1
Round 2
Look how
many
people
now know
the
secret!
3 x 3 =
9
9 people
know!
I have a secret and I
tell 3 of my best
friends.
My 3 friends each tell 3 more people.

10. In an exponential expression, the base is the factor,
and the exponent tells the amount of times to
multiple that number by itself. (That is a mouthful!)
Your BASE = 3
3
4
Your EXPONENT = 4
• A base is a number that can be
expressed using an exponent.
• An exponent is the small number and is
referred to as a “power.”
3 means 3 x 3 x 3 or 27
4

11. LAWS OF
EXPONENTS

12. • Recall: A number in exponential form
has a base and an exponent. The
exponent indicates how many times
the base is used as a factor.
• In its exponential form:
a is the BASE and
b is the EXPONENT.
ab

13. NOTES
The laws of exponents show how to
SIMPLIFY
expressions in exponential form.

14. NOTES
In the next few slides, a and b are real
numbers and m and n are integers.

15. Product of powers
• To multiply powers with the same
base, add the exponents.
a ∙a = a
m
n
m+n

16. Example: 2 × = 2
2
3
4
3+ 4
=2
7
Proof: 23 × 4 = ( 2 × × ) × 2 × × × ) =
2
2 2 ( 2 2 2
2 × × × × × × =2
2 2 2 2 2 2
7

17. Power of a power
• To raise a number in exponential form
to a power, multiply the exponents.
(a ) = a
m n
m∙n

18. Example: ( 4 ) = 4 = 4
2
3
3×2
6

19. Power of a product
• To find a power of a product, find the
power of each factor and multiply.
(ab) = a b
m
m
m

20. Example: 36 = 6 = ( 2 ×3) = 2 ×3
2
Proof: 2 ×3 = 4 ×9 = 36
2
2
2
2
2

21. Power of zero
• Any nonzero number raised to the
power of zero is one.
a =1
0

22. Quotient of powers
• To find the quotient of powers with
the same base, subtract the
exponents.
a =a
n
a
m
m-n

23. •For example…
3 ÷3 =3
2
2
2-2
3 = 3 • 3 =9 =1
2
3 3•3
2
9
=3
0

24. Power of a quotient
To raise a quotient to a power, raise
both the numerator and denominator
to that power.
(a/b) = a /b
m
m
m

25. 3
3
2
2
Example:  ÷ = 3
7
7

26. Reciprocals
• To change a sign of an exponent, move
the expression to the denominator of
a fraction, or to the numerator.
a = 1/a
-n
n
1/a = a
-n
n

27. 1 1
Example #1: 2 = 3 =
2 8
−3
3
1 5 3
Example #2: − 3 = = 5 = 125
5
1

28. references
Maslijr, 2013, Laws of exponents, viewed 05 March 2014, from
http://www.slideshare.net/masljr/laws-of-exponents-23863798
Melnichenko, Y., 2008, Exponents, viewed 05 march 2014, from
http://www.slideshare.net/yelena585/exponents-presentation?qid=c977ae81-f7bd48bf-bf86-c88dd4657047&v=default&b=&from_search=30
Morris, B., 2012, Grade 6 exponents lesson, viewed 05 March 2014, from
http://www.slideshare.net/BobMorris72/math-exponents?qid=c977ae81-f7bd48bf-bf86-c88dd4657047&v=default&b=&from_search=2
Scallion, K., 2010, Rules of exponents, viewed 05 March 2014, from
http://www.slideshare.net/kscallion/rules-of-exponents
Wilkerosn,K., 2013, Exponents, viewed 05 march 2014, from
http://www.slideshare.net/katiewilkerosn/exponents-27460394?qid=c977ae81f7bd-48bf-bf86-c88dd4657047&v=default&b=&from_search=11

29. THE END