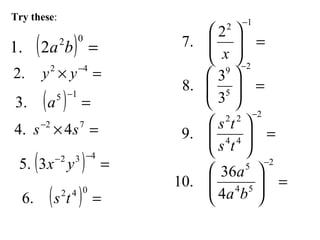Downloaded 117 times
More Related Content
Donna G. Bautista
- 1. Law of Exponents Donna G.Bautista BSEd 4-C
- 2. ExponentsExponents { 3 5Power base exponent 3 3 meansthat is the exponential form of t Example: he number 125 5 5 .125 = 53 means 3 factors of 5 or 5 x 5 x 5
- 3. The Laws ofExponents:The Laws of Exponents: #1: Exponential form: The exponent of a power indicates how many times the base multiplies itself. n n times x x x x x x x x − = × × ×××× × × ×144424443 3 Example: 5 5 5 5= × × n factors of x
- 4. #2: Multiplying Powers:If you are multiplying Powers with the same base, KEEP the BASE & ADD the EXPONENTS! m n m n x x x + × = So, I get it! When you multiply Powers, you add the exponents! 512 2222 93636 = ==× +
- 5. #3: Dividing Powers:When dividing Powers with the same base, KEEP the BASE & SUBTRACT the EXPONENTS! m m n m n n x x x x x − = ÷ = So, I get it! When you divide Powers, you subtract the exponents! 16 22 2 2 426 2 6 = == −
- 6. Try these: =× 22 33.1 =×42 55.2 =× 25 .3 aa =× 72 42.4 ss =−×− 32 )3()3(.5 =× 3742 .6 tsts =4 12 .7 s s =5 9 3 3 .8 =44 812 .9 ts ts =54 85 4 36 .10 ba ba
- 7. =× 22 33.1 =× 42 55.2 =×25 .3 aa =× 72 42.4 ss =−×− 32 )3()3(.5 =× 3742 .6 tsts 8133 422 ==+ 725 aa =+ 972 842 ss =×× + SOLUTIONS 642 55 =+ 243)3()3( 532 −=−=− + 793472 tsts =++
- 8.
- 9. #4: Power ofa Power: If you are raising a Power to an exponent, you multiply the exponents! ( ) nm mn x x= So, when I take a Power to a power, I multiply the exponents 52323 55)5( == ×
- 10. #5: Product Lawof Exponents: If the product of the bases is powered by the same exponent, then the result is a multiplication of individual factors of the product, each powered by the given exponent. ( ) n n n xy x y= × So, when I take a Power of a Product, I apply the exponent to all factors of the product. 222 )( baab =
- 11. #6: Quotient Lawof Exponents: If the quotient of the bases is powered by the same exponent, then the result is both numerator and denominator , each powered by the given exponent. n n n x x y y = ÷ So, when I take a Power of a Quotient, I apply the exponent to all parts of the quotient. 81 16 3 2 3 2 4 44 ==
- 12. Try these: ( )= 52 3.1 ( ) = 43 .2 a ( ) = 32 2.3 a ( ) = 2352 2.4 ba =− 22 )3(.5 a ( ) = 342 .6 ts = 5 .7 t s = 2 5 9 3 3 .8 = 2 4 8 .9 rt st = 2 54 85 4 36 .10 ba ba
- 13. ( ) = 52 3.1 () = 43 .2 a ( ) = 32 2.3 a ( ) = 2352 2.4 ba =− 22 )3(.5 a ( ) = 342 .6 ts SOLUTIONS 10 3 12 a 6323 82 aa =× 6106104232522 1622 bababa ==××× ( ) 4222 93 aa =×− × 1263432 tsts =××
- 14. = 5 .7 t s = 2 5 9 3 3 .8 = 2 4 8 .9 rt st = 2 54 85 4 36 10 ba ba SOLUTIONS ( ) 62232223 8199babaab == × 2 8224 r ts r st = ( ) 824 33 = 5 5 t s
- 15. #7: Negative Lawof Exponents: If the base is powered by the negative exponent, then the base becomes reciprocal with the positive exponent. 1m m x x − =So, when I have a Negative Exponent, I switch the base to its reciprocal with a Positive Exponent. Ha Ha! If the base with the negative exponent is in the denominator, it moves to the numerator to lose its negative sign! 93 3 1 125 1 5 1 5 2 2 3 3 == == − − and
- 16. #8: Zero Lawof Exponents: Any base powered by zero exponent equals one. 0 1x = 1)5( 1 15 0 0 0 = = = a and a and So zero factors of a base equals 1. That makes sense! Every power has a coefficient of 1.
- 17. Try these: ( )= 02 2.1 ba =× −42 .2 yy ( ) = −15 .3 a =×− 72 4.4 ss ( ) = −− 432 3.5 yx ( ) = 042 .6 ts = −12 2 .7 x = −2 5 9 3 3 .8 = −2 44 22 .9 ts ts = −2 54 5 4 36 .10 ba a
- 18. SOLUTIONS ( ) = 02 2.1ba =× −42 .2 yy ( ) = −15 .3 a =×− 72 4.4 ss ( ) = −− 432 3.5 yx ( ) = 042 .6 ts 1 2 2 1 y y =− 5 1 a 5 4s ( ) 12 8 1284 81 3 y x yx =−− 1
- 19. = −12 2 .7 x = −2 5 9 3 3 .8 = −2 44 22 .9 ts ts = −2 54 5 4 36 .10 ba a SOLUTIONS 4 4 1 x x = − ( ) 8 824 3 1 33== −− ( ) 44222 tsts = −−− 2 10 1022 81 9 a b ba =−−