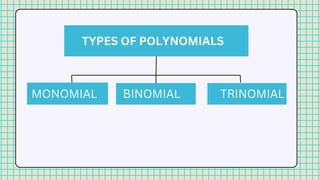
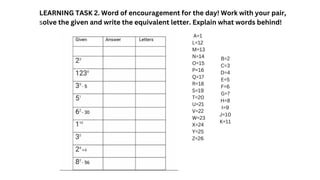
The document is a math lesson plan focusing on polynomials and laws of exponents, including definitions, objectives, and various mathematical rules. It includes interactive activities, such as card games and a relay race, for students to engage with the content. Additionally, it provides examples and matching exercises to reinforce understanding of exponential notation and operations.

1. Dear God,
May we, through your blessings,
† ADD purity to the world,
– SUBTRACT evil from our lives,
× MULTIPLY Your Good News, and
÷ DIVIDE Your gifts and share them with others.
Amen.
MATH PRAYER

3. what’s our previous
topic?

4. POLYNOMIALS
are the expressions in Maths, that includes
varibales, coefficients and exponents.

5. MONOMIAL BINOMIAL TRINOMIAL
TYPES OF POLYNOMIALS

6. I
CE
BREAKER
L
ET’S GO..
.

7. To play this game, the whole class will be divided unto 2 major groups
and the learners will decide who are their players for the game. In every
group have a pack of cards, and in the pack of cards we need twos,
threes, and five numbers and shuffle it. The first and second player will
choose two cards then each group will decide how to arrange their
cards by exponential form. When it’s done, calculate the answer. Higher
numbers will win the game!
MATH CARD GAMES

8. LEARNING TASK 2. Word of encouragement for the day! Work with your pair,
solve the given and write the equivalent letter. Explain what words behind!
A=1
L=12
M=13
N=14
O=15
P=16
Q=17
R=18
S=19
T=20
U=21
V=22
W=23
X=24
Y=25
Z=26
B=2
C=3
D=4
E=5
F=6
G=7
H=8
I=9
J=10
K=11

9. LAWS
LAWS
OF
OF
EXPONENTS
EXPONENTS

10. Objectives:
Define the exponential
notation, base, exponent and
the Laws of exponents
Derive inductively the laws of
exponents
Illustrate the Laws of
Exponents

11. Law of Exponents
Law of Exponents
one of a set of rules in algebra: exponents of
numbers are added when the numbers are
multiplied, subtracted when the numbers are
divided, and multiplied when raised by still
another exponent: am×aⁿ=am+n;
am÷aⁿ=am−n; (am)ⁿ=amn.

12. Product of Powers
y^3 * y^3= y^6
Examples:
2^3 * 2^4= 2^7 or 128
(xy)^a * (xy)^b = (xy)^(a+b)
To find the product of two numbers with
the same base, add the exponents.

13. Quotient of Powers
x^9/x^3= x^6
Examples:
3^5/3^3= 3^2 or 9
The quotient rule states that when exponents
with the same base are being divided, we simply
just subtract the exponents to simplify the
expression. (xy)^a / (xy)^b = (xy)^(a-b)

14. Power of a Power
(x^2)^3= x^6
Examples:
(5^2)^2= 5^4 or 625
If an expression of a base raised to a power is
being raised to another power, multiply the
exponents and keep the base the same.

15. Zero Exponent Rule
x^0= 1
Examples:
52^0= 1
States that any nonzero number raised to the
power of 0 is equal to 1. a^0=1

16. Negative Rule
a^-n =1/ a^n
Examples:
3^-2= 1/3^-2
1/3^2 or 1/9
The multiplicative inverses of the bases. The
negative exponent rule states that the base with
a negative exponent must be written as its
reciprocal.

17. 1.Product of Powers: (xy)^a * (xy)^b = (xy)^(a+b)
2.Quotient of Powers: (xy)^a / (xy)^b = (xy)^(a-b)
3.Power of a Power: (xy)^a)^b = (xy)^(ab)
4.Zero Exponent Rule. a^0=1 where a is not equal to
zero
5.Negative Rule. a^-n =1/ a^n
Law of Exponents
Law of Exponents

18. MATCHING TYPE: Determine the law of exponents by matching column A to column B.
Write the letter of your answer in the space provided before the number.
Column A
1 When multiplying two
exponential expressions
with the same base, you
add the exponents.
2 When dividing two
exponential expressions with
the same base, you subtract the
exponents.
3 When raising an exponential
expression to another exponent,
you multiply the exponents.
4 Any nonzero number raised
to the power of zero equals one.
5. A negative exponent on a base
is equivalent to the reciprocal of the
base raised to the positive exponent.
Column B
A. Zero Exponent
B. Power of a power
C. Quotient Rule
D. Product Rule
E. Negative Exponent Rule

19. 1. Z^3 Z^9
2. (7^3 )^4
3. X^6/ x^3
4. 103^0
5. 6^-2
Simplify fully:

20. EXPONENTS ACTION RELAY
DEVIDE THE CLASS INTO TEAMS. IN DOING THIS, THE TEACHER WILL
GIVE A PROBLEM INVOLVING LAWS OF EXPONENTS AND LEARNERS WILL
MAKE AN ACTIONS AND PASS IT TO THEIR MEMBERS. BASE EQUAL
SWAY, EXPONENTS EQUAL JUMP. WHEN THEY ARE DONE PASSING IT
THE LAST MEMBER OF THE GROUP GO IN FRONT SHOW THE ACTION
AND SOLVE THE PROBLEM. THE FIRST ONE WHO GET THE CORRECT
ANSWER WILL WIN!

21. Let’s Find Out: Appropriate Rule of Exponent to be Applied.
Identify and name the laws of exponent to be applied in simplifying in the given
exponential expressions below through solving.
1.(4x³) (4x)
2. (3a^2) ^3
3. (ab^2) ^3
4. a^-3
5. 839^0

22. THANK
THANK
YOUVERY
YOUVERY
MUCH!
MUCH!