Uploaded byPhil Saraspe
Laws Of Exponents
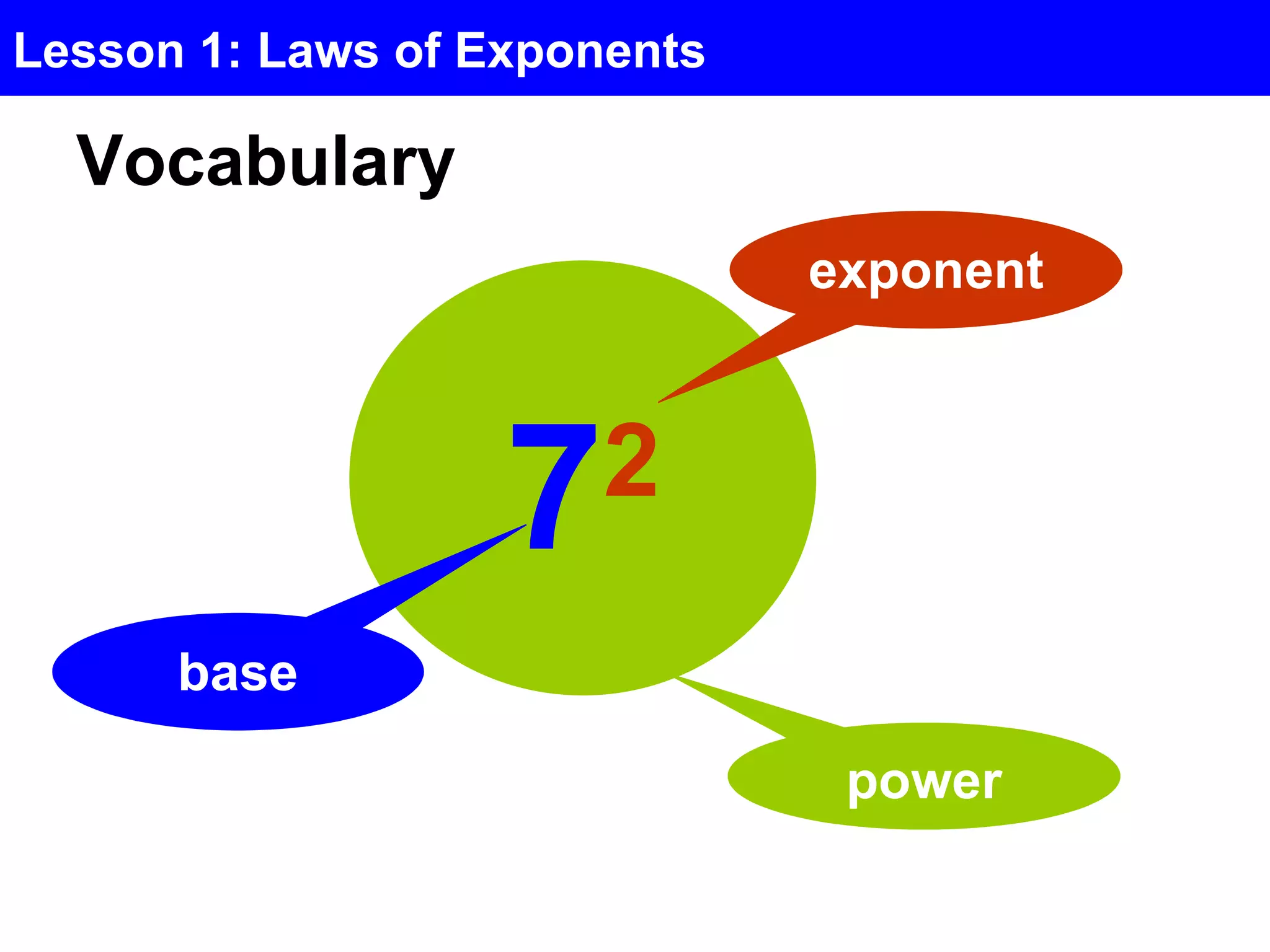
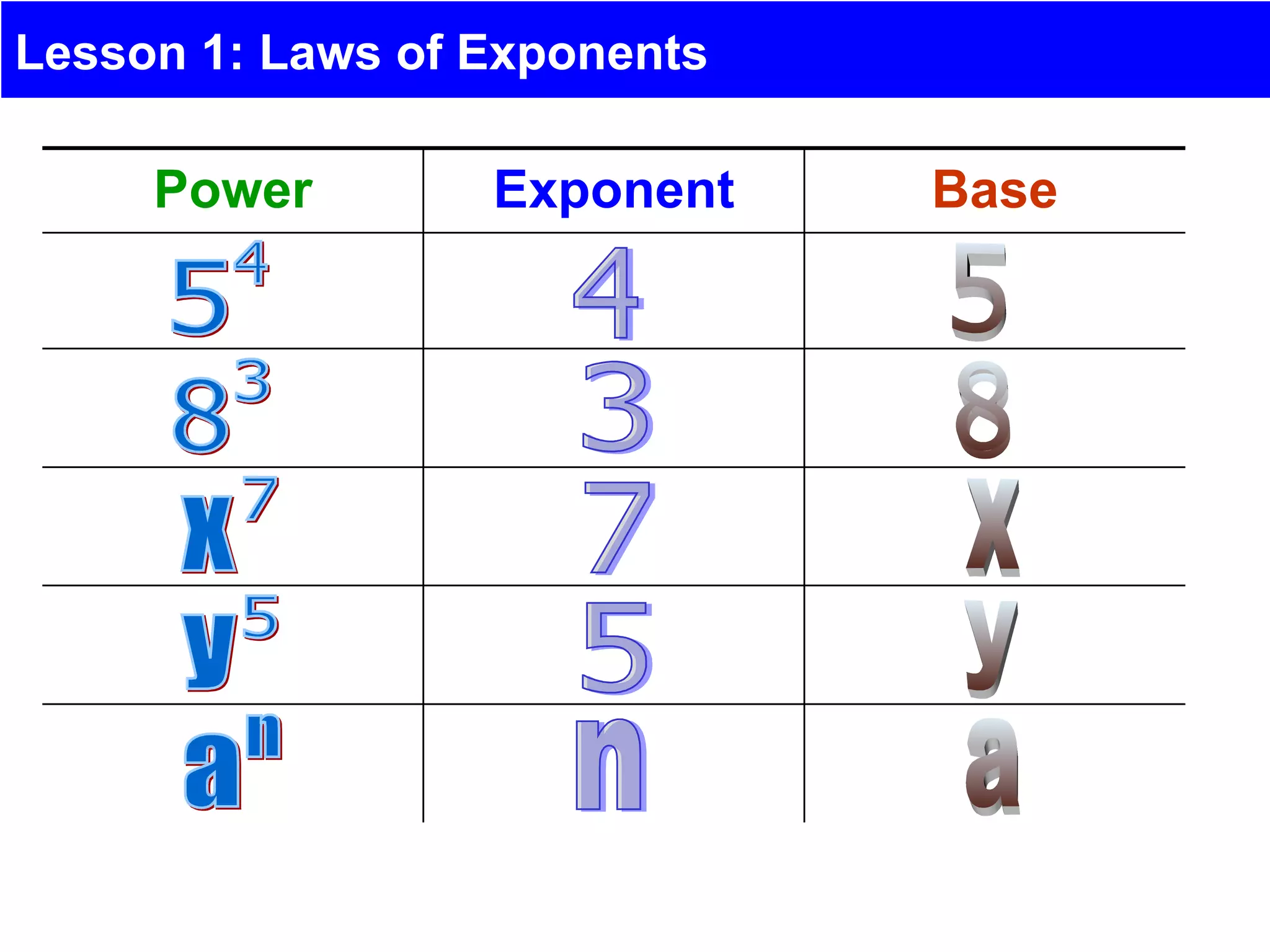
This document introduces the laws of exponents. It defines key terms like exponent, base, and power. It then outlines six laws of exponents: 1) the product law, 2) the quotient law, 3) the power law, 4) powers with different bases, 5) zero exponents, and 6) negative exponents. It concludes by explaining how to simplify powers and exponential expressions by applying these laws and definitions of exponents.
More Related Content
Laws Of Exponents
- 1. Laws of Exponents
- 2. Lesson 1: Lawsof Exponents Vocabulary exponent 7 2 base power
- 3. Lesson 1: Lawsof Exponents Power Exponent Base
- 4. Lesson 1: Lawsof Exponents Law 1: Product Law aman = am+n When multiplying two powers with the same base, just add the exponents.
- 5. Lesson 1: Lawsof Exponents Law 2: Quotient Law m a n = am-n a When dividing two powers with the same base, just subtract the exponents.
- 6. Lesson 1: Lawsof Exponents Law 2: Power Law (am)n = amn To simplify any power of power, simply multiply the exponents.
- 7. Lesson 1: Lawsof Exponents Powers with different bases anbn = (ab)n
- 8. Lesson 1: Lawsof Exponents Powers with different bases n n an = a b b Dividing different bases can’t be simplified unless the exponents are equal.
- 9. Lesson 1: Lawsof Exponents Zero exponents a =1 0 A nonzero base raised to a zero exponent Is equal to one.
- 10. Lesson 1: Lawsof Exponents Negative exponents 1 a-n = n a A nonzero base raised to a negative exponent is equal to the reciprocal of the base raised to the positive exponent.
- 11. Lesson 1: Lawsof Exponents Simplifying Powers A power is in its simplest form when the laws and definitions of exponents cannot be applied further to simplify it. Example: 4-3 not in simplest form 1 simplest form 64
- 12. Lesson 1: Lawsof Exponents Simplifying an Exponential Expression Exponential expressions are algebraic expressions which contain exponents. An algebraic expression is in simplest form when it is written with only positive exponents. If The expression is a fraction in simplest form, the only common factor of the numerator and denominator is 1.
- 13. Lesson 1: Lawsof Exponents Evaluating an Exponential Expression To evaluate means to substitute the given value/s to the variable/s of the expression and simplifying the expression.