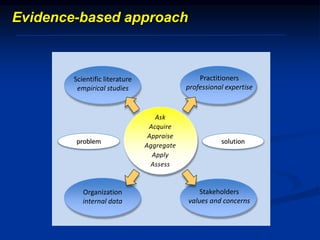
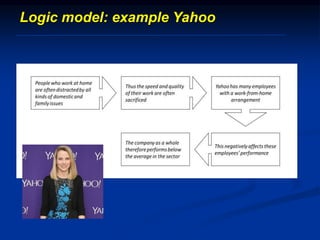
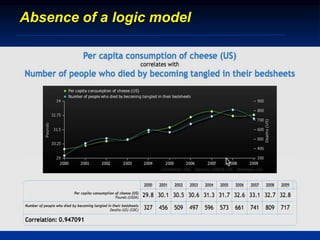
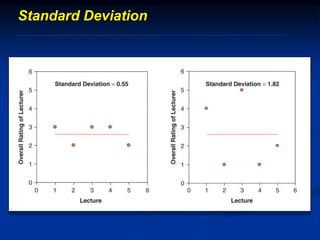
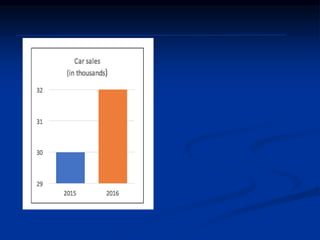
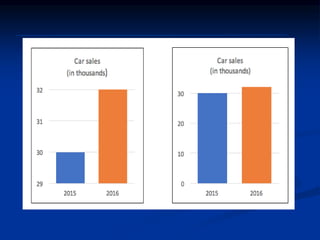
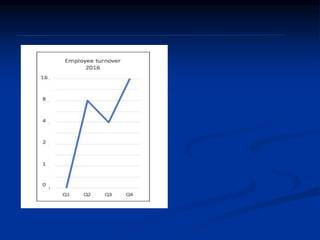
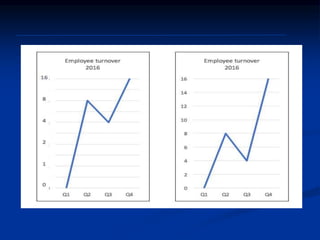
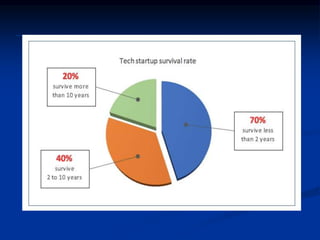
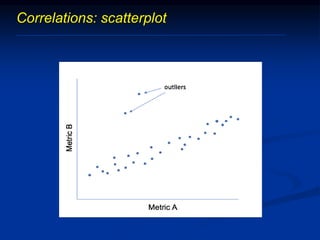
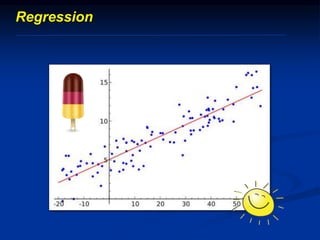
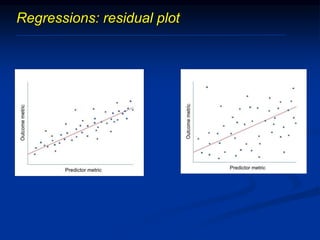
The document discusses several barriers students should be aware of when critically appraising organizational data, including: 1) the absence of a logic model, 2) garbage in/garbage out, 3) measurement errors, 4) small sample sizes, 5) confusing percentages and averages, 6) misleading graphs, and 7) issues with regression analysis like goodness of fit. It provides examples and definitions for each barrier to help students understand potential problems with organizational data and how to properly evaluate it.

1. Teaching students how to critically
appraise organizational data

2. Evidence-based approach
problem solution
Practitioners
professional expertise
Organization
internal data
Stakeholders
values and concerns
Scientific literature
empirical studies
Ask
Acquire
Appraise
Aggregate
Apply
Assess

4. Barriers students need to be aware of
1. Absence of a logic model
2. GIGO: Garbage In, Garbage Out
3. Measurement errors
4. Small numbers problem
5. Confusing percentages and averages
6. Misleading graphs
7. Goodness of fit
8. BIG data and other fancy stuff

5. Logic model: a definition
A logic model spells out the process by which we expect
underlying cause(s) to lead to a problem and produce
certain organizational consequences.
Think of a logic model as a short narrative explaining why
or when a problem occurs and how this leads to a
particular outcome.

6. Logic model

7. Logic model: example Yahoo

8. Absence of a logic model
Formulating a logic model prevents a ‘fishing
expedition’ in which a voluminous amount of data is
captured and exhaustively analyzed – an
inappropriate practice that increases the chance of
detecting non-existing relationships between the
variables.
A logic model help tie assumptions about problems
(or preferred solutions) to ‘real’ tangible relationships
linked by evidence

9. Absence of a logic model

10. 1. Absence of a logic model
2. GIGO: Garbage In, Garbage Out
3. Measurement errors
4. Small numbers problem
5. Confusing percentages and averages
6. Misleading graphs
7. Goodness of fit
8. BIG data and other fancy stuff
Barriers students need to be aware of

11. Garbage in garbage out
Unreliable data, inaccurate data, irrelevant data

12. Garbage in garbage out
Unreliable data, inaccurate data, irrelevant data

13. 1. Absence of a logic model
2. GIGO: Garbage In, Garbage Out
3. Measurement error
4. Small numbers problem
5. Confusing percentages and averages
6. Misleading graphs
7. Goodness of fit
8. BIG data and other fancy stuff
Barriers students need to be aware of

14. Measurement error
Whenever something is observed and measured
(from profit to intelligence), its score is likely to
deviate somewhat from its true score. This
deviation is measurement error (also known as
unreliability).
Nothing is measured perfectly

15. Measurement error
NB:
Two variables that are measured with little
error can be the origins of a variable with great
measurement error.
Measurement error tends to be greater where the variable is a
difference score (= one variable minus another). A difference
score has lower reliability than the two variables that compose
it when those two variables are positively correlated.

16. 1. Absence of a logic model
2. GIGO: Garbage In, Garbage Out
3. Measurement errors
4. Small numbers problem
5. Confusing percentages and averages
6. Misleading graphs
7. Goodness of fit
8. BIG data and other fancy stuff
Barriers students need to be aware of

17. A certain town is served by two hospitals. In the larger hospital
about 45 babies are born each day, and in the smaller hospital
about 15 babies are born each day. As you know, about 50% of
all babies are boys. However, the exact percentage varies from
day to day. Sometimes it may be higher than 50%, sometimes
more. For a period of 1 year, each hospital recorded the days on
which more than 60% of the babies born were boys. Which
hospital do you think recorded more such days?
1. The larger hospital
2. The smaller hospital
3. About the same (within 5% of each other)
4. I don’t know
Small numbers problem

18. Law of large numbers
The larger the sample size (or the number of
observations), the more accurate the predictions of the
characteristics of the whole population, and smaller
the expected deviation in comparisons of outcomes.

19. The small number problem often arises in
three situations:
1. When organizations compare units (e.g. teams,
departments or divisions) unequal in size.
2. When organizations collect data from a sample rather than
from the whole organization.
3. When organizations have access only to a small sample of
the total market population.

20. 1. Absence of a logic model
2. GIGO: Garbage In, Garbage Out
3. Measurement errors
4. Small numbers problem
5. Confusing percentages and averages
6. Misleading graphs
7. Goodness of fit
8. BIG data and other fancy stuff
Barriers students need to be aware of

21. A pharmaceutical company has tested a new,
experimental drug for Parkinson’s disease. Compared
with drugs currently prescribed, the new drug
decreases symptoms such as tremors, limb stiffness,
impaired balance and slow movement by 30 percent.
However, compared with the existing drugs, the
mortality rate of patients taking the new drug (those
dying because of serious side effects) has increased by
200 percent. Would you decide to bring this new drug
to the market?
Confusing percentages

22. Most people will be inclined to say no, because a 200
percent mortality rate increase sounds pretty
dramatic. However, this depends on the base value. If
the mortality rate of the existing drugs is only 1 in
350,000 patients (0.000003 percent), a relative
increase of 200 percent means an absolute increase of
only two in 350,000 patients (0.000006 percent). In all,
the new drug sounds like it has better outcomes,
especially as a patient’s improvement in health would
be substantial.
Confusing percentages

23. NOTE:
Whenever changes or differences are presented as
percentages, we must make clear whether these
differences are relative or absolute. Ideally both types
– including the number of standardized units they
represent – should be reported.
Confusing percentages

24. Confusing averages

25. Standard Deviation

26. Standard deviation > effect size
The standard deviation (often abbreviated SD) is also
helpful in determining the size of a change or difference.
If you take the percentage of change and divide it by the
standard deviation, you get a good impression of its
magnitude.
In the social sciences, a change of 0.2 is usually
considered a small difference, while 0.5 is considered a
moderate difference, and 0.8 is a large difference

27. Standard deviation > effect size
In the past four years, an Italian shoe factory has experienced multiple
restructurings and downsizings, reducing its workforce from 800 to
fewer than 500 factory workers. The HR Director believes that this has
been very stressful for the workers, causing a dramatic productivity
decline. He decides to introduce a stress-reduction program, including
on-site chair massage therapy.
A few months after the program is introduced, organizational data
indicate productivity has gone up: the workers average (mean)
productivity has increased by five percent from 200 shoes to 210
shoes per day, with a standard deviation of 7. A 5 percent change
equals 5/7 = .7 standard deviation, so this suggests that the program
may have had a large impact.

28. 1. Absence of a logic model
2. GIGO: Garbage In, Garbage Out
3. Measurement errors
4. Small numbers problem
5. Confusing percentages and averages
6. Misleading graphs
7. Goodness of fit
8. BIG data and other fancy stuff
Barriers students need to be aware of

35. 1. Absence of a logic model
2. GIGO: Garbage In, Garbage Out
3. Measurement errors
4. Small numbers problem
5. Confusing percentages and averages
6. Misleading graphs
7. Goodness of fit
8. BIG data and other fancy stuff
Barriers students need to be aware of

36. Correlations: scatterplot

37. Correlations: r-squared (variance explained)
To get a better idea of how strongly two metrics are correlated, we can
take a look at the r2 (pronounced “r-squared”). The r2 indicates the
extent variation or differences in one metric can be explained by a
variation or differences in a second metric. The r2 is expressed as a
percentage and can easily be calculated by squaring the correlation
coefficient.
For example, if the organizational data show that the correlation
between customer satisfaction and sales performance is r = .5, then the
r-squared is .25, indicating that 25 percent of the variation in sales
(increase or decrease) can be explained by a differences in customer
satisfaction.

38. Regression
Regression
Predicting an outcome variable from one predictor
variable (simple regression) or several predictor
variables (multiple regression)
Example
For every one degree rise in temperature,
1.18 more ice cream bars are sold on average

39. Regression

40. A regression coefficient tells you how much the outcome metric
is expected to increase (if the coefficient is positive) or
decrease (if the coefficient is negative) when the predictor
metric increases by one unit. There are two types of regression
coefficients: unstandardized and standardized. An
unstandardized coefficient concerns predictor and outcome
metrics that represent “real” units (e.g. sales per month, points
on a job satisfaction scale or numbers of errors). In that case,
the coefficient is noted as “b”.
For example, when a predictor metric temperature is regressed
on the number of ice creams sold, a regression coefficient of b
= 8.3 means that for every one degree rise in temperature, 8.3
more ice cream bars are sold on average.
Regression coefficients: unstandardized

41. A standardized coefficient involves predictor and outcome
metrics expressed in standard deviations. In that case, the
coefficient is noted as 𝛃 (pronounced as beta). Betas provide
information about the effect of the predictor metric on the
outcome metric. As explained in Chapter 7, in case of a simple
regression a 𝛃 of .10 is considered a small effect, whereas a
𝛃 of .60 is considered a large effect. In the case of a multiple
regression the thresholds are slightly higher (𝛃 = .20 is
considered small, 𝛃 = .80 is considered large).
Regression coefficients: standardized

42. Regressions: residual plot

43. Regressions: goodness of fit
In a regression analysis, the R2 tells us how close the
observed data are to the regression line. Put differently, it is
the percentage of the outcome metric that, based on the
regression coefficient, is predicted by the predictor metric.
For example, when the unstandardized regression coefficient
b for customer satisfaction and the number of sales is 30.2,
this indicates that for one point of improvement in the level of
customer satisfaction, on average 30.2 more products are
sold. However, when the R2 is only .18, this means that the
level of customer satisfaction can predict only 18 percent of
the number of sales.

44. 1. Absence of a logic model
2. GIGO: Garbage In, Garbage Out
3. Measurement errors
4. Small numbers problem
5. Confusing percentages and averages
6. Misleading graphs
7. Goodness of fit
8. BIG data and other fancy stuff
Barriers students need to be aware of

45. Big data, artificial intelligence, neural
networks, deep learning, etc.

47.  The number of medication errors in Unit 1 were 200%
greater in 2011 than Unit 2. Is patient safety worse in
Unit 1?
Let’s practice

48.  The number of medication errors in Unit 1 were 200%
greater in 2011 than Unit 2. Is patient safety worse in
Unit 1? Depends on number of unsafe incidents divided
by # patients or # procedures—needs a control
Let’s practice

49.  Unit 1 has 10 employees and 20% turnover while Unit 2
has 55 employees and 10% turnover. Is retention better
in Unit 1?
Let’s practice

50.  Unit 1 has 10 employees and 20% turnover while Unit 2
has 55 employees and 10% turnover. Is retention better
in Unit 1? Hard to determine. Small units tend to have
smaller numbers of observations, so its data might
contain more random error.
Let’s practice