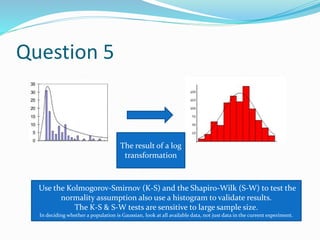
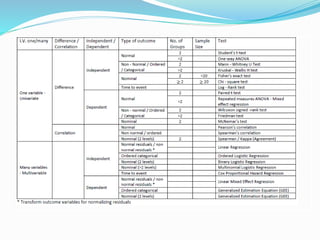
The document discusses sample size estimation and statistical test selection for data analysis in clinical trials. It emphasizes the importance of calculating sample size to achieve study objectives, avoid type I and II errors, and choose appropriate statistical tests based on study design and hypothesis. Various factors affecting sample size, such as effect size, allocation ratio, and the type of outcome, are detailed to guide researchers in their planning and reporting.

1. Sample Size estimation and a step-by-step approach for
choosing an appropriate statistical test for data analysis.
Vergoulas E.
Mathematician MSc
10th Scientific Conference Department of Medicine A.U.Th.
Round Table

2. Presentation Structure
 Sample size calculation
 Why?
 When?
 How?
 Study design & outcome of interest
 Error probabilities
 1 – tailed or 2 – tailed testing
 Effect size
 Allocation ratio – Losses
 Things to consider…
 Test selection
 Why it is important
 Selection procedure
 Selection Questions
 Multivariable Analysis
 Reporting for publishing
 References

3. Sample size calculation

4. Why?
 Ensures a high probability of the study achieving its
prespecified main objective
 In the absence of a priori sample size calculation there is no
knowledge of type I (false positive) and type II (false
negative) error.

5. When?
 Before the trial
 Can reduce the risk of an underpowered (false - negative) result in a well-
designed trial.
 Revision during the trial
 The study protocol should describe a comprehensive plan for the timing
and method of the potential modifications.
 Revisiting the sample size, without a formal statistical stopping rule, can
lead to the inflation of type I error so it is strongly advised to be avoided.
Similar problems can occur in larger than planned sample sizes.

6. How?
 Key components of sample size calculation
 Study design & outcome of interest
 Type I error or α (false positive) and Τype II error or β
(complement to power)
 1 – tailed or 2 – tailed testing
 Effect size or magnitude of the treatment effect
 Allocation ratio
 Losses

7. Study design & outcome of interest
 The approach of the hypothesis and questions asked define
the outcome of interest
 Moving from continuous to categorical outcome
measures increases sample size.
 Using non – parametric tests increases sample size.
 If there are secondary objectives they must be considered
during sample size calculation to ensure enough power
throughout the trial.

8. Error probabilities
 Type I error or α (false positive) and type II error or β
(false negative - complement to power)
Usually set at 5% and 20% respectively.
Deviations could happen based
on the nature of the study.
The smaller the probabilities
the larger the sample needed.

9. 1 – tailed or 2 – tailed testing
 Usually when comparing two treatments we do not
know in advance which is better.
Use of 2 – tailed test is recommended unless justified.
Two tailed testing requires larger samples.

10. Effect size
 “Effect size is a simple way of quantifying the size of
the difference between two groups”
 It is scale free, can be comparable among studies
 Effect size* of 0,5 corresponds to: 69% of the control group
would be below the average person in the experimental group.
 0,5 is considered large effect
 0,3 medium effect (62%)
 0,1 small effect (54%)
 Large effect size leads to smaller samples – small effect size leads
to larger samples.
* effect size for mean difference between two groups

11. Effect size
 To calculate effect size* we require
 H0 = the null hypothesis
 H1 = alternative hypothesis
 The standard deviation of the samples
* effect size for mean difference between two groups

12. Effect size
 It is not an estimation of the population parameters
per se, but the treatment effect deem worthy* of
detecting
 Sample size calculation is our best estimate of a
required sample size not the absolute truth
* Minimum Important Difference: Specifies the difference between treatments
that would lead clinicians to change practice.
VS
Minimum Detectable Difference (MDD) - can be specified given the significance
level, power and sample size.
Statistical Significance ≠ Clinical Importance

13. Effect size
JAMA editorial 2019
Clinical interventions in
 Psychiatry median effect size of 0,41
 General medicine median effect size of 0,37
“What seems prudent is that trials of any new treatment
should assume the median observed in the field, and
those who hope for a much larger effect size should be
required to provide a strong justification for such
optimism.”

14. Effect size
 Population Variability
(large variance = smaller effect size = larger sample size)
 In case of uncommon conditions or if recruitment is
conducted among multiple locations higher variability
(consider larger sample) and higher heterogeneity
(higher generalizability of results).

15. Allocation ratio - Losses
 Allocation ratio
The more we diverge from 1 the larger the sample size
required.
 Losses
Factors such as losses to follow – up, non – compliance,
drop – outs, missing data etc. should be taken under
consideration. The sample size should be inflated based
on previous experience.

16. Sensitivity analysis
Part of this analysis will address issues that may rise due
to assumptions made in order to calculate sample size
and consequently the validity of the trial conclusions.
Some common scenarios
 Distribution assumptions
 Missing data
 Non – compliance
 Outliers
 Variation
 Definition of outcomes

17. Things to consider…
 Reader confidence increases when reporting a detailed
 sample size calculation
 detailed plan of data analysis
 Sample size calculation is strongly associated with
power analysis so it can help with the interpretation of
study findings when statistically significant effects
are not found.
“The effect under study might exist but is lower than the expected
and so the current trial could not detect it, thus it is likely to be of
little clinical benefit.”

18. Things to consider…
 Clinical prediction models
(continuous, binary or time – to – event outcomes)
and the 10 events per variable (10 EPV).
Actually it is 10 events per predictor parameter (EPP) and
since some variables, such as a blood pressure with a
nonlinear effect requires two parameters to be modeled
caution is advised. Same for categorical variables with more
than two grades or for interactions.
For more details on the subject, we suggest the article by Riley et al. (BMJ, 2020)

19. Statistical test selection

20. Why test selection is important
 Selecting an inappropriate analysis undermines the
time and effort that go into doing rigorous research.
 Errors in test selection that leads to incorrect
inferences weaken our knowledge base in the field.
 New research based on inaccurate conclusions from
previous work, undermines the validity of the research
process as a whole.

21. Test Selection
To determine which test should be used in any given
circumstance, we need to consider:
 the hypothesis that is being tested
 the independent and dependent variables
 their scale of measurement
 the study design
 the assumptions of the test – test robustness
 sample distribution
 sample size

22. Question 1
“Univariate” or “Multivariable”
What are the independent and dependent variables?
 Univariate – Unadjusted Analysis
 Multivariable – Adjusted Analysis

23. Question 2
"Difference" or "Correlation“
Do we want to test for a difference between groups or we
want to test for correlation between variables?
- Comparing mean (or median) of two groups (or more)
- Correlation between two variables in one group

24. Question 3
"Paired" or "Independent“
Are we measuring more than once from one sample /
population? (repeated measures, linked selection, or matching)
Are we measuring from different samples / populations?

25. Question 4
“Type of Outcome“
 Discrete/Categorical
 Nominal (sex, gene present, outcome of treatment,
cancer type)
 Ordinal (education, pain level, disease severity)
 Continuous / Interval ( age, income, blood pressure)
We can transform continuous data to discrete but with
justification and cost in power.

26. Question 5
Is the distribution of the outcome variable Normal?
This is a statistical guideline published by New England
Journal of Medicine.
"Exact methods should be used as extensively as possible in
the analysis of categorical data. For analysis of
measurements, nonparametric methods should be used to
compare groups when the distribution of the dependent
variable (the outcome variable) is not normal".

27. Question 5
Using a parametric statistical test when it is not
appropriate can be problematic for several reasons.
 The analysis of the data may result in a rejection of the null
hypothesis, because one of the assumptions of the test is
invalid. Hypothesis tests in general are sensitive detectors
not only of false hypotheses but also of false assumptions
in the model.
 Sometimes the data indicate strongly that the null
hypothesis is false, and neutralize each other in the test, so
that the test reveals nothing and the null hypothesis is
accepted.

28. Question 5
Non - parametric test are not without assumptions.
 Sampling (random)
 Independence or dependence of samples (varies by test)
but make no assumptions about the population.

29. Question 5
The result of a log
transformation
Use the Kolmogorov-Smirnov (K-S) and the Shapiro-Wilk (S-W) to test the
normality assumption also use a histogram to validate results.
The K-S & S-W tests are sensitive to large sample size.
In deciding whether a population is Gaussian, look at all available data, not just data in the current experiment.

30. Question 6
“Number of Groups”
How many groups are there for the independent
(predictor) variable?
- 2 levels? (t-test, chi-square, Mann-Whitney U, Wilcoxon T )
- 3 levels or more? (ANOVA, chi-square, Kruskal-Wallis H Test,)

31. Multivariable Analysis
Only depends on:
1. Type of outcome variable
2. Are data paired/repeated or not
outcome continuous = linear regression
with repeated measures = mixed effect model regression
outcome binary = logistic regression
with repeated measures = generalized estimating equation
regression

33. Reporting for publishing
 Describe the purpose of the analysis
 Identify the variables used – summarize with
descriptive statistics
 Describe fully the methods of analysis
 Verify that the data conformed to the assumptions of
the test used.
 Name the statistical package used in the analysis
For more details on the subject we suggest:
1. Lang TA, Altman DG. Basic statistical reporting for articles published in biomedical journals: the
"Statistical Analyses and Methods in the Published Literature" or the SAMPL Guidelines.
2. https://www.equator-network.org/reporting-guidelines/

34. References and useful links
1. Bhatt DL, Mehta C. Adaptive Designs for Clinical Trials. N Engl J Med. 2016 Jul 7;375(1):65-74. doi:
10.1056/NEJMra1510061. PMID: 27406349
2. Chan A, Tetzlaff J M, Gatzsche P C, Altman D G, Mann H, Berlin J A et al. SPIRIT 2013 explanation and
elaboration: guidance for protocols of clinical trials. BMJ. 2013; 346 :e7586 doi:10.1136/bmj.e7586
3. Coe R. It’s the effect size, stupid: what effect size is and why it is important. Paper presented at: Annual
Conference of the British Educational Research Association; September 12-14, 2002; Exeter, England.
http://www.leeds.ac.uk/educol/documents /00002182.htm. Accessed April 4, 2021.
4. Cook J A, Julious S A, Sones W, Hampson L V, Hewitt C, Berlin J A et al. DELTA2 guidance on choosing the
target difference and undertaking and reporting the sample size calculation for a randomised controlled
trial BMJ 2018; 363 :k3750 doi:10.1136/bmj.k3750
5. Dahiru T. (2008). P - value, a true test of statistical significance? A cautionary note. Annals of Ibadan
postgraduate medicine, 6(1), 21–26. https://doi.org/10.4314/aipm.v6i1.64038
6. Farrokhyar F, Reddy D, Poolman RW, Bhandari M. Why perform a priori sample size calculation? Can J Surg.
2013 Jun;56(3):207-13. doi: 10.1503/cjs.018012. PMID: 23706850; PMCID: PMC3672437
7. Kapur S, Munafò M. Small Sample Sizes and a False Economy for Psychiatric Clinical Trials. JAMA Psychiatry.
2019;76(7):676–677. doi:10.1001/jamapsychiatry.2019.0095
8. Kenneth F Schulz, David A Grimes, Sample size calculations in randomized trials: mandatory and mystical,
The Lancet, Volume 365, Issue 9467,2005, Pages 1348-1353, ISSN 0140-6736,
https://doi.org/10.1016/S0140-6736(05)61034-3
9. Krousel-Wood, M. A., Chambers, R. B., & Muntner, P. (2007). Clinicians' Guide to Statistics for Medical
Practice and Research: Part II. The Ochsner journal, 7(1), 3–7.
10. Lang TA, Altman DG. Basic statistical reporting for articles published in biomedical journals: the "Statistical
Analyses and Methods in the Published Literature" or the SAMPL Guidelines. Int J Nurs Stud. 2015
Jan;52(1):5-9. doi: 10.1016/j.ijnurstu.2014.09.006. Epub 2014 Sep 28. PMID: 25441757.

35. References and useful links
10. Riley R D, Ensor J, Snell K I E, Harrell F E, Martin G P, Reitsma J B et al. Calculating the sample size required
for developing a clinical prediction model BMJ 2020; 368 :m441 doi:10.1136/bmj.m441
11. Sedgwick P. Randomised controlled trials: the importance of sample size. BMJ 2015;350:h1586 doi:
https://doi.org/10.1136/bmj.h1586
12. Stokes L. Sample size calculation for a hypothesis test. JAMA. 2014 Jul;312(2):180-1. doi:
10.1001/jama.2014.8295. PMID: 25005655
13. Thabane, L., Mbuagbaw, L., Zhang, S. et al. A tutorial on sensitivity analyses in clinical trials: the what, why,
when and how. BMC Med Res Methodol 13, 92 (2013). https://doi.org/10.1186/1471-2288-13-92
14. Yuan I, Topjian AA, Kurth CD, Kirschen MP, Ward CG, Zhang B, Mensinger JL. Guide to the statistical
analysis plan. Paediatr Anaesth. 2019 Mar;29(3):237-242. doi: 10.1111/pan.13576. Epub 2019 Jan 29.
PMID: 30609103.
Links
1. https://stats.idre.ucla.edu/other/mult-pkg/whatstat/
2. https://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one/13-study-design-
and-choosing-statisti
3. http://www.biostathandbook.com/testchoice.html
4. http://rcompanion.org/handbook/D_03.html
5. http://www.wadsworth.com/psychology_d/templates/student_resources/workshops/stat_workshp/chos
e_stat/chose_stat_01.html
6. https://www.psychologie.hhu.de/arbeitsgruppen/allgemeine-psychologie-und-arbeitspsychologie/gpower
7. https://www.equator-network.org/reporting-guidelines/

36. Thank You!