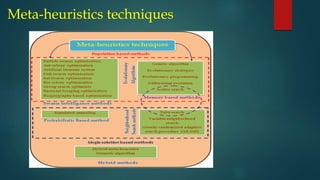
The document provides an overview of Tabu Search (TS) as a meta-heuristic optimization technique proposed by Glover in 1986, highlighting its popularity in solving various optimization problems. Key concepts discussed include the use of memory through a tabu list to avoid revisiting solutions and the method's acceptance of non-improving solutions to escape local optima. Additionally, the document outlines examples and applications of TS in fields like scheduling, vehicle routing, and resource allocation.

1. Tabu Search
DR. AHMED FOUAD ALI
FACULTY OF COMPUTERS AND INFORMATICS
SUEZ CANAL UNIVERSITY

2. Meta-heuristics techniques

3. Outline
2. Tabu search (TS)(Background)
3. TS (main concepts)
5. TS examples
4. TS algorithm
6. TS applications
1. Motivation

4. Motivation
starting
point
descend
direction
local minima
global minima
barrier to local search
?
?

5. Tabu search (TS)(Background)
• Tabu search (TS) algorithm was proposed by Glover
(1986).
•In the 1990s, the tabu search algorithm became very
popular in solving optimization problems.
•Nowadays, it is one of the most wide spread (single )
S-metaheuristics.
•The use of memory represents the particular feature
of tabu search.
•TS behaves like a steepest LS algorithm, but it accepts
nonimproving solutions to escape from local optima.

6. Tabu search (main concepts)
• The key feature of TS method is the use
of memory, which records information
related of the search process.
•TS generates a neighborhood solution
from the current solution and accepts the
best solution even if is not improving the
current solution.
This strategy may lead to cycles
i.e the previous visited solutions could
be selected again.

7. Tabu search (main concepts)
• In order to avoid cycles, TS discards the
solution that have been previously visited
by using memory which is called tabu list.
•The length of the memory (tabu list)
control the search process.
•A high length of the tabu list is high the
search will explore larger regions and
forbids revisiting high number of solution.
•A low length of the tabu list concentrates
the search on a small area of the search
space.

8. Tabu search (main concepts)
• At each iteration the tabu list is
updated (first in – first out queue).
•The tabu list contains a constant
number of tabu moves called tabu
tenure, which is the length of time for
which a move is forbidden.
•If a move is good and can improve the
search process but it is in tabu list, there
is no need to be prohibited and the
solution is accepted in a process called
aspiration criteria.

9. Tabu search algorithm

10. Tabu search examples
x0
N(x0) X0 Neighborhood
trail solutions
x1
N(x1)
x2
x3
x4
x14
x15
x16

11. TS examples
1||SwjTj
Jobs 1 2 3 4
wj 4 5 3 5
pj 12 8 15 9
dj 16 26 25 27
 Determine Sc by the best schedule in the
neighborhood that is not tabu
 Use tabu-list length = 2
– The tabu list is denoted by L

12. TS examples
 Step 1: S0=S1=(1,3,2,4). G(S1)=136. Set L={}.
 Step 2. N(S1)= {(3,1,2,4), (1,2,3,4), (1,3,4,2)}
with respective cost = {174, 115, 141} =>
Sc=S0=S2=(1,2,3,4).
Set L={(3,2)}, i.e., swapping 3 and 2 is not
allowed (Tabu)
 Step 3: Let k=2
Iteration 1

13. TS examples
 Step 2.
– N(S2)= {(2,1,3,4), (1,3,2,4), (1,2,4,3)}
– with respective costs = {131, - , 67}
– => Sc=S3=(1,2,4,3)
– Set S0=Sc
– Set L={(3,4),(3,2)}
 Step 3: Let k=3
Iteration 2
X

14. TS examples
 Step 2
– N(S3)= {(2,1,4,3), (1,4,2,3), (1,2,3,4)}
– with respective costs = {83, 72, -}
– => Sc=S4=(1,4,2,3)
– Set L={(2,4),(3,4)}
 Step 3: Let k=4
Iteration 3
X

15. TS examples
 Step 2
– N(S4)= {(4,1,2,3), (1,2,4,3), (1,4,3,2)}
– with respective costs = {92, -, 123}
– => Sc=S5=(4,1,2,3)
– Set L={(1,4),(2,4)}
 Step 3: Let k=5
Iteration 4
X

16. TS examples
 Step 2
– N(S5)= {(1,4,2,3), (4,2,1,3), (4,1,3,2)}
– with respective costs = {-, 109, 143}
– => Sc=S6=(4,2,1,3)
– Set L={(2,1),(4,1)}
 Step 3: Let k=6
Iteration 5
X

17. TS Applications
Scheduling Quadratic
assignment
Frequency
assignment
Car pooling Capacitated
p-median,
Resource
constrained project
scheduling (RCPSP)
Vehicle
routing
problems
Graph
coloring
Retrieval
Layout
Problem
Maximum
Clique
Problem,
Traveling Salesman
Problems
Database
systems
Nurse
Rostering
Problem
Neural Nets Grammatical
inference,
Knapsack problems SAT
Constraint
Satisfaction
Problems
Network
design
Telecomunicati
on Network
Global
Optimization

18. References
Metaheuristics From design to implementation, El-Ghazali
Talbi, University of Lille – CNRS – INRIA.
F. Glover, Future paths for integer programming and links to
artificial intelligence, Computers and Operations Research 13
(1986), 533-549.