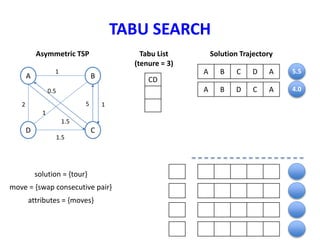
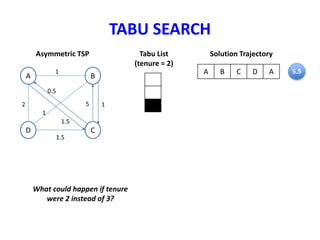
Tabu search is a metaheuristic algorithm used to solve optimization problems. It guides a local search procedure to explore the solution space beyond local optimality. Tabu search uses short-term memory, in the form of a tabu list, to avoid getting stuck in cycles. The tabu list stores attributes of recently visited solutions and makes those attributes "taboo" or forbidden for some number of iterations. This helps the search process escape local optima and explore new regions of the solution space. The size of the tabu tenure can be adjusted to control the tradeoff between intensification of the search and diversification.

1. Metaheuristic Algorithm
Presented by:
Lames Alhilali
Supervisor:
Dr. wedad Alsorori

2. • Optimization Problems
• Strategies for Solving NP-hard Optimization Problems
(Non-deterministic Polynomial)
• What is a Metaheuristic Method?
• Trajectory Methods
• The Applications of Metaheuristic Methods

3. REFERENCES
• Talbi E.-G., 2009. Metaheuristics: from design to
implementation, Vol. 74, John Wiley & Sons
• Blum C. and Roli A., 2003. Metaheuristics in
combinatorial optimization: Overview and conceptual
comparison, ACM Computing Surveys, 35(3):268-308
• Back T., Hammel U. and Schwefel H.-P., 2002.
Evolutionary computation: comments on the history
and current state, IEEE Transactions on Evolutionary
Computation, 1(1):3-17

4. Optimization Problems
Computer Science:
 Traveling Salesman Problem
Operational Research (OR):
• P-Median Problem (location selection)
Many optimization problems are NP-hard.

5. An example: TSP
(Traveling Salesman Problem)
18
1
2
3
5
4
23
10 5
3
7
15
20
6
A solution A sequence
12345 Tour length = 31
13452 Tour length = 63
There are (n-1)! tours in total

6. • Let’s consider the problem of find the best
visiting sequence (route) to serve 14
customers.
• How many possible routes exists?
– (n-1)!=(15-1)!=14!= 8,7178 X 1010 = 88 billion
solutions
– If a PC can check about 1 million solution per
second, then we need 8,8*1010 routes /106
routes/ sec = 88.000 sec or about 24,44 hours to
check them all and find the best!

7. COMBINATORIAL EXPLOSION
• What type of algorithm would you pick to solve a
problem with 1049,933 feasible solutions?
13,509-city TSP
19,982.859 mi.

8. Strategies for Solving NP-hard
Optimization Problems
• Branch-and-Bound (B&B)  Finds an exact solution
These algorithms aim to find the optimal solution by
exhaustively searching through all possible solutions.
computationally expensive and time-consuming, especially
for large problem instances.
• Approximation Algorithms
– There is an approximation algorithm for TSP which can find a
tour with tour length ≦ 1.5× (optimal tour length) in O(n3)
time, where n is the number of cities and the running time of
the algorithm grows cubically with the number of cities.
– provide solutions that are close to the optimal solution, but
not guaranteed to be the best. They provide a trade-off
between solution quality and computational efficiency.

9. Strategies for Solving NP-hard
Optimization Problems
• Heuristic Methods  Deterministic
- are designed to quickly find good solutions, although
they may not guarantee finding the absolute best solution. These
algorithms use rules of problem-specific knowledge to guide the
search for a good solution.
• Metaheuristic Methods  Heuristic + Randomization
– are higher-level strategies that guide the search process by using more
general techniques.

10. What is a Metaheruistic Method?
• Meta : in an upper level
• Heuristic : to find
A metaheuristic is formally defined as an iterative generation
process which guides a subordinate heuristic by combining
intelligently different concepts for exploring and exploiting the
search space, learning strategies are used to structure
information in order to find efficiently near-optimal solutions.

11. Fundamental Properties of Metaheuristics
• Metaheuristics are strategies that “guide” the search
process.
• The goal: is to efficiently explore the search space in
order to find (near-)optimal solutions.
• Techniques which constitute metaheuristic algorithms
range from simple local search procedures to complex
learning processes.
• Metaheuristic algorithms are approximate and usually
non-deterministic.

12. Fundamental Properties of Metaheuristics
• Metaheuristics are not problem-specific.
• Today’s more advanced metaheuristics use search
experience (embodied in some form of memory) to guide
the search.
Types of metahuristic algorithms:
 Genetic Algorithms (GA)
Particle Swarm Optimization (PSO)
Ant Colony Optimization (ACO)
Simulated Annealing (SA)
Tabu Search (TS)
Variable Neighborhood Search (VNS)

13. TABU SEARCH
• Taboo (English): prohibited, disallowed,
forbidden
• Tabu (Fijian): forbidden to use due to being
sacred and/or of supernatural powers
• …related to similar Polynesian words
tapu (Tongan), tapu (Maori), kapu (Hawaiian)

14. TABU SEARCH
• Used mainly for discrete problems
• The tabu list constitutes “short-term memory”
• Size of tabu list (“tenure”) is finite
• Since solutions in tabu list are off-limits, it helps
– escape local minima by forcing uphill moves (if no improving
move available)
– avoid cycling (up to the period induced by tabu list size)
• Solutions enter and leave the list in a FIFO order (usually)

15. TABU SEARCH
• Small tenure localizes search (intensification)
• Large tenure forces exploration of wider space
(diversification)
• Tenure can change dynamically during search
• Size of tenure is a form of “long-term
memory”

16. TABU SEARCH
• Storing complete solutions is inefficient
– implementation perspective (storage, comparisons)
– algorithm perspective (largely similar solutions
offer no interesting information)
• Tabu search usually stores “solution attributes”
– solution components or solution differences
(“moves”)

17. TABU SEARCH
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
Tabu List
(tenure = 3)
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
A B
D C
1
1
1
2
1.5
5
0.5
1.5

18. TABU SEARCH
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
B A C D B 5.0
A C B D A 9.5
A B D C A 4.0
D B C A D 4.5
Tabu List
(tenure = 3)
AB
BC
CD
DA
A B
D C
1
1
1
2
1.5
5
0.5
1.5

19. TABU SEARCH
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
B A C D B 5.0
A C B D A 9.5
A B D C A 4.0
D B C A D 4.5
Tabu List
(tenure = 3)
AB
BC
CD
DA
A B D C A 4.0
A B
D C
1
1
1
2
1.5
5
0.5
1.5

20. TABU SEARCH
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
Tabu List
(tenure = 3)
CD
A B D C A 4.0
A B
D C
1
1
1
2
1.5
5
0.5
1.5

21. TABU SEARCH
A B
D C
1
1
1
2
1.5
5
0.5
1.5
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
Tabu List
(tenure = 3)
CD
A B D C A 4.0
B A D C A 5.0
A D B C A 4.5
A B C D A
C B D A C 9.5
AB
BD
DC
CA
5.5

22. TABU SEARCH
A B
D C
1
1
1
2
1.5
5
0.5
1.5
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
Tabu List
(tenure = 3)
BD
CD A B D C A 4.0
B A D C A 5.0
A D B C A 4.5
A B C D A
C B D A C 9.5
AB
BD
DC
CA
5.5
A D B C A 4.5

23. TABU SEARCH
A B
D C
1
1
1
2
1.5
5
0.5
1.5
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
Tabu List
(tenure = 3)
BD
CD A B D C A 4.0
D A B C D
A B D C A
A D C B A
C D B A C
AD
DB
BC
CA
A D B C A 4.5
5.5
4.0
5.0
9.5

24. TABU SEARCH
A B
D C
1
1
1
2
1.5
5
0.5
1.5
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
Tabu List
(tenure = 3)
BD
CD A B D C A 4.0
D A B C D
A B D C A
A D C B A
C D B A C
AD
DB
BC
CA
A D B C A 4.5
5.5
4.0
5.0
9.5

25. TABU SEARCH
A B
D C
1
1
1
2
1.5
5
0.5
1.5
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
Tabu List
(tenure = 3)
CA
BD
CD
A B D C A 4.0
D C B A D
C B D A C
C D A B C
A D B C A
CD
DB
BA
AC
A D B C A 4.5
9.5
9.5
4.5
5.5
C D B A C 5.0

26. TABU SEARCH
A B
D C
1
1
1
2
1.5
5
0.5
1.5
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
Tabu List
(tenure = 3)
CA
BD
CD
A B D C A 4.0
D C B A D
C B D A C
C D A B C
A D B C A
CD
DB
BA
AC
A D B C A 4.5
9.5
9.5
4.5
5.5
C D B A C 5.0

27. TABU SEARCH
A B
D C
1
1
1
2
1.5
5
0.5
1.5
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
Tabu List
(tenure = 3)
BA
CA
BD
A B D C A 4.0
D C A B D
C A D B C
C D B A C
B D A C B
CD
DA
AB
BC
A D B C A 4.5
4.0
4.5
9.5
5.0
C D B A C 5.0
C D A B C 5.5

28. TABU SEARCH
Asymmetric TSP
A B C D A
Solution Trajectory
11
Tabu List
(tenure = 3)
attributes = {moves}
solution = {tour}
move = {swap consecutive pair}
A B
D C
2
2
2
4
3
10
1
3
What could happen if tenure
were 2 instead of 3?
What could happen if tenure
were 4 instead of 3?

29. TABU SEARCH
A B
D C
1
1
1
2
1.5
5
0.5
1.5
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
Tabu List
(tenure = 2)
What could happen if tenure
were 2 instead of 3?

30. TABU SEARCH
A B
D C
1
1
1
2
1.5
5
0.5
1.5
Asymmetric TSP
A B C D A
Solution Trajectory
5.5
Tabu List
(tenure = 4)
What could happen if tenure
were 4 instead of 3?

31. TABU SEARCH
• Decreasing tenure provides for intensification,
though encourages cycling
• Increasing tenure provides for diversification
by encouraging uphill moves
• How would you design a good TS algorithm?

32. TABU SEARCH
• Forbidding “attributes” may be overly restrictive
– aspiration conditions are introduced as “wild-cards”
for certain solutions, e.g., new incumbents are always
accepted, even if they possess taboo attributes

33. Comparison between heuristic and
metaheuristic algorithms

34. Research used this Algorithm
• Metaheuristic algorithms for a sustainable agri-food
supply chain considering marketing practices under
uncertainty.
• Year: Oct, 2022.
• Researcher: Fatemeh Gholian-Jouybari , Omid Hashemi-
Amiri, Behzad Mosallanezhad, Mostafa Hajiaghaei-Keshteli.
• Objectives :
– To develop and propose metaheuristic algorithms for optimizing
the agri-food supply chain.
– To consider marketing practices within the optimization
framework.
– To evaluate the performance and effectiveness of the proposed
algorithms.
• Link of study: https://www.sciencedirect.com/science/ar
• ticle/abs/pii/S095741742201898X

35. Research used this Algorithm
• A Tutorial On the design, experimentation and application of
metaheuristic algorithms to real-World optimization problems
• Year: Juk, 2021.
• Researcher: Eneko Osaba a, Esther Villar-Rodriguez a, Javier Del Ser
a b, Antonio J. Nebro d, Daniel Molina c, Antonio LaTorre g,
Ponnuthurai N. Suganthan f, Carlos A. Coello Coello e, Francisco
Herrera
• Objectives:
– To provide an overview of metaheuristic algorithms and their
applications in solving optimization problems.
– To explain the design principles and components of metaheuristic
algorithms, including problem representation, solution representation,
search operators, and termination criteria.
• Link of study:
https://www.sciencedirect.com/science/article/abs/pii/S221065022
1000493

36. Research used this Algorithm
• Solar energy forecasting based on hybrid neural network and
improved metaheuristic algorithm
• Year: Oct, 2017.
• Researcher: Oveis Abedinia, Nima Amjady, Noradin Ghadimi
• Objectives:
– To design and implement a hybrid forecasting model that combines
the strengths of a neural network and a metaheuristic algorithm.
– To improve the performance of the metaheuristic algorithm by
proposing novel enhancements or modifications.
– To evaluate and validate the proposed forecasting model using real-
world data.
– To contribute to the field of renewable energy management and grid
integration. Accurate solar energy forecasting is crucial for optimizing
the integration of solar power into the electrical grid.
• Link of study:
https://onlinelibrary.wiley.com/doi/abs/10.1111/coin.12145

37. Question
There is many types of metahuristic algorithms.
Mention three of them.
Genetic Algorithms (GA)
Tabu Search (TS)
Particle Swarm Optimization (PSO)
Ant Colony Optimization (ACO)
Simulated Annealing (SA)
Variable Neighborhood Search (VNS)

38. THANK YOU
Presented by:
LAMES ALHILALI