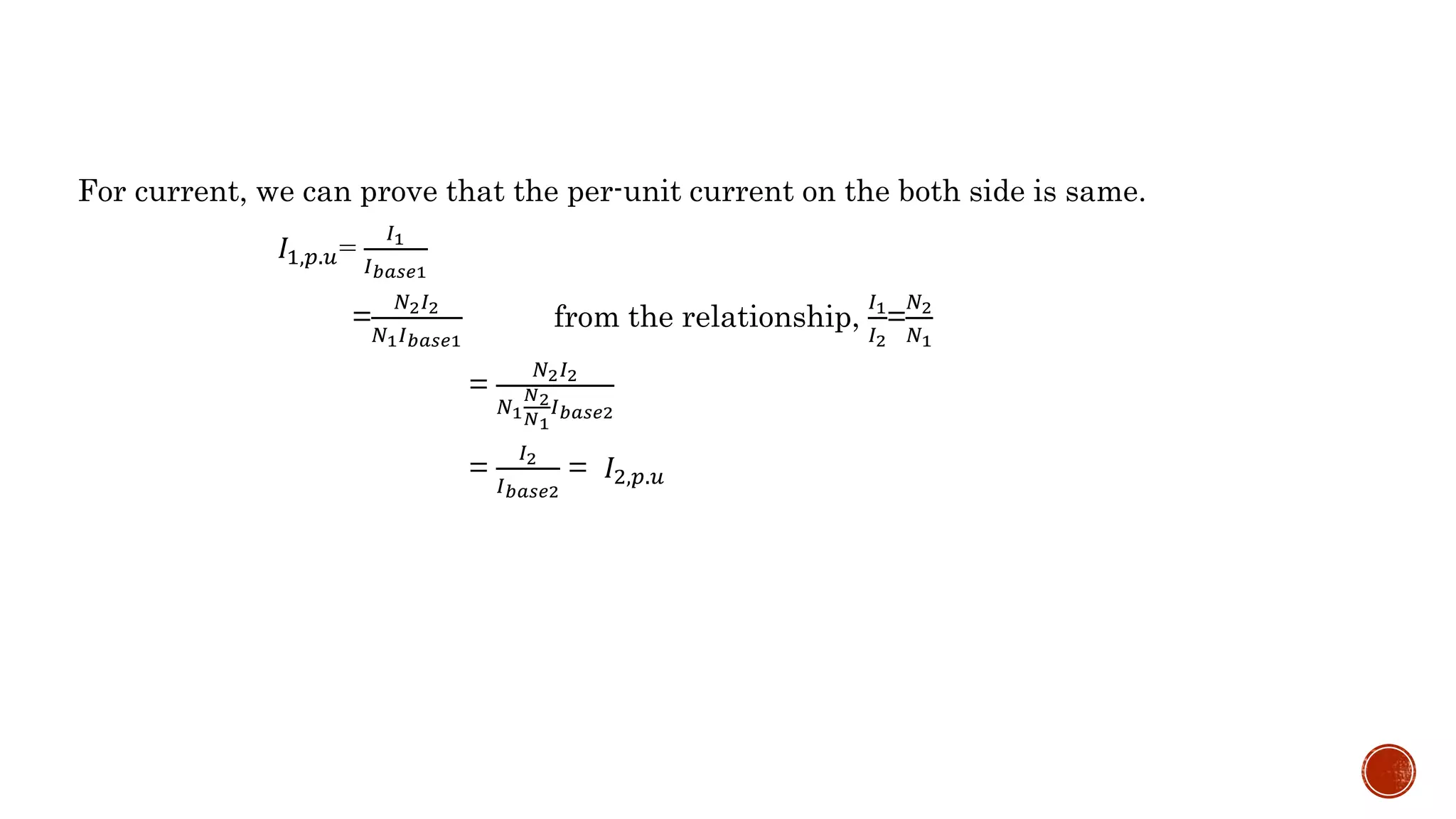
This document discusses per unit systems and symmetrical components for power system analysis. It defines a per unit system as expressing quantities as fractions of a defined base unit to simplify calculations when referring values across transformers. Advantages of per unit systems include similar impedances for similar apparatus and improved numerical stability. The document also defines symmetrical components as representing unbalanced three-phase quantities as the sum of three balanced components to analyze unbalanced faults.

1. Per Unit System
and
Symmetrical Component

2. Content
Per Unit system
 Definition
 Advantages
 Mathematical Relationship

3. Definition
 In the power systems analysis field of electrical engineering, a per-unit system is the expression of system
quantities as fractions of a defined base unit quantity.
 Calculations are simplified because quantities expressed as per-unit do not change when they are referred
from one side of a transformer to the other.
 The main idea of a per unit system is to absorb large difference in absolute values into base relationships.
Thus, representations of elements in the system with per unit values become more uniform.

4. Advantages of per-unit system
 Similar apparatus (generators, transformers, lines) will have similar per-unit impedances and losses expressed
on their own rating, regardless of their absolute size. Because of this, per-unit data can be checked rapidly for
gross errors. A per unit value out of normal range is worth looking into for potential errors.
 Manufacturers usually specify the impedance of apparatus in per unit values.
 Use of constant 3 is reduced in three-phase calculations.
 It improves numerical stability of automatic calculation methods.

5. By convention, we adopt the following two rules for base quantities:
 The value of base power is the same for the entire power system of concern.
 The ratio of the voltage bases on either side of a transformer is selected to be the same as the ratio of the
transformer voltage ratings.
Relationship between units
The relationship between units in a per-unit system depends on whether the system is single-phase or three-
phase.
 single Phase
Assuming that the independent base values are power and voltage, we have:
𝑃𝑏𝑎𝑠𝑒=1pu
𝑉𝑏𝑎𝑠𝑒=1pu

6. Alternatively, the base value for power may be given in terms of reactive or apparent power. In such case we
have, respectively:
𝑄 𝑏𝑎𝑠𝑒=1pu or 𝑆 𝑏𝑎𝑠𝑒=1pu
The rest of the units can be derived from power and voltage using the equations :
S=VI, P=Scos(ϕ), Q=Ssin(ϕ) and V=IZ, where Z is represented by:
Z=R+jX = Zcos(ϕ)+jXsin(ϕ), we have:
I 𝑏𝑎𝑠𝑒 =
𝑆 𝑏𝑎𝑠𝑒
𝑉 𝑏𝑎𝑠𝑒
= 1pu
Z 𝑏𝑎𝑠𝑒 =
𝑉 𝑏𝑎𝑠𝑒
𝐼 𝑏𝑎𝑠𝑒
=
𝑉2
𝑏𝑎𝑠𝑒
I 𝑏𝑎𝑠𝑒 𝑉 𝑏𝑎𝑠𝑒
=1pu
Y𝑏𝑎𝑠𝑒 =
1
Z 𝑏𝑎𝑠𝑒
=1pu

7.  Three Phase System
Power and voltage are specified in the same way as single-phase systems. However, the relationships for
the derived units are different. Specifically, power is given as total (not per-phase) power, and voltage is
line-to-line voltage. In three-phase systems the equations:
𝑄 𝑏𝑎𝑠𝑒=1pu and 𝑆 𝑏𝑎𝑠𝑒=1pu. The apparent power S now, 𝑆 𝑏𝑎𝑠𝑒= 3V𝑏𝑎𝑠𝑒I 𝑏𝑎𝑠𝑒
I 𝑏𝑎𝑠𝑒=
𝑆 𝑏𝑎𝑠𝑒
3V 𝑏𝑎𝑠𝑒
=1pu
Z 𝑏𝑎𝑠𝑒=
𝑉 𝑏𝑎𝑠𝑒
3I 𝑏𝑎𝑠𝑒
=
𝑉2
𝑏𝑎𝑠𝑒
𝑆 𝑏𝑎𝑠𝑒
=1pu
Y𝑏𝑎𝑠𝑒=
1
Z 𝑏𝑎𝑠𝑒
=1pu

8. In transformers
 The voltages, currents, and impedances in a per-unit system will have the same values whether they are
referred to primary or secondary of a transformer.
 For instance, for voltage, we can prove that the per unit voltages of two sides of the transformer, side 1 and
side 2, are the same. Here, the per-unit voltages of the two sides are E1p.u. and E2p.u. respectively.
𝐸1,𝑝.𝑢=
𝐸1
𝑉 𝑏𝑎𝑠𝑒1
=
𝑁1 𝐸2
𝑁2 𝑉 𝑏𝑎𝑠𝑒1
from the relationship,
𝐸1
𝐸2
=
𝑁1
𝑁2
=
𝑁1 𝐸2
𝑁2
𝑁1
𝑁2
𝑉 𝑏𝑎𝑠𝑒2
from the relationship,
𝑉1
𝑉2
=
𝑁1
𝑁2
=
𝐸2
𝑉 𝑏𝑎𝑠𝑒2
= 𝐸2,𝑝.𝑢

9. For current, we can prove that the per-unit current on the both side is same.
𝐼1,𝑝.𝑢=
𝐼1
𝐼 𝑏𝑎𝑠𝑒1
=
𝑁2 𝐼2
𝑁1 𝐼 𝑏𝑎𝑠𝑒1
from the relationship,
𝐼1
𝐼2
=
𝑁2
𝑁1
=
𝑁2 𝐼2
𝑁1
𝑁2
𝑁1
𝐼 𝑏𝑎𝑠𝑒2
=
𝐼2
𝐼 𝑏𝑎𝑠𝑒2
= 𝐼2,𝑝.𝑢

10. Three-Component method

11.  Charles Legeyt Fortescue (1918): Any set of N unbalanced phasors can be replaced
by N sets of balanced phasors.
 Fortescue demonstrated that any set of unbalanced three-phase quantities could
be expressed as the sum of three symmetrical sets of balanced phasors.
 Using this tool, unbalanced system conditions, like those caused by common fault
types may be visualized and analyzed.
 It is used for any number of phases but mainly used for the three-phase system.

12.  Whenever there is an unsymmetrical fault in an electrical system, the electrical
system becomes unbalanced.
 Than it becomes difficult to do per phase analysis because the three phases are
unequal and unbalanced.
 So to study unsymmetrical system per phase basis Symmetrical Component is
used.

13. Va = Va0 + Va1 + Va2
Vb = Vb0 + Vb1 + Vb2
Vc = Vc0 + Vc1 + Vc2
Va0 ; Vb0 ; Vc0 = Zero Sequence Component
Va1 ; Vb1 ; Vc1 = Positive Sequence Component
Va2 ; Vb2 ; Vc2 = Negative Sequence Component
V
aVc
Vb
abc

14. Vb1
Vc1
Va1
Positive Phase
Sequence
(abc)
Vb2
Vc2
Va2
Negative Phase Sequence
(acb)
Zero Phase Sequence
Va0 = Vb0 = Vc0 = Equal Magnitude
Unbalanced Phase Sequence = Zero Sequence + Positive Sequence + Negative Sequence

15. Within Fortescue’s formulas, the “α” operator shifts a vector by an angle of 120 degrees counter-
clockwise, and the “α 2 ” operator performs a 240 degrees counter-clockwise phase shift.
α = 1∠120°

16. Va = Va0 + Va1 + Va2
Vb = Vb0 + Vb1 + Vb2
Vc = Vc0 + Vc1 + Vc2
Va0 = Vb0 = Vc0 = Equal Magnitude
Vb1= α 2Va1
Vc1= α Va1
Va1
Positive Phase
Sequence
(abc)
Vb2 = α Va2
Vc2 = α 2Va2
Va2
Negative Phase Sequence
(acb)

17. Va = Va0 + Va1 + Va2
Vb = Vb0 + Vb1 + Vb2
Vc = Vc0 + Vc1 + Vc2
Va = Va0 + Va1 + Va2
Vb = Vb0 + α 2Va1 + α Va2
Vc = Vc0 + α Va1 + α 2Va2

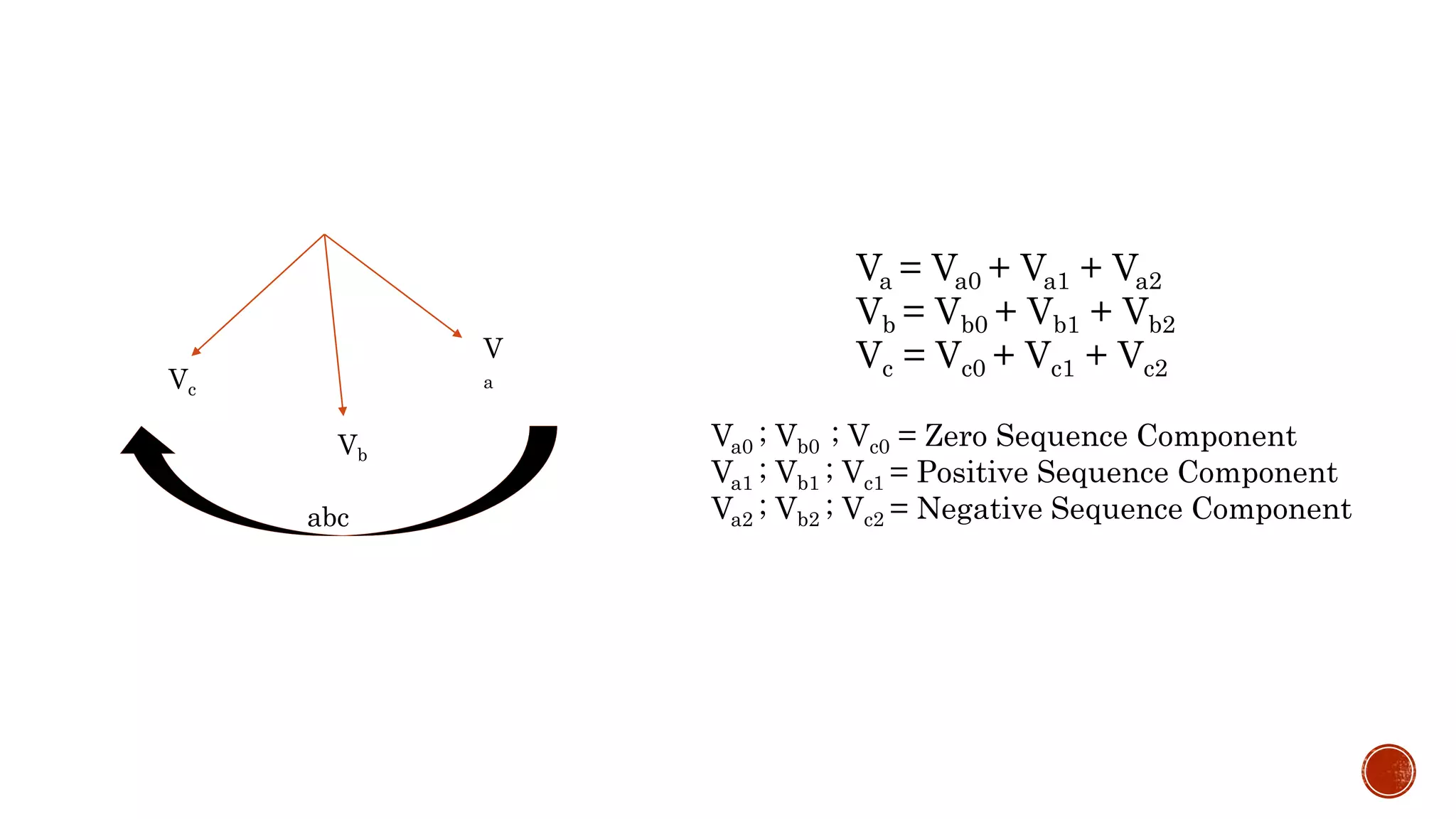
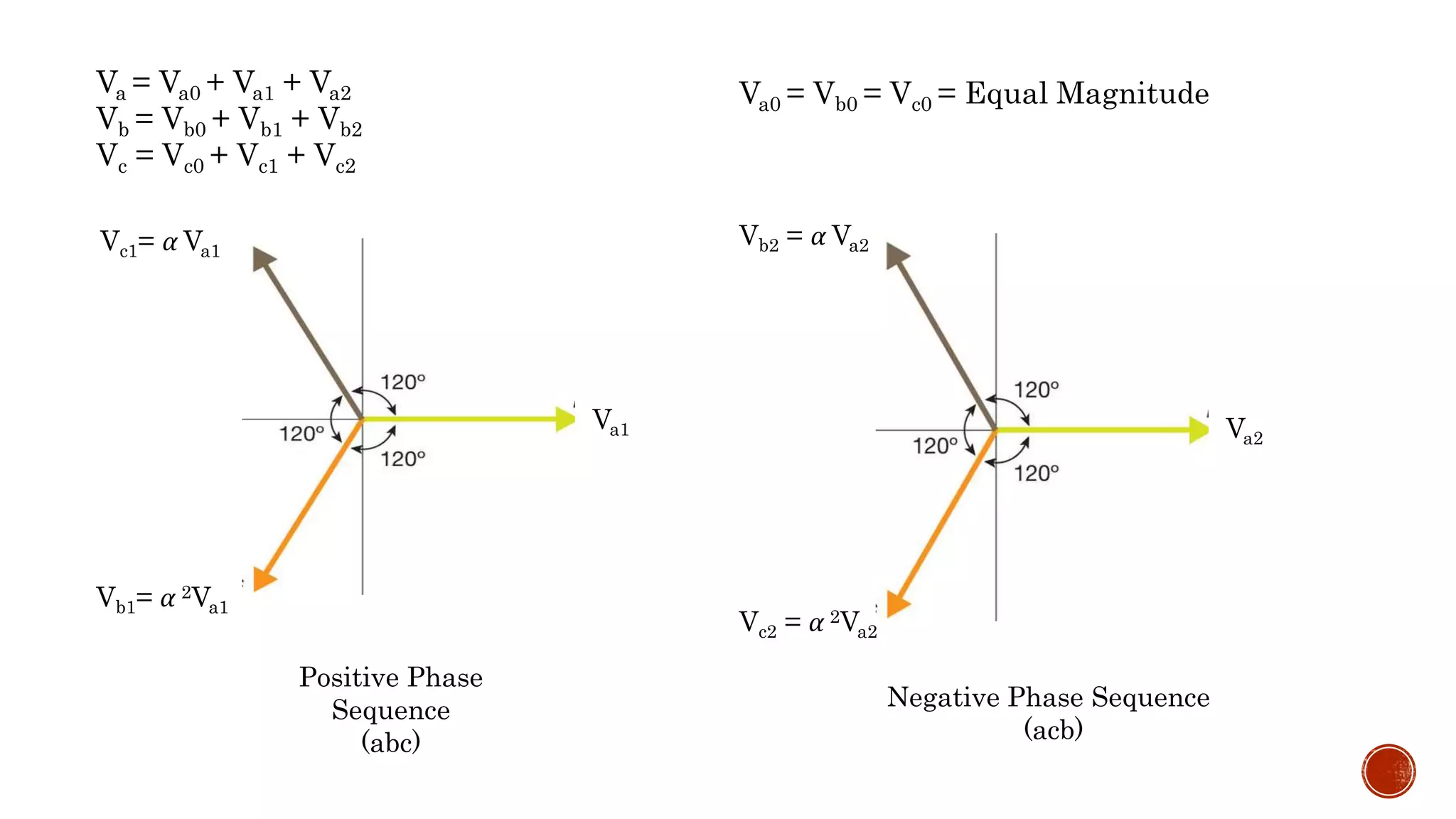
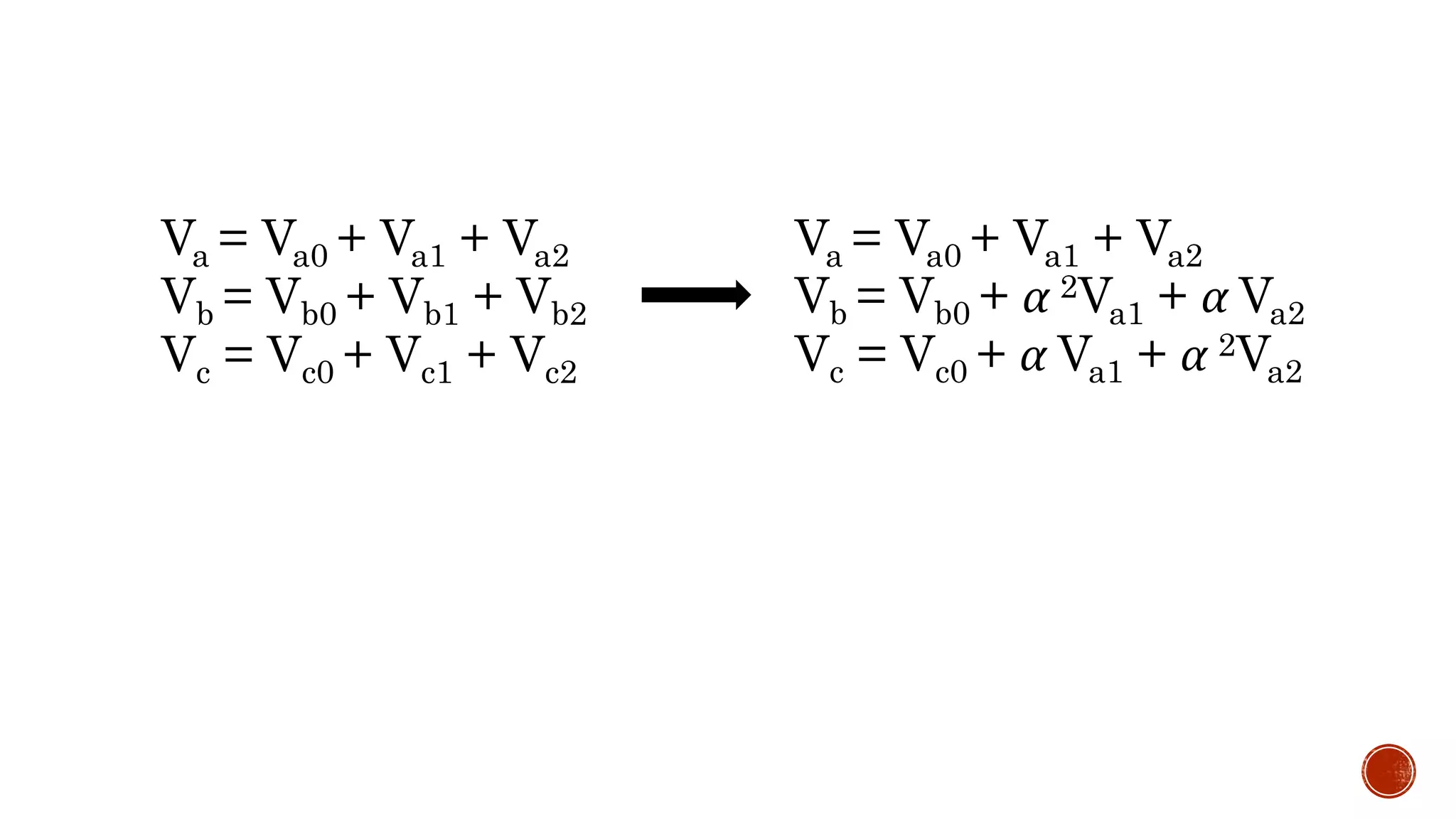
18. Va = Va0 + Va1 + Va2
Vb = Vb0 + α 2Va1 + α Va2
Vc = Vc0 + α Va1 + α 2Va2
Va
Vb
Vc
=
1 1 1
1 𝑎2 𝑎
1 𝑎 𝑎2
𝑉𝑎0
𝑉𝑎1
𝑉𝑎2
[V]=[A][a]
[𝐴−1
][V] = [a]
1 1 1
1 𝑎2 𝑎
1 𝑎 𝑎2
−1
Va
Vb
Vc
=
𝑉𝑎0
𝑉𝑎1
𝑉𝑎2
1 1 1
1 𝑎2 𝑎
1 𝑎 𝑎2
−1
=
1
3
1 1 1
1 𝑎 𝑎2
1 𝑎2 𝑎
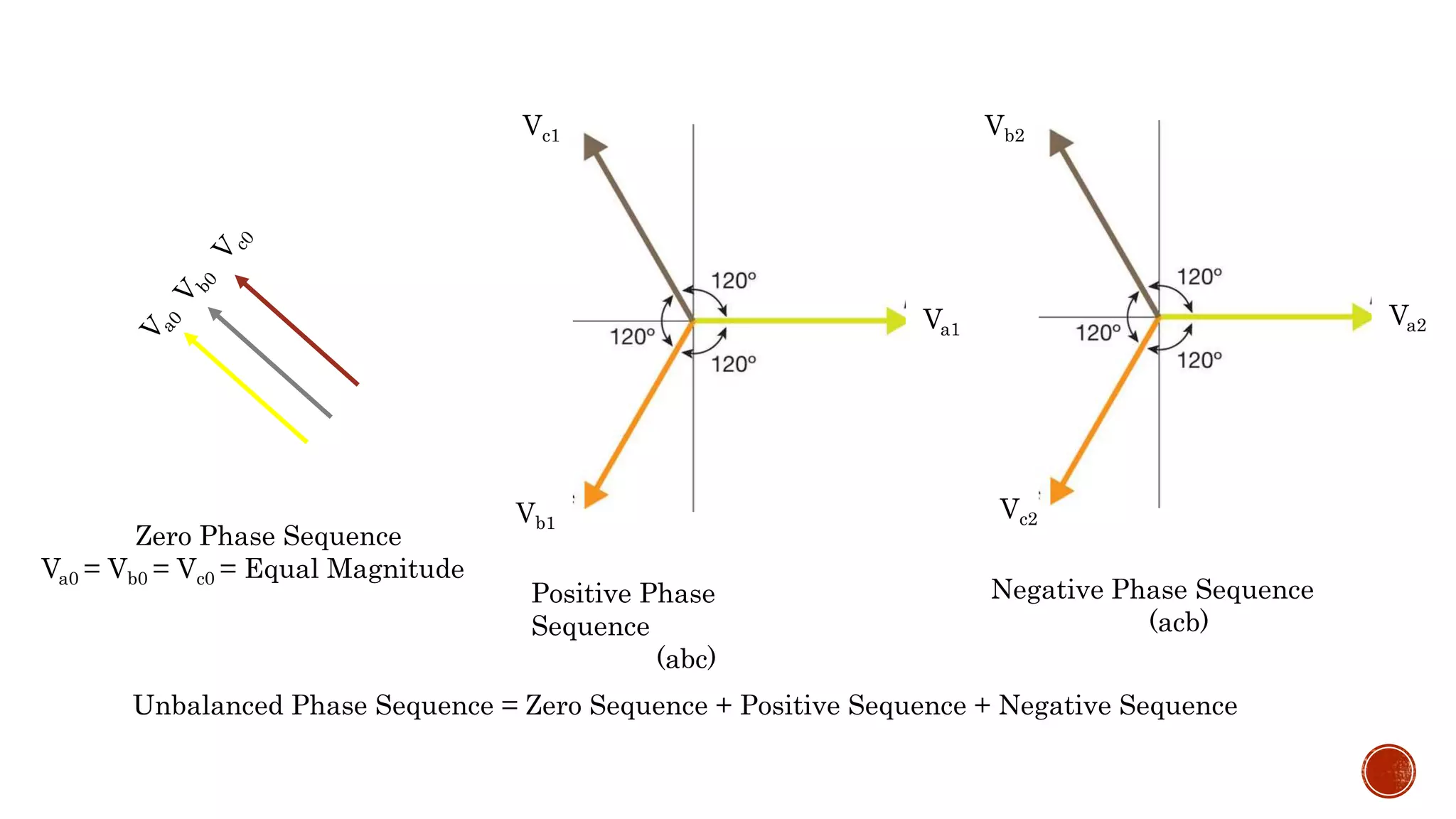
Va0 = Vb0 = Vc0 = Equal Magnitude

19. 𝑉𝑎0
𝑉𝑎1
𝑉𝑎2
=
1
3
1 1 1
1 𝑎 𝑎2
1 𝑎2
𝑎
Va
Vb
Vc
[𝑉𝑎0] =
1
3
[𝑉𝑎 + 𝑉𝑏+ 𝑉𝑐]
[𝑉𝑎2] =
1
3
[𝑉𝑎 + 𝑎2
𝑉𝑏+ 𝑎𝑉𝑐]
[𝑉𝑎1] =
1
3
[𝑉𝑎 + 𝑎𝑉𝑏+𝑎2 𝑉𝑐]

20. References
 Beeman, Donald (1955). "Short-Circuit-Current Calculating Procedures". In Beeman, Donald (ed.). Industrial
Power Systems Handbook. McGraw-Hill. pp. see esp. 38–41, 52–55.
 Elgerd, Olle I. (2007). "§2.5 Per-Unit Representation of Impedances, Currents Voltages and Powers". Electric
Energy Systems Theory: An Introduction (1971 1st ed.). Tata McGraw-Hill. pp. 35–39. ISBN 978-0070192300.
 Yuen, Moon H. (Mar–Apr 1974). "Short Circuit ABC--Learn It in an Hour, Use It Anywhere, Memorize No
Formula". IEEE Trans. on Industry Applications. IA-10 (2): 261–272. doi:10.1109/TIA.1974.349143.
 William D., Jr, Stevenson, (1975). Elements of power system analysis (3rd ed.). New York: McGraw-
Hill. ISBN 0-07-061285-4.
 Weedy, B.M. (1972). Electric power systems (2nd ed.). London ; Toronto: J. Wiley. ISBN 0-471-92445-8.
 Glover, J. Duncan; Sarma, Mulukutla; Overbye, Thomas J. (2011). Power System Analysis and Design. Cengage
Learning. pp. 108–116. ISBN 111142577