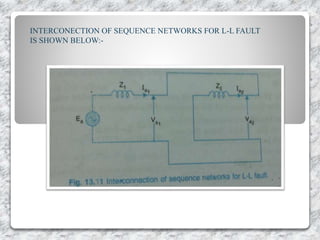
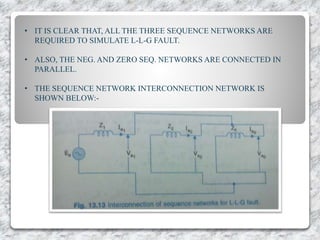
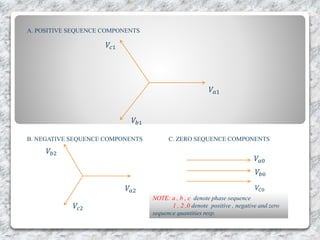
This document provides an overview of symmetrical components for analyzing three-phase power systems. It introduces symmetrical components and how they can be used to simplify fault calculations. The key symmetrical components are defined as the positive, negative, and zero sequence components. Equations are presented to express the original unbalanced phase voltages and currents in terms of these symmetrical components. The significance of each component is described. Methods for calculating faults using symmetrical components are also outlined.

1. ELECTRICAL ENGINEERING DEPARTMENT
SYMMETRICAL COMPONENTS
PRESENTED BY -
-GOPAL KRISHNA MOTI -SURENDRA M. BUTLE
-UDAY DILIPRAO WANKAR - VILAS JAIPAL DORLE
STAFF IN CHARGE -
PROF.AWALE MADAM

2. 𝐼𝑁𝐷𝐸𝑋
1. INTRODUCTION
2. 3-PHASE SYSTEM
3. SIGNIFICANCE OF POSITIVE,NEGATIVEAND ZERO
SEQUENCE COMPONENTS
4. AVERAGE 3-PHAE POWER IN TERMS OF SYMMETRICAL
COMPONENTS
5. SEQUENCE IMPEDANCES
6. FAULT CALCULATION
7. SEQUENCE NETWORK EQUATION
8. SINGLE LINE TO GROUND FAULT
9. SEQUENCE NETWORKS
10. FAULTS ON POWER SYSTEMS
11. REACTORS
12. APPLICATIONS
13. CONCLUSION
14. REFERENCES

3. INTRODUCTION
 IN 1918,DR.C.L.FORTESCUE PRESENTESENTED A PAPER ENTITLED-
METHOD OF SYMMETRICAL CO-ORDINATES APPLIED TO
SOLUTION OF POLYPHASE NETWORKS
AT AIEE.
 HE PROVED THAT, “ A SYSTEM OF n VECTORS OR QUANTITIES MAY BE
RESOLVED, WHEN n IS PRIME, INTO n DIFFERENT SYMETRICAL GROUPS OR
SYSTEMS, ONE OF WHICH CONSISTS OF n EQUAL VECTORS AND THE
REMAINING (n-1) SYSTEM CONSISTS OF n EQUISPACED VECTORS WHICH WITH
FIRST MENTIONED GROUP OF EQUAL VECTORS FORMS AN EQUAL NUMBER
OF SYMMETRICAL n PHASE SYSTEMS.”
 THE METHOD OF SYMMETRICAL COMPNENT IS A GENERAL ONE APPLICABLE
TO ANY POLYPHASE SYSTEM.
 GENERALLY, SYMMETRCAL COMPONENT METHOD IS USED FOR ANALYSIS OF
3-PH SYSTEM AS IT IS MORE FAMILIAR TO ELECRICAL ENGINEERS.

4. 3-PHASE SYSTEM
 ANY THREE COPLANAR VECTORS 𝑉𝑎 ,𝑉𝑏 AND 𝑉𝑐 CAN BE EXPRESSED IN TERMS OF
THREE NEW VECTORS 𝑉1, 𝑉2 AND 𝑉3 BY THREE SILMULTANEOUS LINEAR
EQUATIONS WITH CONSTANT COEFFICIENTS.
 THUS-
𝑉𝑎 = 𝑎11 𝑉1 + 𝑎12 𝑉2 + 𝑎13 𝑉3 --------(1)
𝑉𝑏 = 𝑎21 𝑉1 + 𝑎22 𝑉2 + 𝑎23 𝑉3 ---------(2)
𝑉𝑐 = 𝑎31 𝑉1 + 𝑎32 𝑉2 + 𝑎33 𝑉3 ---------(3)
 EACH OF THE ORIGINAL VECTORS IS REPLACED BY A SET OF THREE VECTORS
MAKING A TOTAL OF NINE VECTORS.
 CONDITIONS:-
1. CALCULATIONS SHOULD BE SIMPLIFIED BY THE USE OF THE CHOSEN
SYSTEM OF COMPONENTS.THIS IS POSSIBLE ONLY IF THE IMPEDANCES(OR
ADMITTANCES)ASSOCIATED WITH THE COMPONENTS OF CURRENT(OR VOLTAGE)
CAN BE OBTAINED READILY BY CALCULATIONS OR TEST.
2. THE SYSTEM OF COMPONENTS CHOSEN SHOULD HAVE PHYSICA SIGNIFICANCE
AND BE AN AID IN DETERMINING POWER SYSTEM PERFORMANCE.

5. FUNDAMENTAL PRINCIPLE
 ACCORDING TO FORTESCUE THEOREM, THE THREE UNBALANCED VECTORS 𝑉𝑎 ,𝑉𝑏
AND 𝑉𝑐 CAN BE REPLACED BY A SET OF THREE BALANCED SYSTEM OF VECTORS.
 A BALANCED SYSTEM OF THREE VECTORS IS ONE IN WHICH THE VECTORS ARE
EQUAL IN MAGNITUDE AND ARE EQUI-SPACED.
 THE THREE SYMMETRICAL COMPONENT VECTORS REPLACING 𝑉𝑎 , 𝑉𝑏 AND 𝑉𝑐 ARE-
• POSITIVE SEQUENCE COMPONENTS :- IT HAS THREE VECTORS OF EQUAL
MAGNITUDE BUT DISPLACED IN PHASE FROM EACH OTHER BY 1200
AND
HAS THE SAME PHASE SEQUENCE AS THE ORIGINAL VECTORS.
• NEGATIVE SEQUENCE COMPONENTS :- IT HAS THREE VECTORS OF EQUAL
MAGNITUDE BUT DISPALCED IN PHASE FROM EACH OTHER BY 1200
AND
HAS THE PHASE SEQUENCE OPPOSITE TO THE ORIGINAL VECTORS.
• ZERO SEQUENCE COMPONENTS :- IT HAS THREE VECTORS OF EQUAL
MAGNITUDE AND ALSO ARE IN PHASE WITH EACH OTHER.

6. A. POSITIVE SEQUENCE COMPONENTS
𝑉𝑎1
𝑉𝑐1
𝑉𝑏1
B. NEGATIVE SEQUENCE COMPONENTS C. ZERO SEQUENCE COMPONENTS
𝑉𝑎2
𝑉𝑏2
𝑉𝑐2
𝑉𝑎0
𝑉𝑏0
𝑉𝐶0
NOTE: a , b , c denote phase sequence
1 , 2 ,0 denote positive , negative and zero
sequence quantities resp.

7. SIGNIFICANCE OF POSITIVE, NEGATIVE AND ZERO SEQUENCE
COMPONENTS
• IF A SET OF POSITIVE SEQUENCE VOLTAGES IS APPLIED TO THE STATOR
WINDING OF THE ALTERNATOR,THE DIRECTION OF ROTATION OF THE
STATOR FIELD IS THE SAME AS THAT OF ROTOR.
• IF A SET OF NEGATIVE SEQUENCE VOLTAGES IS APPLIED TO THE STATOR
WINDING OF THE OF THE ALTERNATOR, THE DIRECTION OF ROTATION
OF STATOR FIELD IS OPPOSITE TO THAT OF ROTOR.
• THE ZERO SEQUENCE VOLTAGES ARE SINGLE PHASE VOLTAGES AND,
THEREFORE THEY GIVE RISE TO AN ALTERNATING FIELD IN SPACE.

8. PHASE VOLTAGES IN TERMS OF THE SYMMETRICAL
COMPONENTS OF PHASE ‘A’
• RELATION BETWEEN ORIGINAL UNBALANCED VECTORS AND THEIR
CORRESPONDING SYMM. COMPONENTS :-
𝑉𝑎 = 𝑉𝑎1 + 𝑉𝑎2 + 𝑉𝑎0 ---------(4)
𝑉𝑏 = 𝑉𝑏1 + 𝑉𝑏2 + 𝑉𝑏0 ---------(5)
𝑉𝑐 = 𝑉𝑐1 + 𝑉𝑐2 + 𝑉𝑐0 ---------(6)
• CONSIDER OPERATOR ʎ WHICH HAS MAGNITUDE UNITY AND ROTATION
THROUGH 1200
.
IMPORTANT RELATIONS:-
ʎ= 1∠1200 = -0.5+j0.866
ʎ2= -1∠1200 =-0.5-j0.866
ʎ3
= 1 ,
ʎ4
= ʎ ,
ʎ2+ʎ+1=0

9. CONT….
RELATION BETWEEN THE SYMMETRICAL COMPONENTS OF PHASE ‘b’AND
‘c’ IN TERMS OF SYMM.COMPONENTS OF PHASE ‘a’
• POSITIVE SEQUENCE VECTORS :-
𝑉𝑎1
𝑉𝑐1
𝑉𝑏1
ʎ
ʎ
𝑉𝑏1 = ʎ2 𝑉𝑎1 ; 𝑉𝑐1 = ʎ𝑉𝑎1
• NEGATIVE SEQUENCE VECTORS:-
𝑉𝑎2
𝑉𝑏2
𝑉𝑐2
ʎ
ʎ
𝑉𝑏2 =ʎ𝑉𝑎1 ; 𝑉𝑐2 = ʎ2 𝑉𝑎2
• ZERO SEQUENCE VECTORS :-
𝑉𝑎0
𝑉𝑏0
𝑉𝑐0
𝑉𝑎0 = 𝑉𝑏0 = 𝑉𝐶0

10. CONT….
SUSTITUTING THE VALUES OF SYMM.COMPONENTS IN EQU.(4),(5) & (6) , WE
GET,
𝑉𝑎 = 𝑉𝑎1 + 𝑉𝑎2 + 𝑉𝑎0 ----------(7)
𝑉𝑏=ʎ2
𝑉𝑎1+ ʎ𝑉𝑎2 + 𝑉𝑎0 ---------(8)
𝑉𝑐= ʎ 𝑉𝑎1+ ʎ2
𝑉𝑎2 + 𝑉𝑎0 -------(9)
SIMILARLLY, RELATION BETWEEN PHASE CURRENTS IN TERMS OF THE
SYMMETRICAL COMPONENTS OF CURRENTS TAKING PHASE ‘a’, IS GIVEN
AS FOLLOWS:-
I 𝑎 = I 𝑎1 + I 𝑎2 + I 𝑎0----------(10)
I 𝑏=ʎ2I 𝑎1+ ʎI 𝑎2 + I 𝑎0---------(11)
I 𝑐= ʎ I 𝑎1+ ʎ2I 𝑎2 + I 𝑎0-------(12)

11. CONT….
TO FIND THE SYMMETRICAL COMPONENTS :-
 TO FIND POSITIVE SEQUENCE COMPONENT 𝑉𝑎1--
MULTIPLY EQU.(7), (8) & (9) BY 1 , ʎ , ʎ2
AND ADDING THEM , WE GET,
 TO FIND NEGATIVE SEQUENCE COMPONENT 𝑉𝑎2--
MULTIPLY EQU.(7), (8) & (9) BY 1 , ʎ2
,ʎ AND ADDING THEM , WE GET
𝑉𝑎2=
1
3
𝑉𝑎 + ʎ2
𝑉𝑏 + ʎ𝑉𝑐 --------(14)
 TO FIND ZERO SEQUENCE COMPONENT 𝑉𝑎0--
ADD EQU.(7), (8) & (9) , WE GET
𝑉𝑎0=
1
3
𝑉𝑎 + 𝑉𝑏 + 𝑉𝑐 --------(15)
𝑉𝑎1=
1
3
𝑉𝑎 + ʎ𝑉𝑏 + ʎ2 𝑉𝑐 --------(13)

12. CONT….
SIMILLARLY SYMMETRICAL COMPONENTS ARE GIVEN AS :--
I 𝑎1=
1
3
I 𝑎 + ʎI 𝑏 + ʎ2
I 𝑐 --------(16)
I 𝑎2=
1
3
I 𝑎 + ʎ2Ib + ʎI 𝑐 --------(17)
I 𝑎0=
1
3
I 𝑎 + I 𝑏 + I 𝑐 --------(18)
AVERAGE 3-PHASE POWER IN TERMS OF SYMMETRICAL
COMPONENTS:-
THE AVERAGE POWER ,
P = 𝑉𝑎 𝐼 𝑎 cos ∅ 𝑎 + 𝑉𝑏 𝐼 𝑏 cos ∅ 𝑏+𝑉𝑐 𝐼𝑐 cos ∅ 𝑐
= 𝑉𝑎. 𝐼 𝑎 +𝑉𝑏. 𝐼 𝑏+𝑉𝑐. 𝐼𝑐
=(𝑉𝑎1 + 𝑉𝑎2 + 𝑉𝑎0).(I 𝑎1 + I 𝑎2 + I 𝑎0) + (ʎ2 𝑉𝑎1+ ʎ𝑉𝑎2 + 𝑉𝑎0).(ʎ2
I 𝑎1+ʎI 𝑎2 + I 𝑎0)
+ (ʎ 𝑉𝑎1+ ʎ2
𝑉𝑎2 + 𝑉𝑎0) .(ʎ I 𝑎1+ ʎ2
I 𝑎2 + I 𝑎0)
TAKE EACH TERM ON RHS ,EXPAND AND REARRANGE THE EQUATION, WE GET,
P = 3[ |𝑉𝑎1| 𝐼 𝑎1 cos 𝜃1 + |𝑉𝑎2| 𝐼 𝑎2 cos 𝜃2 + |𝑉𝑎0| 𝐼 𝑎0 cos 𝜃0]

13. SEQUENCE IMPEDANCES
• THE SEQUENCE IMPEDANCES OF AN EQUIPMENT OR A COMPONENT OF POWER SYSTEM
ARE THE POSITIVE , NEGATIVE AND ZERO SEQUENCE IMPEDANCES.
POSITIVE SEQUENCE IMPEDANCE (𝑍1) :- IT IS THE IMPEDANCE OFFERED BY THE
EQUIPMENT TO THE FLOW OF POSITIVE SEQUENCE CURRENTS.
NEGATIVE SEQUENCE IMPEDANCES(𝑍2) :- IT IS THE IMPEDANCE OFFERED BY THE
EQUIPMENT TO THE FLOW OF NEGATIVE SEQUENCE CURRENTS.
ZERO SEQUENCE IMPEDANCES(𝑍0):- IT IS THE IMPEDANCE OFFERED BY THE
EQUIPMENT TO THE FLOW OF ZERO SEQUENCE CURRENTS.
• FOR 3 PH ,SYMM. STATIC CIRCUIT WTHOUT INTERNAL VOLTAGES LIKE
TRANSFORMER AND TRANSMISION LINE, THE IMPEDANCES TO THE CURRENTS OF
ANY SEQ. ARE THE SAME IN THREE PHASE.
• ALSO CURRENTS OF PARTICULAR SEQUENCE WILL PRODUCE DROP OF THE SAME
SEQUENCE ONLY.
• HOWEVER, FOR STATIC CIRCUIT, POSITIVE AND NEGATIVE SEQUENCE IMPEDANCES
ARE EQUAL. ZERO SEQUENCE IMPEDANCES INCLUDES THE IMPEDANCE PATH
THROUGH GROUND.

14. CONT….
• IN SYMMETRICAL ROTATING MACHINE, THE IMPEDANCE MET BY
ARMATURE CURRENTS OF A GIVEN SEQUENCE ARE EQUAL IN 3-PH.
• BUT BY DEFINITION OF IT WILL DEPEND UPON THE PHASE ORDER OF
THE SEQUENCE CURRENT RELATIVE TO DIRECTION OF ROTATION OF
ROTOR.
• HENCE, IN GENERAL, POSITIVE AND NEGATIVE SEQUENCE IMPEDANCES
ARE UNEQUAL.
• IN FACT, FOR A ROTATING MACHINE, POSITIVE SEQ. IMPEDANCE VARIES,
HAVING MINIUM VALUE IMMEDIATELY FOLLOWING FAULT AND THEN
INCREASES WITH THE TIME UNTILL STEADY STATE CONDITIONS ARE
REACHED WHEN THE POSITIVE SEQUENCE IMPEDANCES CORRESPONDS
TO SYNCHRONOUS IMPEDANCE.
• THUS FOR SYMMETRICAL SYSTEM, THERE IS NO MUTUTAL COUPLING
BETWEEN THE SEQUENCE NETWORKS.

15. FAULT CALCULATIONS
FAULTS CAN BE CLASSIFIED AS :-
1. SHUNT FAULTS (SHORT CIRCUIT)
2. SERIES FAULTS (OPEN CONDUCTOR)
1. SHUNT FAULTS :--
A. IT INVOLVES POWER CONDUCTOR OR CONDUCTORS TO GROUND OR SHORT
CIRCUIT FAULT.
B. SHUNT TYPE OF FAULTS ARE CLASSIFIED AS—
1. LINE TO GROUND FAULT
2. LINE TO LINE FAULT
3. DOUBLE LINE TO GROUND FAULT
4. 3 PH FAULT.
2. SERIES FAULTS :--
A. WHEN CIRCUITS ARE CONTROLLED BY FUSES OR ANY DEVICE WHICH DOES
NOT OPEN ALL THREE PHASES OF THE CIRCUIT MAY BE OPENED WHILE OTHER
PHASES OR PHASE IS CLOSED,THEN CALLED AS SERIES TYPE OF FAULT.
B. SERIES TYPES OF FAULT ARE CLASSIFIED AS:-
1. ONE OPEN CONDUCTOR FAULT.
2. TWO OPEN CONDUCTOR FAULT.

16. VOLTAGE OF THE NEUTRAL :--
• THE VOLTAGE OF THE NEUTRAL WHEN IT S GROUNDED THROUGH
SOME IMPEDANCE OR ISOLATED, WILL NOT BE AT GROUND POTENTIAL
UNDET UNBALANCED CONDITIONS SUCH AS UNSYMMETRICAL FAULTS.
• THE POTENTIAL OF THE NEUTRAL IS GIVEN AS
𝑉𝑛 = −𝐼 𝑛 𝑍 𝑛
WHERE, 𝑍 𝑛= NEUTRAL GROUNDING IMPEDANCE.
NEGATIVE SIGN DENOTES CURENT FLOW FROM THE GROUND TO
NEUTRAL OF THE SYSTEM.
• FOR 3 PHASE SYSTEM,
𝐼 𝑛= 𝐼 𝑎 + 𝐼 𝑏 + 𝐼𝑐
= (I 𝑎1 + I 𝑎2 + I 𝑎0)+(ʎ2I 𝑎1+ ʎI 𝑎2 + I 𝑎0)+(ʎ I 𝑎1+ ʎ2I 𝑎2 + I 𝑎0)
= 3 𝐼0
THEREFORE,
𝑉𝑛= −3𝐼 𝑎0 𝑍 𝑛
SINCE THE POSITIVE AND NEGATIVE SEQUENCE COMPONENTS ARE
ABSENT THROUGH NEUTRAL.

17. SEQUENCE NETWORK EQUATIONS
• THESE EQU. ARE DERIVED FOR AN UNLOADED ALTERNATOR WITH NEUTRAL
SOLIDLY GROUNDED, ASSUMING BALANCED SYSTEM.

18. 1.POSITIVE SEQUENCE VOLTAGE IS GIVEN BY–
𝑉𝑎1 = 𝐸 𝑎 − 𝐼 𝑎1 𝑍1
2.NEGATIVE SEQUENCE VOLTAGE IS GIVEN BY-
𝑉𝑎2 = 𝐸 𝑎2 − 𝐼 𝑎2 𝑍2
= 0 - 𝐼 𝑎2 𝑍2
𝑉𝑎2=−𝐼 𝑎2 𝑍2
3.ZERO SEQUENCE VOLTAGES IS GIVEN BY –
𝑉𝑎0 = 𝑉𝑛 − 𝐼 𝑎0 𝑍 𝑔0
=−3𝐼 𝑎0 𝑍 𝑛 − 𝐼 𝑎0 𝑍 𝑔0
= −𝐼 𝑎0(𝑍 𝑔0+3𝑍 𝑛)
𝑉𝑎0 = −𝐼 𝑎0 𝑍0
where, 𝑍 𝑔0 = 𝑍𝐸𝑅0 𝑆𝐸𝑄. 𝐼𝑀𝑃𝐸𝐷𝐴𝑁𝐶𝐸 𝑂𝐹 𝐺𝐸𝑁.
𝑍 𝑛 = 𝑁𝐸𝑈𝑇𝑅𝐴𝐿 𝐼𝑀𝑃𝐸𝐷𝐴𝑁𝐶𝐸

19. CONT….
THUS CORRSONDING SEQUENCE NETWORKS FOR THE ULOADED
ALTERNATOR ARE SHOWN BELOW ;

20. SINGLE LINE TO GROUND FAULT
1.LET THE FAULT TAKES PLACE ON PHASE A.
2. THE BOUNDARY CONDITIONS ARE-
𝑉𝑎 = 0 , 𝐼 𝑏 = 0, 𝐼𝑐 = 0

21. THE SEQUENCE NETWORK EQUATIONS ARE :-
𝑉𝑎1 = 𝐸 𝑎 − 𝐼 𝑎1 𝑍1
𝑉𝑎2=−𝐼 𝑎2 𝑍2
𝑉𝑎0 = −𝐼 𝑎0 𝑍0
THE SOLUTION FOR THESE EQUATION WILL GIVE SIX UNKNOWNS 𝑉𝑎1
, 𝑉𝑎2, 𝑉𝑎0 AND 𝐼 𝑎1 ,𝐼 𝑎2 AND 𝐼 𝑎0.
WE HAVE,
I 𝑎1=
1
3
I 𝑎 + ʎI 𝑏 + ʎ2
I 𝑐
I 𝑎2=
1
3
I 𝑎 + ʎ2
Ib + ʎI 𝑐
I 𝑎0=
1
3
I 𝑎 + I 𝑏 + I 𝑐
SUBSTITUTING THE VALUES OF 𝐼 𝑏 AND 𝐼𝑐 IN ABOVE EQUATIONS WE GET,
𝐼 𝑎1=𝐼 𝑎2= 𝐼 𝑎0.= 𝐼 𝑎/3
CONT….

22. NOW, SUBSTITUTUING THE VALUES OF 𝑉𝑎1 , 𝑉𝑎2,𝑉𝑎0FROM THE
SEQUENCE NETWORK EQUATION, WE GET,
THE EQUATION 𝑉𝑎 = 0 CAN BE WRITTEN IN TERMS OF SYMMETRICAL
COMPONENTS ,
𝑉𝑎 = 0 = 𝑉𝑎1 + 𝑉𝑎2 + 𝑉𝑎0
𝐸 𝑎 − 𝐼 𝑎1 𝑍1 − 𝐼 𝑎2 𝑍2 − 𝐼 𝑎0 𝑍0=0
SINCE,
𝐼 𝑎1 =𝐼 𝑎2 = 𝐼 𝑎0
WE GET,
𝐸 𝑎 − 𝐼 𝑎1 𝑍1 − 𝐼 𝑎1 𝑍2 − 𝐼 𝑎1 𝑍0=0
𝐼 𝑎1 =
𝐸 𝑎
𝑍1 + 𝑍2 + 𝑍0
CONT….

23. IT IS CLEAR THAT, TO SIMULATE A L-G FAULT ALL THE SEQUENCE
NETWORKS ARE REQUIRED AND SINCE THE CURRENTS ARE ALL EQUAL IN
MAGNITUDE AND PHASE ANGLE, THEREFORE,THE THREE SEQUENCE
NETWORKS MUST BE CONNECTED IN SERIES.
CONT….

24. IN CASE OF LINE TO GROUND FAULT,
𝐼 𝑛 = 3𝐼 𝑎0
IF THE NEUTRAL IS NOT GROUNDED THE ZERO SEQUENCE IMPEDANCE
𝑍0 ,BECOMES INFINITE. THEREFORE,
𝐼 𝑎1 =
𝐸 𝑎
𝑍1 + 𝑍2 + ∞
= 0
HENCE, 𝐼 𝑎1 =𝐼 𝑎2 = 𝐼 𝑎0=0
THIS MEANS THAT,FOR THIS SYSTEM,THE FAULT CURRENT 𝐼 𝑎=0

25. LINE TO LINE FAULT
1.THE LINE TO LINE-LINE FAULT TAKES PLACE ON PHASE B AND C .
2. THE BOUNDARY CONDITIONS ARE :-
𝐼 𝑎=0
𝐼 𝑎 + 𝐼 𝑏 = 0
𝑉𝑏 = 𝑉𝑐

26. FOR LINE-LINE FAULT,THE ZERO SEQUENCE COMPONENT OF CURRENT IS
ABSENT AND POSITIVE SEQUENCE COMPONENT OF CURRENT IS EQUAL IN
MAGNITUDE BUT OPPOSITE IN PHASE TO NEGATIVE SEQUENCE
COMPONENT OF CURRENT, I.E.
𝐼 𝑎1 = − 𝐼 𝑎2
IN LINE-LINE FAULT, ZERO SEQUENCE COMPONENT OF CURRENT IS ABSENT.
𝐼 𝑎0=0
ALSO,
POSITIVE SEQUENCE COMPONENT OF VOLTAGE EQUALS THE NEGATIVE
SEQUENCE COMPONENT OF VOLTAGE.THEREFORE THE SEQUENCE NETWORK
ARE CONNECTED IN PARALLEL.
𝑉𝑎1 = 𝑉𝑎2
𝐸 𝑎 − 𝐼 𝑎1 𝑍1=-𝐼 𝑎2 𝑍1 = 𝐼 𝑎1 𝑍1
𝐼 𝑎1=
𝐸 𝑎
𝑍1+𝑍2

27. INTERCONECTION OF SEQUENCE NETWORKS FOR L-L FAULT
IS SHOWN BELOW:-

28. DOUBLE LINE TO GROUND FAULT
1.DOUBLE LINE TO GROUND FAULT TAKES PLACE ON PHASE B AND C.
2.THE BOUNDARY CONDITIONS ARE—
𝐼 𝑎=0,𝑉𝑏 =0,𝑉𝐶 = 0
3. THE SEQUENCE NETWORK IS SHOWN BELOW:-

29. IN L-L-G FAULT, POSITIVE SEQUENCE,NEGATIVE SEQUENCE AND
ZERO SEQUENCE VOLTAGES ARE SAME.
𝑉𝑎1 = 𝑉𝑎2=𝑉𝑎3
ALSO,
I 𝑎 = I 𝑎1 + I 𝑎2 + I 𝑎0 = 0
SUBSTITUTING VALUES OF I 𝑎2 AND I 𝑎0 FROM EQU.
I 𝑎1 −
𝐸 𝑎 − 𝐼 𝑎1 𝑍1
𝑍2
−
𝐸 𝑎 − 𝐼 𝑎1 𝑍0
𝑍0
= 0
REARRANGING THE TERMS,WE GET,
I 𝑎1 =
𝐸 𝑎
𝑍1 +
𝑍0 𝑍2
𝑍0 + 𝑍2

30. • IT IS CLEAR THAT, ALL THE THREE SEQUENCE NETWORKS ARE
REQUIRED TO SIMULATE L-L-G FAULT.
• ALSO, THE NEG. AND ZERO SEQ. NETWORKS ARE CONNECTED IN
PARALLEL.
• THE SEQUENCE NETWORK INTERCONNECTION NETWORK IS
SHOWN BELOW:-

31. 3-PHASE FAULT
1. THE BOUNDARY CONDITIONS ARE--
𝐼 𝑎 + 𝐼 𝑏 + 𝐼𝑐 = 0
𝑉𝑎 = 𝑉𝑏=𝑉𝐶
2. CIRCUIT DIAGRAM:-

32. 3.SINCE,
| I 𝑎|= |I 𝑏| = |I 𝑐|
4.TAKE I 𝑎 AS REFERRENCE. WE GET
𝐼 𝑏 = ʎ2
𝐼 𝑎AND 𝐼 𝐶 = ʎ𝐼 𝑎
5. USING THE RELATION,
I 𝑎1=
1
3
I 𝑎 + ʎI 𝑏 + ʎ2I 𝑐
I 𝑎2=
1
3
I 𝑎 + ʎ2
Ib + ʎI 𝑐
I 𝑎0=
1
3
I 𝑎 + I 𝑏 + I 𝑐
6. WE GET,
I 𝑎1=I 𝑎 , I 𝑎2=0 AND I 𝑎0=0
7. IN THIS SYSTEM, ZERO AND NEG.SEQ.COMPONENT OF CURRENT
ARE ABSENT.
8. THE POSITIVE SEQUENCE COMPONENT OF CURRENT IS EQUAL
TO PHASE CURRENT.
9. SIMILLARY,
𝑉𝑎1 = 𝑉𝑎2 = 𝑉𝑎0 = 0

33. • FROM THE ANALYSIS OF THE VARIOUS FAULTS,THE OBSERVATIONS ARE
MADE.
1. THE POSITIVE SEQUENCE CURRENTS ARE PRESENT ON ALL TYPES OF
FAULT.
2. NEGATIVE SEQUENCE CURRENTS ARE PRESENT IN ALL
UNSYMMETRICAL FAULTS.
3. ZERO SEQUENCE CURRENTS ARE PRESENT WHEN THE NEUTRAL OF THE
SYSTEM IS GROUNDED AND THE FAULT ALSO INVOLVES THE GROUND,
AND MAGNITUDE OF THE NEUTRAL CURRENT IS EQUAL TO 3𝐼 𝑎0.

34. SEQUENCE NETWORK
1. THE ZERO SEQUENCE NETWORK IS SIMILAR TO POSITIVE SEQUENCE
NETWORK EXCEPT FOR THE FACT THAT SINCE NO NEGATIVE SEQUENCE
VOLTAGES ARE GENENRATED,THE SOURCE OF EMF IS ABSENT.
2. THE GENERAL CIRCUIT :-

35. • THERE ARE TWO SERIES AND SHUNT SWITCHES.
• ONE SERIES AND ONE SHUNT SWITCH ARE FOR BOTH THE SIDES
SEPARATELY.
• THE SERIES SWITCH OF PARTICULAR SIDE IS CLOSED IF IT IS STAR
GROUNDED AND THE SHUNT SWITCH IS CLOSED IF THAT SIDE IS
DELTA CONNECTED,OTHERWISE OPEN.