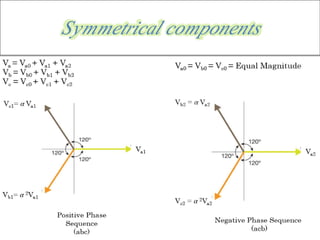
This document discusses symmetrical components and their application to analyzing unbalanced three-phase systems. It introduces symmetrical components as a method to represent an unbalanced system using balanced components. Specifically, it describes: 1. Representing an unbalanced three-phase system using positive, negative, and zero sequence components, which transforms the system into balanced phasors that rotate in different directions. 2. Calculating symmetrical components of voltage and current by applying transformation matrices to the phase quantities. 3. Relating line and phase quantities of voltage and current using symmetrical components. Line quantities are determined from the phase quantities. 4. Expressing complex power in an unbalanced system using symmetrical components, allowing power calculations to be

1. Lec3:Symmetrical components
Prepared by :
Eng/Zaki Mohammed Al Shadaddi

2. Symmetrical components
Type of fault:
- Symmetrical fault - unsymmetrical fault
(L-L-L) (L-L,L-L-G,L-G)
(value of V&I will change and value of V&I will
change
remain in balance condition)
• For balance system and symmetrical component , if we want to
find the electrical quantities (V&I) of system ,
we will use per phase model of system
• For unbalance system we cant use per phase model of system ,
we will write equation for each phase which will take more time ,
so we will use symmetrical components

3. Symmetrical components
set of vector / component
Unbalanced ͢͢ balance condition
N phase = (n-1)set of n-phase + one set of n phase For
unbalanced system balance phasor with
different rotation
Ex :3Ф,3wire/4wire
Phase = 2 set of 3-phase + one set of cophasial phasor -3
Unbalance condition balance phasor
↓ ↓
- positive sequence zero sequence
component
- negative sequence
component

4. Symmetrical components
 3-phase unbalance system(a ,b ,c )
represented
Positive sequence 1
Negative sequence 2
Zero sequence 0

6. Symmetrical components
As a 3-phase unbalance condition
3 voltage variable
3 current variable
Due to this there will be 9 variable , so we will use operator a
which reduce the variable from 9 to 3

7. Symmetrical components

8. Symmetrical components

9. Symmetrical components
Unbalance voltage and current in term of symmetrical components

10. Symmetrical components
Unbalance voltage and current in term of symmetrical components

11. Symmetrical components

12. Symmetrical components

13. Symmetrical components
(i) 𝐼120 = [𝐴]−1[𝐼 𝑎𝑏𝑐 ]
𝐼 𝑎1
𝐼 𝑎2
𝐼 𝑎0
=
1
3
1 𝛼 𝛼2
1 𝛼2 𝛼
1 1 1
𝐼 𝑎
𝐼 𝑏
𝐼 𝑐
𝐼 𝑎1=
1
3
(𝐼 𝑎+ 𝛼 𝐼 𝑏+𝛼2 𝐼𝑐)=
1
3
(100∟30 +1 ∟120*50∟300 +1 ∟240*30∟180)=
57.98 ∟43.3 A
𝐼 𝑎2=
1
3
(𝐼 𝑎+ 𝛼2 𝐼 𝑏+𝛼𝐼𝑐 ) =
1
3
(100∟30 + 1 ∟240*50∟300 + 1 ∟120*30∟180 ) =
18.97 ∟24.96 A
𝐼 𝑎0=
1
3
(𝐼 𝑎+ 𝐼 𝑏+𝐼𝑐) =
1
3
(100∟30 +50∟300 +30∟180 ) =27.29 ∟4.69 A

14. • (ii) current in neutral circuit :-
𝐼 𝑛=𝐼 𝑎+ 𝐼 𝑏+𝐼𝑐
= 𝐼 𝑎1+𝐼 𝑎2 +𝐼 𝑎0
+ 𝐼 𝑏1+ 𝐼 𝑏2 + 𝐼 𝑏0
+ 𝐼𝑐1+ 𝐼𝑐2 + 𝐼𝑐0
= 𝐼 𝑎0 + 𝐼 𝑏0 + 𝐼𝑐0 = 3 𝐼 𝑎0 = 3*27.29 ∟4.69 A =
81.877 ∟4.69A

15. Symmetrical components
• Relationship between line and phase voltage of sequence
components :-

16. Symmetrical components

17. Symmetrical components
= − = − 𝛼 =(1−𝛼) =
3 ∟-30
= − =0
 Conculation :-
1) +ve line voltage ( ) = 3 times of +ve phase voltage
( ) and lead by 30 degree .
2) −ve line voltage ( ) = 3 times of -ve phase voltage
( ) and lag by 30 degree .
3) No zero sequence component exist for line voltage .

18. Symmetrical components
 Relationship between line and phase current(delta) of symmetrical
component:
• For balance condition I= 3 𝐼𝑝ℎ ∠ − 30
• Line current lag phase current by 30(deg)
• Abnormal Condition
• Line current
• Ia= 𝐼𝑎1 + 𝐼𝑎2 + 𝐼𝑎0
• Ib= 𝐼𝑏1 + 𝐼𝑏2 + 𝐼𝑏0
• Ic= 𝐼𝑐1 + 𝐼𝑐2 + 𝐼𝑐0

19. Symmetrical components

20. Symmetrical components

21. Symmetrical components
Conculation:for eq(1)
+ve sequence:-
Line current (Ia1)=√3 time of +ve phase current (Iab1)
and lag by30
-ve sequence:- (Ia2)=√3 time of –ve phase current (Iab2)and
lead by 30
No zero sequence component in the line current

22. Symmetrical components

23. Symmetrical components

24. Symmetrical components

25. Symmetrical components

26. Symmetrical components

27. Symmetrical components

28. Symmetrical components

29. Symmetrical components
• 1-symmetrical/sequence component of line current?
• 2-symmetrical/sequence component of phase current?
• 3- if the value of R=10 then find the unbalanced phase/line
voltage?
• 4-symmetrical component of line /phase voltage ?

30. Symmetrical components

31. Symmetrical components

32. Symmetrical components
Iab=Iab1+Iab2+Iab0=8.3299∠-6.9 A
Ibc=aᶺ2Iab1+aIab2+Iab0=10.542∠138.41 A
Ica=aIab1+𝑎ᶺ2Iab2+Iab0= 6.0092∠-93.66 A
 Step4 :- unbalance phase voltage
Vab= Iab ∗ Zab =83.299∠-6.9 v
vbc= Ibc*Zbc =105.42∠138.41 v
Vca= Ica ∗ Zca=60.098∠-93.66 v
 Step5 :- sequence component of phase /line voltage
Step5 :-sequence(symmetrical)component of phase /line voltage :-
𝑉𝑎𝑏1
𝑉𝑎𝑏2
𝑉𝑎𝑏0
=1/3
1 𝑎 𝑎ᶺ2
1 𝑎ᶺ2 𝑎
1 1 1
𝑉𝑎𝑏
𝑉𝑏𝑐
𝑉𝑐𝑎
𝑉𝑎𝑏1=1/3[𝑉𝑎𝑏+a𝑉𝑏𝑐+𝑎ᶺ2𝑉𝑏𝑐]=26.931 ∠-81.8 v
𝑉𝑎𝑏2=1/3[𝑉𝑎𝑏+𝑎ᶺ2𝑉𝑏𝑐+𝑎𝑉𝑐 𝑎]=80.597 ∠11.922 v
𝑉𝑎𝑏0=1/3[𝑉𝑎𝑏 + 𝑉𝑏𝑐+𝑉𝑐 𝑎]=4.709*10^3 ∠-12.49 v

33. Symmetrical components
 Expression of complex power in term of symmetrical
component :-
Suppose 3 phase system :
S=P+jQ = V 𝐼∗
𝑆3𝑝ℎ = 3 𝑉𝑝ℎ 𝐼∗
𝑝ℎ for balanced condition
= 3𝑉𝐿 𝐼∗
𝐿
 For unbalance condition :-
𝑆3𝑝ℎ = 𝑉𝑎 𝐼 𝑎
∗
+ 𝑉𝑏 𝐼 𝑏
∗
+ 𝑉𝑐 𝐼𝑐
∗
= [ 𝑉𝑎 𝑉𝑏 𝑉𝑐 ]
𝐼 𝑎
∗
𝐼 𝑏
∗
𝐼𝑐
∗
=
𝑉𝑎
𝑉𝑏
𝑉𝑐
𝑇
𝐼 𝑎
∗
𝐼 𝑏
∗
𝐼𝑐
∗
= [ 𝑉𝑎 𝑏𝑐] 𝑇
[ 𝐼 𝑎 𝑏𝑐]∗

34. Symmetrical components

35. Symmetrical components
 Ex :- star configuration with line voltage
=100∟0 v , =80.8 ∟-121.44 v , =90∟130 v
=10Ώ find the power exponded in the resistance
Sol :- method (1):- 𝑆3𝑝ℎ = 𝑉𝑎 𝐼 𝑎
∗
+ 𝑉𝑏 𝐼 𝑏
∗
+ 𝑉𝑐 𝐼𝑐
∗
For last example as we found , ,
𝑆3𝑝ℎ= P + j Q = P+j0 as a resistance load
𝑆3𝑝ℎ= 327.664+275.41504+212.3366 =815.59 w
 method (2):- 𝑆3𝑝ℎ = 3*[ 𝑉𝑎1 𝐼 𝑎1
∗
+ 𝑉𝑎2 𝐼 𝑎2
∗
+ 𝑉𝑎0 𝐼 𝑎0
∗
]=815.59w
 method (3) :- P= 𝑃𝑎+ 𝑃𝑏+ 𝑃𝑐=
𝑉𝑎𝑛
2
𝑅 𝑎
+
𝑉 𝑏𝑛
2
𝑅 𝑏
+
𝑉𝑐𝑛
2
𝑅 𝑐
 method (4):-𝑃3𝑝ℎ = 𝐼 𝑎
2
𝑅 𝑎 + 𝐼 𝑏
2
𝑅 𝑏 + 𝐼𝑐
2
𝑅 𝑐

36. Symmetrical components 26
 Ex :- = 0.9 pu, = -0.2 pu, = -0.1 pu
Base voltage is 11 kv (L.L) , find 1) in pu and kv
2) L.L in pu and kv
Sol :-
= + + = 0.9 – 0.2 – 0.1 = 0.6 pu
= * = 0.6 *
11
3
= 3.811 kv
= - = - - - = - 𝛼2
- 𝛼 -
= 0.6 - 1 ∟240 *0.9 +1 ∟120*0.2 + 0.1
= 0.6 – 1.054 ∟-115.28 = 1.418 ∟42.226 pu
= - = ( -
=1.418 ∟42.226 *
11
3
= 9.0062 kv ∟42.23

37. Symmetrical components
• Sequence impedance of transmission line
By kvl at node a:
𝑉𝑎 − 𝑉𝑎′= 𝐼 𝑎* 𝑍 𝑠 + 𝐼 𝑛 * 𝑍 𝑛 + 𝐼 𝑏* 𝑍 𝑚+ 𝐼𝑐* 𝑍 𝑚
= 𝐼 𝑎[ 𝑍 𝑛+ 𝑍 𝑠]+ 𝐼 𝑏[ 𝑍 𝑚+ 𝑍 𝑛]+ 𝐼𝑐[ 𝑍 𝑚+ 𝑍 𝑛]→(1)
By kvl at node b:
𝑉𝑏 − 𝑉𝑏′= 𝐼 𝑏* 𝑍 𝑠 + 𝐼 𝑛* 𝑍 𝑛+ 𝐼 𝑎* 𝑍 𝑚+ 𝐼𝑐* 𝑍 𝑚
= 𝐼 𝑎[ 𝑍 𝑚+ 𝑍 𝑛]+ 𝐼 𝑏[ 𝑍 𝑚 + 𝑍 𝑠]+ 𝐼 𝐶 [ 𝑍 𝑚+ 𝑍 𝑛]→(2)

38. Symmetrical components

39. Symmetrical components

40. Symmetrical components

41. Symmetrical components

42. Symmetrical components

43. Symmetrical components

44. Symmetrical components

45. Symmetrical components