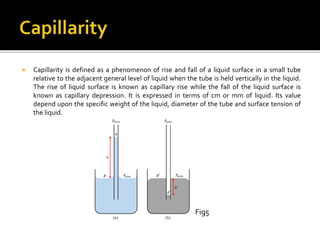
The document discusses surface tension, which is the tensile force acting on a liquid's surface that causes it to behave like a membrane. It outlines the historical contributions of Agnes Pockels to the field, explains phenomena such as capillary rise and fall in small tubes, and describes the balance of forces around liquid droplets and jets. Illustrative figures and equations are included to support the explanations of these concepts.

1. • SurfaceTension
•SurfaceTension in Detail
•SurfaceTension on Liquid Droplet
•SurfaceTension on Hollow Bubble
•SurfaceTension on Liquid Jet
•Capillary
•Expression for Capillary Rise
•Expression for Capillary Fall
•Sources

2.  In 1891, with help of Lord Rayleigh, Agnes Pockels published first paper on Surface Tensionon her
measurements in journal Nature. Thus began her career studying surface films. he never received a
formal appointment, but she published a number of papers and eventually received recognition as a
pioneer in the new field of surface science.
 Surface tension is defined as the tensile force acting on the surface of a liquid in contact with a gas or on
the surface between two immiscible liquids such that the contact surfaces behaves like a membrane
under tension. The magnitude of this force per unit length of the free surface will have the same value as
the surface energy per unit area. It is denoted Greek letter σ (called sigma). In MKS units, it is expressed
as kgf/m while in SI units as N/m.
Fig1

3.  The phenomenon of surface tension is explained by Fig2. Consider three molecules A,B, C of a liquid in a
mass of liquid. The molecule A is attracted in all direction as it submerged and equally surrounded by all
molecules of the liquid. Thus we can say that resultant of forces acting on molecule A is zero. But for
molecule B, which not submerged completely in to the surrounding and situated near to free surface, is
tended to act upward and downward due to forces which are unbalanced. Thus, net resultant force on
molecule B is acting in downwards direction. The molecule C, situated on the free surface of liquid (half
submerged) will experience a resultant force downwards.
 All the molecules on the free surface experience a downward force. Thus the free surface of the liquid
acts like a very thin film under tension of the surface of the liquid act as though it is a elastic membrane
under tension.
Fig2

4.  Consider a small spherical of a liquid of radius ‘r’. On the entire surface of
the droplet, the tensile force due to surface tension will be acting.
 Let σ = Surface tension of the liquid
 p = Pressure intensity inside the droplet (in excess of the outside pressure identity)
 d = Dia. of droplet
Fig3

5.  Imagine the droplet is cut in two halves.The forces acting on left side will be (a) tensile force due to
surface around acting around the circumference of the cut portion as shown in Fig3and this will be equal
to following equation:-
 = σ x circumference (σ x π d)
 (b) pressure force on the area as shown in Fig3 (c).These two forces will be equal and
opposite under equilibrium conditions, that is,
 Above equation shows that with the decrease of diameter of the droplet, pressure intensity inside the
droplet increases.

6.  A hollow bubble like a soap bubble in air has two surfaces in
contact with air, one inside and other outside. Thus two
surfaces are subjected to surface tension. In such case we
have

7.  Consider a liquid jet of diameter ‘d’ and length ‘L’.
Let
 p = Pressure intensity the liquid jet above the outside pressure
 σ = Surface tension of the liquid
 Consider the equilibrium of the semi jet, we have
Force due to pressure = p x area of semi jet
= p x L x d
Force due to surface tension = σ x2L
Equating the forces, we have
p x L x d = σ x 2L
p = (σ x 2L)/(L x d)
Fig4

8.  Capillarity is defined as a phenomenon of rise and fall of a liquid surface in a small tube
relative to the adjacent general level of liquid when the tube is held vertically in the liquid.
The rise of liquid surface is known as capillary rise while the fall of the liquid surface is
known as capillary depression. It is expressed in terms of cm or mm of liquid. Its value
depend upon the specific weight of the liquid, diameter of the tube and surface tension of
the liquid.
Fig5

9.  Consider a glass tube of small diameter ‘d’ opened at both ends and is inserted in a liquid for examples
lets consider liquid as water.The water will rise in the tube above the level of the liquid.
Let h = height of the liquid in the tube. Under a state of equilibrium, the weight of liquid of height
‘h’ is balanced by the force at the surface of the liquid in the tube. But the force at the surface of the
liquid in the tube is due to surface tension.
Let σ = Surface tension of liquid
Θ =Angle of contact between liquid and glass tube.
The weight of liquid of height ‘h’ in the tube = (Area of tube x h) x ρ x g
Where ρ = Density of liquid
Vertical component of the surface tensile force = (σ*Circumference)xcos Θ
= σ* π*d*cosΘ
Fig6

10.  For equilibrium state, equating above to final equations, we get
 The value of Θ between water and clean glass tube is approximately equal to zero and hence cos Θ is
equal to unity.Then rise of water is given by

11.  If the glass tube is dipped in mercury, the level of mercury in the tube will be lower than the
general level of the outside liquid as shown in Fig7
Let h = Height of depression in tube
Then in equilibrium, two forces are acting on the mercury inside the tube. First one is due
to surface tension acting in the downward direction and is equal to σ* π*d*cos Θ. Second
force is due to hydrostatic force acting upward and is equal to intensity of pressure at a
depth ‘h’ x Area
Equating the two, we get
Value of Θ for mercury and glass tube is 128 degrees.
Fig7

12.  Fig1https://en.wikipedia.org/wiki/Agnes_Pockels#/media/File:Agnes_Pockels.jpg
 Fig2 – From Fluid Mechanics and Hydraulics Machines by Dr. R.KBansal
 Fig3 - From Fluid Mechanics and Hydraulics Machines by Dr. R.KBansal
 Fig4 - From Fluid Mechanics and Hydraulics Machines by Dr. R.KBansal
 Fig5 - https://physics.stackexchange.com/questions/517222/pressure-variation-in-a-capillary-tube
 Fig6 - From Fluid Mechanics and Hydraulics Machines by Dr. R.Kbansal
 Fig7 - From Fluid Mechanics and Hydraulics Machines by Dr. R.KBansal
 Book referred for content - From Fluid Mechanics and Hydraulics Machines by Dr. R.Kbansal

13.  Please feel free to comment your suggestion
and any correction.....