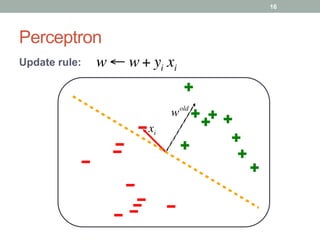
The document discusses the supervised prediction of graph summaries, focusing on various machine learning techniques such as binary classification, ranking, and structured output prediction. It highlights methods like the perceptron algorithm, structured perceptron, and learning to search through approaches like SEARN and DAgger for efficient predictions and decision-making in complex structured outputs. The conclusion outlines how these techniques can apply to fine-tuning predictions based on ground truth representations in graph summarization tasks.

1. SUPERVISED PREDICTION
OF GRAPH SUMMARIES
Daniil Mirylenka
University of Trento, Italy
1

2. Outline
• Motivating example (from my Ph.D. research)
• Supervised learning
• Binary classification
• Perceptron
• Ranking, Multiclass
• Structured output prediction
• General approach, Structured Perceptron
• “Easy” cases
• Prediction as search
• Searn, DAGGER
• Back to the motivating example
2

3. Motivating example
Representing academic search results
3
graph summary
search results

4. Motivating example
Suppose we can do this:
4
large graph

5. Motivating example
Then we only need to do this:
5
small graph

6. Motivating example
What is a good graph summary?
Let’s learn from examples!
6

7. Supervised learning
7

8. What is supervised learning?
x1, y1( ), x2, y2( ), …, xn, yn( )
f : x ! y
8
Supervised
Learning
bunch of
examples
function

9. x1, y1( ), x2, y2( ), …, xn, yn( )
9
distribution of examples
Statistical learning theory
P(x,y)
Where do our examples come from?
samples drawn i.i.d.

10. 10
hypothesis space
Statistical learning theory
What functions do we consider?
f ∈ H
linear?
H1
cubic?
H2
piecewise-linear?
H3

11. 11
loss function
Statistical learning theory
How bad is it to predict instead of (true) ?f x( ) y
L f x( ), y( )
L y, !y( )=
0, when y = !y
1, otherwise
"
#
$
Example: zero-one loss

12. Statistical learning theory
argmin
f ∈H
L( f (x), y)p(x, y)dxdy
X×Y
∫
Goal:
Requirement:
argmin
f ∈H
L( f (xi ), yi )
i=1
n
∑
12
expected loss
on new examples
total loss on
training data

13. Linear models
w = argmin
w
L( fw x( ), yi )
i=1
n
∑
Inference (prediction):
fw x( )= g( w,ϕ x( ) )
optimization with respect to w
(e.g. gradient descent)
Learning:
13
features of x scalar product
(linear combination,
weighted sum)
H

14. Binary classification
y ∈ {−1,1}
Prediction: fw x( )= sign( w, x )
14
above or below the
line (hyperplane)?
yi w, xi > 0
Note that:
w, x > 0
w, x < 0
w, x = 0

15. Perceptron
Learning algorithm
(optimizes one example at a time)
For every xi
if yi w, xi ≤ 0
w ← w + yi xi
• if made a mistake
• update the weights
if yi>0 makes wi+1 more like xi
if yi<0 makes wi+1 more like -xi
15
Repeat

16. Perceptron
Update rule:
wold
16
xi
w ← w + yi xi

17. Perceptron
wold
17
xi
wnew
Update rule: w ← w + yi xi

18. Max-margin classification
Idea: ensure some distance form the hyperplane
18
yi w, xi ≥1
Require:

19. Preference learning
Suppose we want to predict rankings: x ! y =
v1
v2
"
vk
x,vi( )≻ x,vj( )⇔ i < j
19
joint features of x and v
w
ϕ x,v1( )
ϕ x,v2( )
ϕ x,v3( )
ϕ x,v4( )
ϕ x,v5( )
Also works for:
• selecting just the best one
• multiclass classification
w,ϕ x,v( )−ϕ x, "v( ) ≥1

20. Structured prediction
20

21. Structured prediction
Examples:
• “Time flies like an arrow.”x =
part-of-speech tagging
• (noun verb preposition determiner noun)!y =
• (S (NP (NNP Time))
(VP (VBZ flies)
(PP (IN like)
(NP (DT an)
(NN arrow)))))
y =
parse tree
or
21

22. Structured prediction
How can we approach this problem?
f x( )= g w,ϕ x( )( )• before we had:
• now must be a complex objectf x( )
f x( )= argmax
y
w,ψ x, y( )( )
joint features of x and y
(kind of like we had with ranking)
22

23. Structured Perceptron
Almost the same as ordinary perceptron
• For every xi
• if ˆyi ≠ yi
w ← w +ψ xi, yi( )−ψ xi, ˆyi( )
(if made a mistake)
update the weights
• predict: ˆyi = argmax
y
w,ψ xi, y( )( )
•
23

24. Argmax problem
often infeasible
ˆy = argmax
y
w,ψ x, y( )( )
Prediction:
Examples:
24
• sequence of length T, with d options for each label: dT
• a subgraph of size T from a graph G: |G| chose T
• 10-word sentence, 5 parts of speech: ~10 million outputs
• 10-node subgraph of a 300-node graph:
1,398,320,233,231,701,770 outputs (around 1018)

25. Argmax problem
ˆy = argmax
y
w,ψ x, y( )( )
Prediction:
Learning:
• even more difficult
• includes prediction as a subroutine
25
often infeasible

26. Argmax problem: easy cases
Independent prediction
• suppose decomposes into
• and decomposes into
y v1,v2,…,vT( )
ψ x, y( )= ψi x,vi( )
i=1
T
∑
ψ x, y( )
argmax
y
w,ψ x, y( ) =
argmax
v1
w,ψ1 x,v1( ) ,…,argmax
vn
w,ψn x,vn( )
!
"
#
$
%
&
• then predictions can be made independently
26

27. Argmax problem: easy cases
Sequence labeling
• suppose decomposes into
• and decomposes into
y v1,v2,…,vT( )
ψ x, y( )= ψi x,vi,vi+1( )
i=1
T−1
∑
ψ x, y( )
• dynamic programming : O(Td2)
27
• with ternary features : O(Td3), etc.
• in general tractable in graphs with bounded treewidth

28. Approximate argmax
General idea:
• search
in the space of outputs
Natural generalization:
• space of partial outputs
• composing the solution
sequentially
Let’s learn to make good moves!
How do we decide which moves to take?
Most interesting/crazy
idea of this talk
(And we don’t need the original argmax problem anymore)
28

29. Learning to search
29

30. Learning to search
Sequential prediction of structured outputs
y = v1,v2,…,vT( )• decompose the output
π : v1,v2,…,vt( )→ vt+1• learn the policy
state action
s0
π
! →! s1
π
! →! … π
! →! sT = y
• apply the policy sequentially
st → vt+1
• policy can be trained on examples st,vt+1( )
• preference learning
30

31. Learning to search
The caveat of sequential prediction
siStates : coordinates of the car
Actions : steering (‘left’, ‘right’)vi+1
Oops!
left!
left!
right!
right!
left!
Problem:
• errors accumulate
• training data is not i.i.d.!
Solution:
• Train on the states produced by our policy!
Chicken-and-egg problem
(solution: iterate)
31

32. Searn and DAGGER
Searn = “search” + “learn”
• start from optimal policy;
move away
• generate new states with current
• generate actions based on regret
• train on new state-action pairs
• interpolate the current policy
πi+1 ← βπi + 1− β( ) #πi+1
policy learnt at ith iteration
regret
32
[1] Hal Daumé III, John Langford, Daniel Marcu. Search-based Structured Prediction. Machine Learning Journal, 2006.
[1]
!πi+1
πi

33. Searn and DAGGER
DAGGER = “dataset” + “aggregation”
• start from the ‘ground truth’ dataset,
enrich it with new state-action pairs
• train a policy on the current dataset
• use the policy to generate new states
• generate ‘expert’s actions’ for new states
• add new state-action pairs to the dataset
expert’s
actions
As in Searn, we’ll eventually be training
on our own-produced states
33
[2] Stephane Ross, Geoffrey Gordon, Drew Bagnell. A reduction of imitation learning and
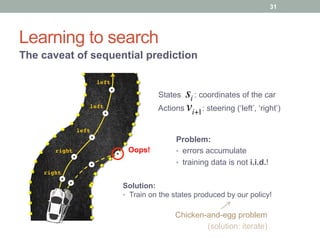
structured prediction to no-regret online learning. Journal of Machine Learning Research, 2011.
[2]

34. DAGGER for building the graph summaries
Input: topic graph ,
search results ,
relation
Output: topic summary of size
G V, E( )
R ⊆ V × S
S
GT VT , ET( ) T
A few tricks:
• Predict only vertices ,VT
• Require that the summaries be nested:
• which means
• hence, the task is to predict the sequence
∅ =V0 ⊂ V1 ⊂…⊂ VT
Vi+1 =Vi + vi+1
v1,v2,…,vT( )
34

35. DAGGER for building the graph summaries
• Provide the ‘ground truth’ topic sequences
V,S, R( ),v1,v2,…,vT( ) a single ground truth example
topics (vertices)
documents
(search results)
topic-document
relations
topic sequence
• Create the dataset D0 = ∪ si,vi+1( ){ }i=0
T
• train the policy onπi Di
• apply to the initial states to generate state sequencesπi
s0
s1,s2,…,sT( )
empty summary
intermediate summaries
• produce the ‘expert action’ for every generated state
• produce
v*
Di+1 = Di ∪ s,v*
( ){ }
35

36. DAGGER: producing the ‘expert action’
• The expert’s action brings us closer
to the ‘ground-truth’ trajectory
expert’s
actions
• Suppose the ‘ground-truth’ trajectory is
36
s1,s2,…,sT( )
• And the generated trajectory is
ˆs1, ˆs2,…, ˆsT( )
• The expert’s action
vi+1
*
= argmin
v
Δ ˆsi ∪ v{ },si+1( )( )
dissimilarity between the states

37. DAGGER: topic sequence dissimilarity
• Set-based dissimilarity, e.g. Jaccard distance
• similarity between topics ?
• encourages redundancy
• Sequence-matching based dissimilarity
• greedy approximation
37
Δ v1,v2,…,vt( ), !v1, !v2,…, !vt( )( )

38. DAGGER: topic graph features
• Coverage and diversity
• [transitive] document coverage
• [transitive] topic frequency, average and min
• topic overlap, average and max
• parent-child overlap, average and max
• …
38
ψ V,S, R( ), v1,v2,…,vt( )( )

39. Recap
• We’ve learnt:
• … how to do binary classification
• and implement it in 4 lines of code
• … about more complex problems
(ranking, and structured prediction)
• general approach, structured Perceptron
• argmax problem
• … that learning and search are two sides of the same coin
• … how to predict complex structures by building them sequentially
• Searn and DAGGER
39

40. Questions?
40
dmirylenka @ disi.unitn.it

41. Extra slides
41

42. Support Vector Machine
Idea: large margin between positive and negative examples
Loss function:
L y, f x( )( )=[1− y⋅ f x( )]+
Hinge loss
(solved by constrained convex optimization)
yi w, xi ≥ C
C → max
#
$
%
&%
⇔
yi w, xi ≥1
w → min
#
$
%
&%
42

43. Structured SVM
correct outputs score higher by a margin
w → min
w,ψ xi, y( ) − w,ψ xi, yi( ) ≥1, yi ≠ y
w,ψ xi, yi( )−ψ xi, y( ) ≥ Δ yi, y( ), yi ≠ y
margin depends on dissimilarity
Taking into account (dis)similarity between the outputs
43