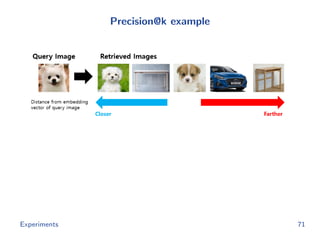
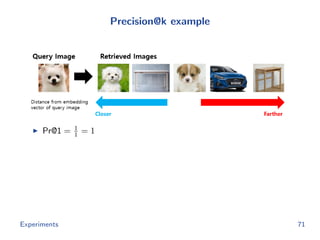
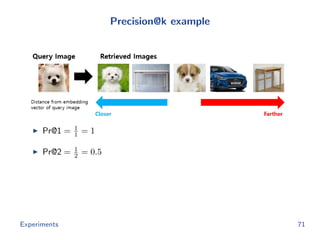
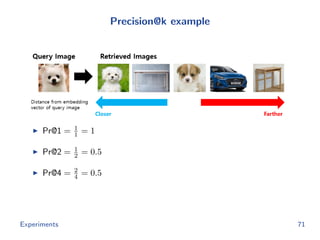
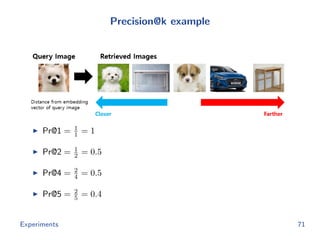
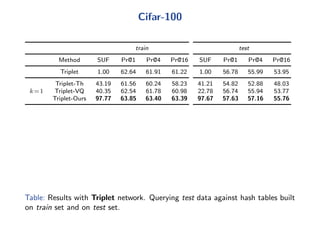
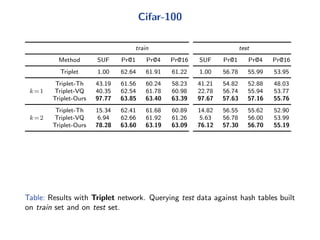
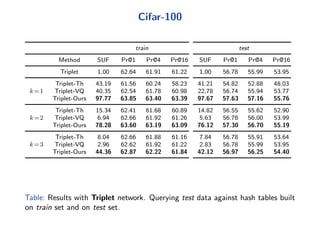
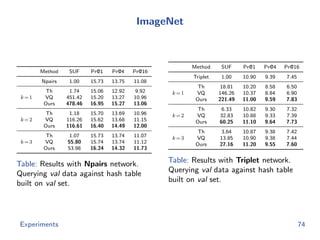
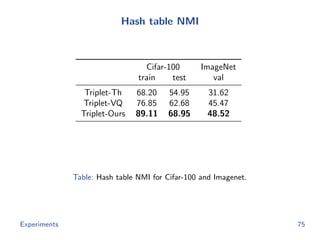
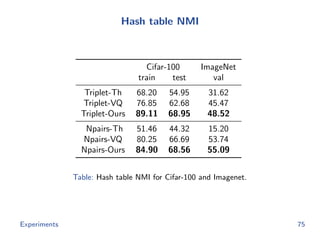
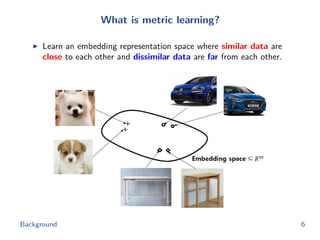
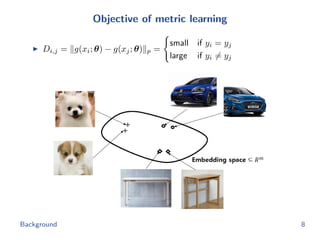
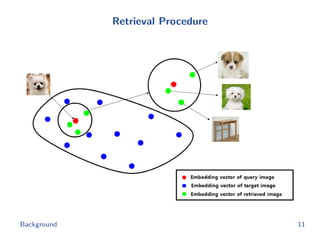
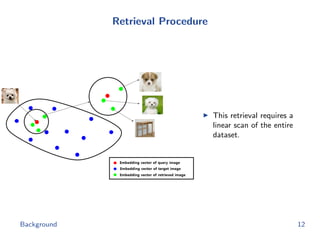
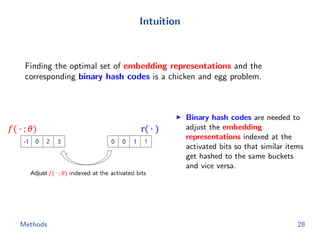
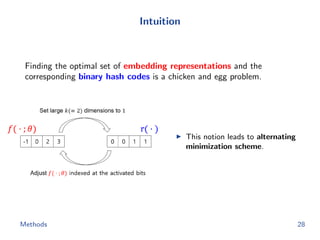
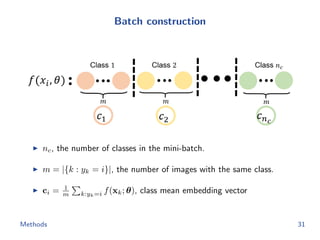
The document discusses efficient end-to-end learning for quantizable representation, focusing on the challenges of image classification with numerous labels and the role of metric learning in addressing these challenges. It presents various methods, including triplet loss and npairs loss, to optimize embedding representations and corresponding binary hash codes, utilizing an alternating minimization framework. The document also outlines experiments comparing proposed methods against baseline approaches to evaluate performance.

1. Efficient end-to-end learning for quantizable
representation
Yeonwoo Jeong, Hyun Oh Song
Dept. of Computer Science and Engineering, Seoul National University
July 25, 2018
1

2. Outline
Background
Problem formulation
Methods
Experiments
Conclusion
Background 2

3. Classification
The objective of classification problem is to classify the images into
one of the predefined labels.
Background 3

4. The limitation of classifications
Classification with a large number of labels is a difficult problem.
e.g. Human faces with 7 billion labels
Background 4

5. The limitation of classifications
We have to train classifier again for the data with a new label.
Then, the notion of metric learning comes out.
Background 5

6. What is metric learning?
Learn an embedding representation space where similar data are
close to each other and dissimilar data are far from each other.
Background 6

7. Notation
X = {x1, · · · , xn} is a set of images and xi ∈ X is an image.
yi ∈ {0, 1, · · · , C − 1} is a class of image xi where C is the number
of classes.
g : X → Rm
is the embedding function where m is the embedding
dimension.
θ is the parameter to be learned in g( · ; θ)
Background 7

8. Objective of metric learning
Di,j = g(xi; θ) − g(xj; θ) p =
small if yi = yj
large if yi = yj
Background 8

9. Retrieval Procedure
Background 9

10. Retrieval Procedure
Background 10

11. Retrieval Procedure
Background 11

12. Retrieval Procedure
This retrieval requires a
linear scan of the entire
dataset.
Background 12

13. Triplet loss1
T = {(a, p, n) | ya = yp = yn}
: a set of triplets(anchor, positive, negative)
In the desired representation,
1. Da,p is small, anchor is close to positive.
2. Da,n is large, anchor is far from negative.
1F. Schroff, D. Kalenichenko, and J.Philbin. “Facenet: A unified embedding for face
recognition and clustering“. CVPR2015.
Background 13

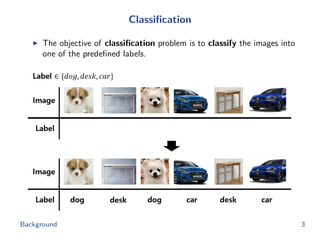
14. Triplet loss
(X, y) =
1
T
(a,p,n)∈T
[D2
a,p + α − D2
a,n]+
X : a set of images
y : a set of classes
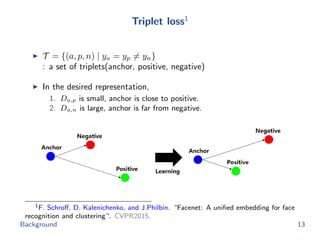
T : a set of triplets(anchor, positive, negative)
α : a margin which is constant
[·]+ = max(·, 0)
Training process reduces l(X, y) decreasing Da,p and increasing Da,n.
Background 14

15. Npairs loss2
There are multiple negatives with an anchor and a positive.
The objective is to reduce the distance between the anchor and the
positive increasing the distance between the anchor and negatives.
2K. Sohn. “Improved deep metric learning with multi-class n-pair loss objective“.
NIPS2016.
Background 15

16. Npairs loss
(X, y) = −
1
P
(i,j)∈P
log
exp (−Di,j)
exp (−Di,j) + k:yk=yi
exp (−Di,k)
+
λ
i
f(xi; θ) 2
2
P = {(i, j) | yi = yj} : a set of pairs with the same label
i f(xi; θ) 2
2 : the regularizer term
Training process reduces l(X, y) decreasing Di,j with yi = yj and
increasing Di,k with yi = yk.
Background 16

17. Outline
Background
Problem formulation
Methods
Experiments
Conclusion
Problem formulation 17

18. Hash function
f( · ; θ) : X → Rd
is a differentiable transformation with respect to
parameter θ.
Problem formulation 18

19. Hash function
f( · ; θ) : X → Rd
is a differentiable transformation with respect to
parameter θ.
r(·) sets large k elements in f( · ; θ) to be 1, otherwise 0.
e.g.
k=2, f(x; θ) = (−2, 7, 3, 1)
⇒ r(x) = (0, 1, 1, 0)
Problem formulation 18

20. Hash function
f( · ; θ) : X → Rd
is a differentiable transformation with respect to
parameter θ.
r(·) sets large k elements in f( · ; θ) to be 1, otherwise 0.
e.g.
k=2, f(x; θ) = (−2, 7, 3, 1)
⇒ r(x) = (0, 1, 1, 0)
r(·) : X → {0, 1}d
, r(·) 1 = k
r(x) = argmin
h∈{0,1}d
−f(x; θ) h
subject to h 1 = k
Problem formulation 18

21. Hash table construction
Problem formulation 19

22. Hash table construction
Problem formulation 20

23. Hash table construction
Problem formulation 21

24. Hash table construction
Problem formulation 22

25. Hash table construction
Problem formulation 23

26. Query on the hash table
Problem formulation 24

27. Query on the hash table
Problem formulation 25

28. Query on the hash table
Problem formulation 26

29. Outline
Background
Problem formulation
Methods
Experiments
Conclusion
Methods 27

30. Intuition
Finding the optimal set of embedding representations and the
corresponding binary hash codes is a chicken and egg problem.
Methods 28

31. Intuition
Finding the optimal set of embedding representations and the
corresponding binary hash codes is a chicken and egg problem.
Embedding representations are
required to infer which k activation
dimensions to set in the binary
hash code.
Methods 28

32. Intuition
Finding the optimal set of embedding representations and the
corresponding binary hash codes is a chicken and egg problem.
Binary hash codes are needed to
adjust the embedding
representations indexed at the
activated bits so that similar items
get hashed to the same buckets
and vice versa.
Methods 28

33. Intuition
Finding the optimal set of embedding representations and the
corresponding binary hash codes is a chicken and egg problem.
This notion leads to alternating
minimization scheme.
Methods 28

34. Alternating minimization scheme
minimize
θ
h1,...,hn
metric({f(xi; θ)}n
i=1; h1, . . . , hn)
embedding representation quality
+γ


n
i
−f(xi; θ) hi +
n
i j:yj =yi
hi Phj


hash code performance
subject to hi ∈ {0, 1}d
, ||hi||1 = k, ∀i,
Solving for binary hash codes h1:n with sparsity k
Updating θ, the parameter in deep neural network.
Methods 29

35. Solving for binary hash codes h1:n
minimize
h1,...,hn
n
i
−f(xi; θ) hi
unary term
+
n
i j:yj =yi
hi Phj
pairwise term
subject to hi ∈ {0, 1}d
, ||hi||1 = k, ∀i,
Unary term encourages to select k large elements in embedding
vector(f( · ; θ)).
Methods 30

36. Solving for binary hash codes h1:n
minimize
h1,...,hn
n
i
−f(xi; θ) hi
unary term
+
n
i j:yj =yi
hi Phj
pairwise term
subject to hi ∈ {0, 1}d
, ||hi||1 = k, ∀i,
Unary term encourages to select k large elements in embedding
vector(f( · ; θ)).
Pairwise term selects as orthogonal elements as possible across
between different classes.
Methods 30

37. Solving for binary hash codes h1:n
minimize
h1,...,hn
n
i
−f(xi; θ) hi
unary term
+
n
i j:yj =yi
hi Phj
pairwise term
subject to hi ∈ {0, 1}d
, ||hi||1 = k, ∀i,
Unary term encourages to select k large elements in embedding
vector(f( · ; θ)).
Pairwise term selects as orthogonal elements as possible across
between different classes.
NP-hard problem even in simple case k = 1, d > 2
Methods 30

38. Batch construction
nc, the number of classes in the mini-batch.
m = |{k : yk = i}|, the number of images with the same class.
ci = 1
m k:yk=i f(xk; θ), class mean embedding vector
Methods 31

39. Optimizing within a batch
n
i
−f(xi; θ) hi +
n
i j:yj =yi
hi Phj
=
nc
i k:yk=i
−f(xk; θ) hk +
nc
i k:yk=i,
l:yl=i
hkPhl
Methods 32

40. Upper bound
nc
i k:yk=i
−f(xk; θ) hk +
nc
i k:yk=i,
l:yl=i
hkPhl
≤
nc
i k:yk=i
−ci hk +
nc
i k:yk=i,
l:yl=i
hkPhl + M(θ)
where M(θ) = maximize
h1,...,hn
hi∈{0,1}d
,||hi||1=k
nc
i=1 k:yk=i
(ci − f(xk; θ)) hk
The bound gap M(θ) decreases as we update θ to attract similar
pairs of data and vice versa for dissimilar pairs.
Methods 33

41. Equivalence of minimizing the upper bound
minimize
h1,...,hn
hi∈{0,1}d
,||hi||1=k
nc
i k:yk=i
−ci hk +
nc
i k:yk=i,
l:yl=i
hkPhl
= minimizez1,...,znc
zi∈{0,1}d
,||zi||1=k
m


nc
i
−ci zi +
nc
i j=i
zi P zj


:= ˆg(z1,...,nc ;θ)
,
P = mP
Methods 34

42. Discrete optimization problem
minimize
z1,...,znc
nc
i=1
−ci zi +
i,j=i
zi Pzj
subject to zi ∈ {0, 1}d
, ||zi||1 = k, ∀i
P = diag (λ1, · · · , λd)
Methods 35

43. Minimum-cost flow problem
G = (V, E) is a directed graph with a source and sink s, t ∈ V
Methods 36

44. Minimum-cost flow problem
G = (V, E) is a directed graph with a source and sink s, t ∈ V
Capacity is a maximum possible flow for e ∈ E.
Cost is the cost required when flow passes e ∈ E.
Methods 36

45. Minimum-cost flow problem
G = (V, E) is a directed graph with a source and sink s, t ∈ V
Capacity is a maximum possible flow for e ∈ E.
Cost is the cost required when flow passes e ∈ E.
The amount of flow d to be sent from source s to sink t
Methods 36

46. Minimum-cost flow problem
minimize
e∈E
v(e)f(e)
f(e) ≤ u(e) (capacity constraint)
i:(i,u)∈E
f(i, u) =
j:(u,j)∈E
f(u, j) (flow conservation for u = s, t ∈ E)
j:(s,j)∈E
f(s, j) = d (flow conservation for source s)
j:(j,t)∈E
f(j, t) = d (flow conservation for source t)
Methods 37

47. Minimum-cost flow problem example
Every edges have capacity on the left and cost on the right in the
figure.
Methods 38

48. Minimum-cost flow problem example
The amount of flow d to be sent from source s to sink t is 3.
For the optimal feasible flow,
total cost = 1 × 1 + 2 × 2 + 3 × 1 + 1 × 3 = 11
Methods 39

49. Theorem
minimize
z1,··· ,znc
nc
p=1
−cpzp +
p1=p2
zp1
Pzp2
subject to zp ∈ {0, 1}d
, zp 1 = k, ∀i
(1)
P = diag (λ1, · · · , λd)
The optimization problem can be solved by finding the minimum cost
flow solution on the flow network G’.
Methods 40

50. Flow network
Figure: Equivalent flow network diagram G for the optimization problem.
Labeled edges show the capacity and the cost, respectively. The amount of
total flow to be sent is nck.
Methods 41

51. Flow network construction
|A| = nc.
|B| = d(= 5).
A = {a1, a2, a3}.
B = {b1, · · · , b5}.
Methods 42

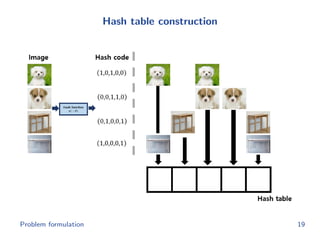
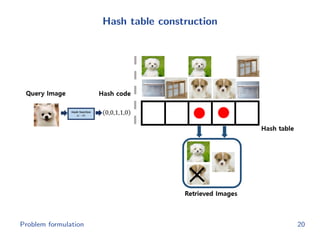
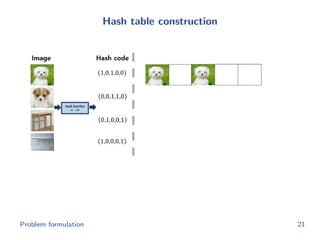
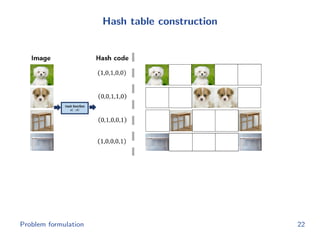
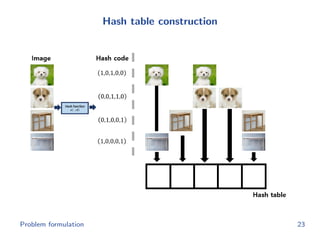
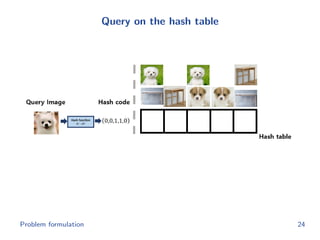
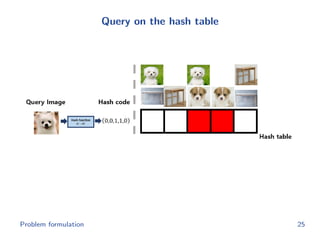
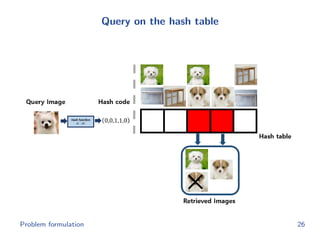
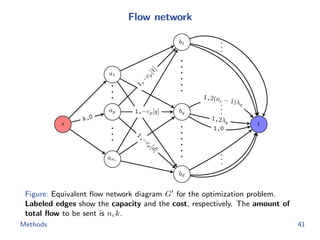
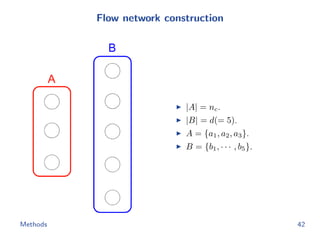
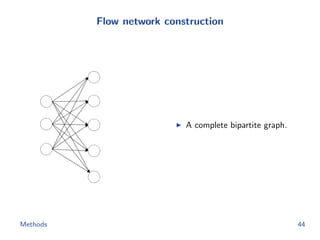
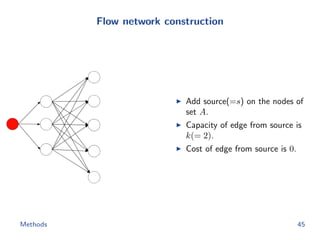
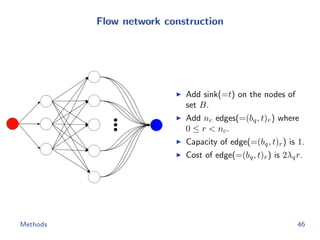
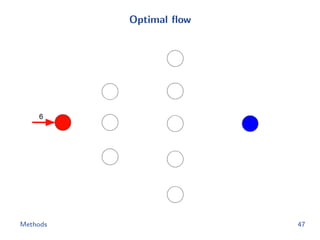
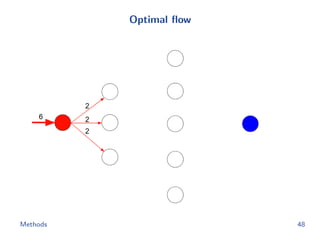
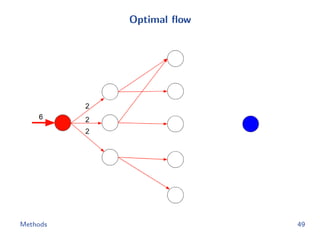
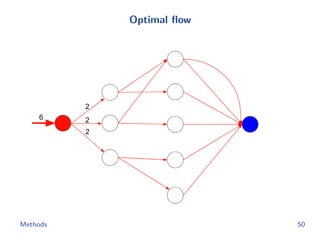
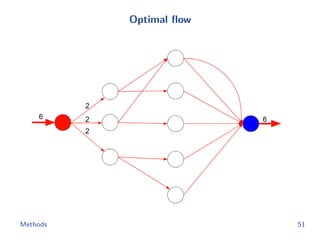
52. Flow network construction
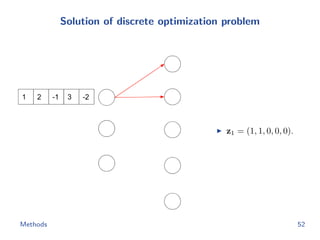
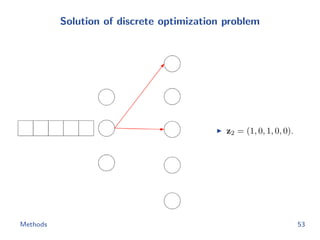
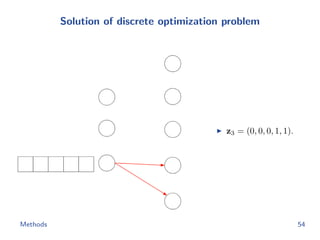
c1 = (1, 2, −1, 3, −2)
Capacity of every edge is 1.
Cost of edge(=(ap, bq)) is
−cp[q].
Methods 43

53. Flow network construction
A complete bipartite graph.
Methods 44

54. Flow network construction
Add source(=s) on the nodes of
set A.
Capacity of edge from source is
k(= 2).
Cost of edge from source is 0.
Methods 45

55. Flow network construction
Add sink(=t) on the nodes of
set B.
Add nc edges(=(bq, t)r) where
0 ≤ r < nc.
Capacity of edge(=(bq, t)r) is 1.
Cost of edge(=(bq, t)r) is 2λqr.
Methods 46

56. Optimal flow
Methods 47

57. Optimal flow
Methods 48

58. Optimal flow
Methods 49

59. Optimal flow
Methods 50

60. Optimal flow
Methods 51

61. Solution of discrete optimization problem
z1 = (1, 1, 0, 0, 0).
Methods 52

62. Solution of discrete optimization problem
z2 = (1, 0, 1, 0, 0).
Methods 53

63. Solution of discrete optimization problem
z3 = (0, 0, 0, 1, 1).
Methods 54

64. Time complexity
We solve minimum cost flow problem within the mini-batch not
on the entire dataset.
The practical running time is O (ncd).
Methods 55

65. Time complexity
64 128 256 512
0
0.5
1
1.5
d
Averagewallclockruntime(sec)
nc = 64
nc = 128
nc = 256
nc = 512
Figure: Average wall clock run time of computing minimum cost flow on G per
mini-batch using ortools. In practice, the run time is approximately linear in nc
and d. Each data point is averaged over 20 runs on machines with Intel Xeon
E5-2650 CPU.
Methods 56

66. Define the distance
Embedding vectors f(xi; θ), f(xj; θ)
k-sparse binary hash codes hi, hj
Methods 57

67. Define the distance
Embedding vectors f(xi; θ), f(xj; θ)
k-sparse binary hash codes hi, hj
d hash
ij = (hi ∨ hj) (f(xi; θ) − f(xj; θ)) 1
∨ : logical or operation of the two binary codes.
: the element-wise multiplication.
Methods 57

68. Define the distance
Embedding vectors f(xi; θ), f(xj; θ)
k-sparse binary hash codes hi, hj
d hash
ij = (hi ∨ hj) (f(xi; θ) − f(xj; θ)) 1
∨ : logical or operation of the two binary codes.
: the element-wise multiplication.
Define metric({f(xi; θ)}n
i=1; h1, . . . , hn) with dhash
ij
(e.g. triplet loss, npairs loss).
Methods 57

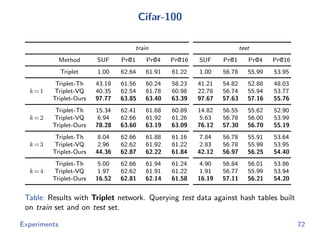
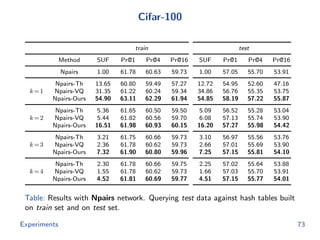
69. Metric learning losses
Triplet loss
minimize
θ
1
|T |
(i,j,k)∈T
[d hash
ij + α − d hash
ik ]+
triplet(θ; h1,...,n)
subject to ||f(x; θ)||2 = 1
We apply the semi-hard negative mining to construct triplet.
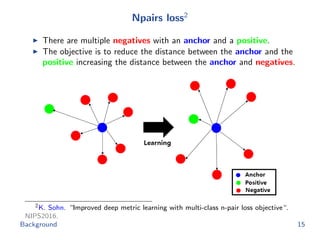
Npairs loss
minimize
θ
−1
|P|
(i,j)∈P
log
exp(−d hash
ij )
exp(−d hash
ij ) + k:yk=yi
exp(−d hash
ik )
npairs(θ; h1,...,n)
+
λ
m i
||f(xi; θ)||2
2
Methods 58

70. Pseudocode
Methods 59

71. Outline
Background
Problem formulation
Methods
Experiments
Conclusion
Experiments 60

72. Baselines
There are two baselines ’Th’ and ’VQ’.
’Th’ is a binarization transform method34
.
’VQ’ is a vector quantization method5
.
3P. Agrawal, R. Girshick, and J. Malik. “Analyzing the performance of multilayer
neural networks for object recognition“. ECCV2014.
4A. Zhai, D. Kislyuk, Y. Jing, M. Feng, E. Tzeng, J. Donahue, Y. L. Du, and T.
Darrell. “Visual discovery at pinterest“. WWW2017.
5J. Wang, T. Zhang, J. Song, N. Sebe, and H. T. Shen. “A survey on learning to
hash“. TPAMI2017.
Experiments 61

73. Baselines
Let g( · ; θ ) ∈ Rm
be the embedding representation trained with
deep metric learning losses(e.g. triplet loss, npairs loss).
For fair comparision, m = d.
The embedding dimension of f(x; θ) is same with that of g(x; θ ).
Denote t1, · · · , td, the d centroids of k-means clustering in
{g(xi; θ ) ∈ Rm
| xi ∈ X}.
Experiments 62

74. Baselines
The hash code of image x from ’Th’ method is
rTh(x) = argmin
h∈{0,1}m
−g(x; θ ) h
subject to h 1 = k
cf.
rOurs(x) = argmin
h∈{0,1}d
−f(x; θ) h
subject to h 1 = k
Experiments 63

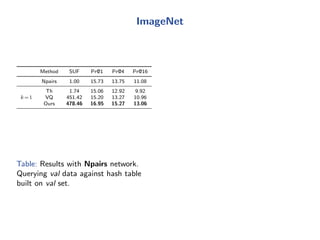
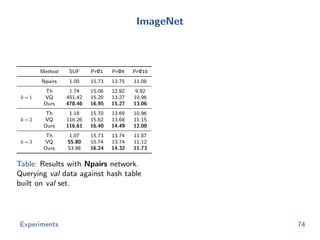
75. Baselines
The hash code of image x from ’Th’ method is
rTh(x) = argmin
h∈{0,1}m
−g(x; θ ) h
subject to h 1 = k
cf.
rOurs(x) = argmin
h∈{0,1}d
−f(x; θ) h
subject to h 1 = k
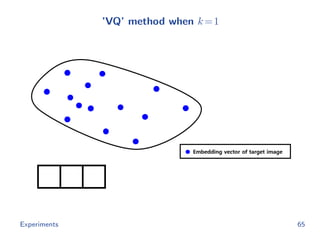
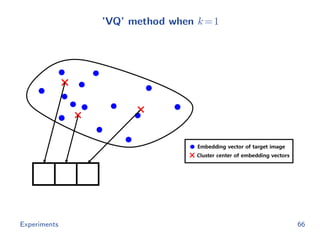
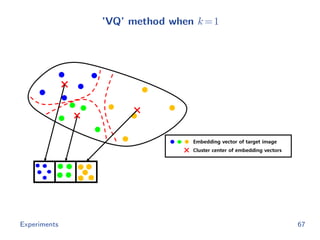
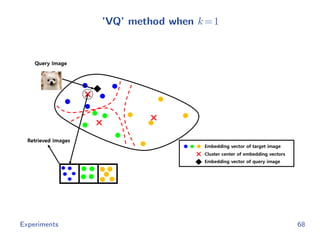
The hash code of image x from ’VQ’ method is
rVQ(x) = argmin
h∈{0,1}d
[ g(x; θ ) − t1 2, · · · , g(x; θ ) − td 2]h
subject to h 1 = k
Experiments 63

76. ’VQ’
’VQ’ method is usually used in the industry.
However, ’VQ’ becomes unpractical as |X| increases.
Experiments 64

77. ’VQ’ method when k=1
Experiments 65

78. ’VQ’ method when k=1
Experiments 66

79. ’VQ’ method when k=1
Experiments 67

80. ’VQ’ method when k=1
Experiments 68

81. Evaluation metric
’NMI’ is normalized mutual information which measures clustering
quality when k=1 treating each bucket as an individual cluster.
’Pr@k’ is precision@k which is computed based on the reranking based
on g(x; θ ) after the retrieval with hash codes.
Experiments 69

82. Evaluation metric
Let R(q, k, X) be the top-k retrieved images in X when the query
image is q.
Let Q be the set of query images.
Denote labelq and labelx, label of query q and label of image x
respectively.
Pr@k =
1
|Q|
q∈Q
|{labelq = labelx | x ∈ R(q, k, X)}|
k
Experiments 70

83. Precision@k example
Experiments 71

84. Precision@k example
Pr@1 = 1
1 = 1
Experiments 71

85. Precision@k example
Pr@1 = 1
1 = 1
Pr@2 = 1
2 = 0.5
Experiments 71

86. Precision@k example
Pr@1 = 1
1 = 1
Pr@2 = 1
2 = 0.5
Pr@4 = 2
4 = 0.5
Experiments 71

87. Precision@k example
Pr@1 = 1
1 = 1
Pr@2 = 1
2 = 0.5
Pr@4 = 2
4 = 0.5
Pr@5 = 2
5 = 0.4
Experiments 71

88. Cifar-100
train test
Method SUF Pr@1 Pr@4 Pr@16 SUF Pr@1 Pr@4 Pr@16
Triplet 1.00 62.64 61.91 61.22 1.00 56.78 55.99 53.95
k=1
Triplet-Th 43.19 61.56 60.24 58.23 41.21 54.82 52.88 48.03
Triplet-VQ 40.35 62.54 61.78 60.98 22.78 56.74 55.94 53.77
Triplet-Ours 97.77 63.85 63.40 63.39 97.67 57.63 57.16 55.76
Table: Results with Triplet network. Querying test data against hash tables built
on train set and on test set.

89. Cifar-100
train test
Method SUF Pr@1 Pr@4 Pr@16 SUF Pr@1 Pr@4 Pr@16
Triplet 1.00 62.64 61.91 61.22 1.00 56.78 55.99 53.95
k=1
Triplet-Th 43.19 61.56 60.24 58.23 41.21 54.82 52.88 48.03
Triplet-VQ 40.35 62.54 61.78 60.98 22.78 56.74 55.94 53.77
Triplet-Ours 97.77 63.85 63.40 63.39 97.67 57.63 57.16 55.76
k=2
Triplet-Th 15.34 62.41 61.68 60.89 14.82 56.55 55.62 52.90
Triplet-VQ 6.94 62.66 61.92 61.26 5.63 56.78 56.00 53.99
Triplet-Ours 78.28 63.60 63.19 63.09 76.12 57.30 56.70 55.19
Table: Results with Triplet network. Querying test data against hash tables built
on train set and on test set.

90. Cifar-100
train test
Method SUF Pr@1 Pr@4 Pr@16 SUF Pr@1 Pr@4 Pr@16
Triplet 1.00 62.64 61.91 61.22 1.00 56.78 55.99 53.95
k=1
Triplet-Th 43.19 61.56 60.24 58.23 41.21 54.82 52.88 48.03
Triplet-VQ 40.35 62.54 61.78 60.98 22.78 56.74 55.94 53.77
Triplet-Ours 97.77 63.85 63.40 63.39 97.67 57.63 57.16 55.76
k=2
Triplet-Th 15.34 62.41 61.68 60.89 14.82 56.55 55.62 52.90
Triplet-VQ 6.94 62.66 61.92 61.26 5.63 56.78 56.00 53.99
Triplet-Ours 78.28 63.60 63.19 63.09 76.12 57.30 56.70 55.19
k=3
Triplet-Th 8.04 62.66 61.88 61.16 7.84 56.78 55.91 53.64
Triplet-VQ 2.96 62.62 61.92 61.22 2.83 56.78 55.99 53.95
Triplet-Ours 44.36 62.87 62.22 61.84 42.12 56.97 56.25 54.40
Table: Results with Triplet network. Querying test data against hash tables built
on train set and on test set.

91. Cifar-100
train test
Method SUF Pr@1 Pr@4 Pr@16 SUF Pr@1 Pr@4 Pr@16
Triplet 1.00 62.64 61.91 61.22 1.00 56.78 55.99 53.95
k=1
Triplet-Th 43.19 61.56 60.24 58.23 41.21 54.82 52.88 48.03
Triplet-VQ 40.35 62.54 61.78 60.98 22.78 56.74 55.94 53.77
Triplet-Ours 97.77 63.85 63.40 63.39 97.67 57.63 57.16 55.76
k=2
Triplet-Th 15.34 62.41 61.68 60.89 14.82 56.55 55.62 52.90
Triplet-VQ 6.94 62.66 61.92 61.26 5.63 56.78 56.00 53.99
Triplet-Ours 78.28 63.60 63.19 63.09 76.12 57.30 56.70 55.19
k=3
Triplet-Th 8.04 62.66 61.88 61.16 7.84 56.78 55.91 53.64
Triplet-VQ 2.96 62.62 61.92 61.22 2.83 56.78 55.99 53.95
Triplet-Ours 44.36 62.87 62.22 61.84 42.12 56.97 56.25 54.40
k=4
Triplet-Th 5.00 62.66 61.94 61.24 4.90 56.84 56.01 53.86
Triplet-VQ 1.97 62.62 61.91 61.22 1.91 56.77 55.99 53.94
Triplet-Ours 16.52 62.81 62.14 61.58 16.19 57.11 56.21 54.20
Table: Results with Triplet network. Querying test data against hash tables built
on train set and on test set.
Experiments 72

92. Cifar-100
train test
Method SUF Pr@1 Pr@4 Pr@16 SUF Pr@1 Pr@4 Pr@16
Npairs 1.00 61.78 60.63 59.73 1.00 57.05 55.70 53.91
k=1
Npairs-Th 13.65 60.80 59.49 57.27 12.72 54.95 52.60 47.16
Npairs-VQ 31.35 61.22 60.24 59.34 34.86 56.76 55.35 53.75
Npairs-Ours 54.90 63.11 62.29 61.94 54.85 58.19 57.22 55.87
k=2
Npairs-Th 5.36 61.65 60.50 59.50 5.09 56.52 55.28 53.04
Npairs-VQ 5.44 61.82 60.56 59.70 6.08 57.13 55.74 53.90
Npairs-Ours 16.51 61.98 60.93 60.15 16.20 57.27 55.98 54.42
k=3
Npairs-Th 3.21 61.75 60.66 59.73 3.10 56.97 55.56 53.76
Npairs-VQ 2.36 61.78 60.62 59.73 2.66 57.01 55.69 53.90
Npairs-Ours 7.32 61.90 60.80 59.96 7.25 57.15 55.81 54.10
k=4
Npairs-Th 2.30 61.78 60.66 59.75 2.25 57.02 55.64 53.88
Npairs-VQ 1.55 61.78 60.62 59.73 1.66 57.03 55.70 53.91
Npairs-Ours 4.52 61.81 60.69 59.77 4.51 57.15 55.77 54.01
Table: Results with Npairs network. Querying test data against hash tables built
on train set and on test set.
Experiments 73

93. ImageNet
Method SUF Pr@1 Pr@4 Pr@16
Npairs 1.00 15.73 13.75 11.08
k=1
Th 1.74 15.06 12.92 9.92
VQ 451.42 15.20 13.27 10.96
Ours 478.46 16.95 15.27 13.06
Table: Results with Npairs network.
Querying val data against hash table
built on val set.

94. ImageNet
Method SUF Pr@1 Pr@4 Pr@16
Npairs 1.00 15.73 13.75 11.08
k=1
Th 1.74 15.06 12.92 9.92
VQ 451.42 15.20 13.27 10.96
Ours 478.46 16.95 15.27 13.06
k=2
Th 1.18 15.70 13.69 10.96
VQ 116.26 15.62 13.68 11.15
Ours 116.61 16.40 14.49 12.00
k=3
Th 1.07 15.73 13.74 11.07
VQ 55.80 15.74 13.74 11.12
Ours 53.98 16.24 14.32 11.73
Table: Results with Npairs network.
Querying val data against hash table
built on val set.
Experiments 74

95. ImageNet
Method SUF Pr@1 Pr@4 Pr@16
Npairs 1.00 15.73 13.75 11.08
k=1
Th 1.74 15.06 12.92 9.92
VQ 451.42 15.20 13.27 10.96
Ours 478.46 16.95 15.27 13.06
k=2
Th 1.18 15.70 13.69 10.96
VQ 116.26 15.62 13.68 11.15
Ours 116.61 16.40 14.49 12.00
k=3
Th 1.07 15.73 13.74 11.07
VQ 55.80 15.74 13.74 11.12
Ours 53.98 16.24 14.32 11.73
Table: Results with Npairs network.
Querying val data against hash table
built on val set.
Method SUF Pr@1 Pr@4 Pr@16
Triplet 1.00 10.90 9.39 7.45
k=1
Th 18.81 10.20 8.58 6.50
VQ 146.26 10.37 8.84 6.90
Ours 221.49 11.00 9.59 7.83
k=2
Th 6.33 10.82 9.30 7.32
VQ 32.83 10.88 9.33 7.39
Ours 60.25 11.10 9.64 7.73
k=3
Th 3.64 10.87 9.38 7.42
VQ 13.85 10.90 9.38 7.44
Ours 27.16 11.20 9.55 7.60
Table: Results with Triplet network.
Querying val data against hash table
built on val set.
Experiments 74

96. Hash table NMI
Cifar-100 ImageNet
train test val
Triplet-Th 68.20 54.95 31.62
Triplet-VQ 76.85 62.68 45.47
Triplet-Ours 89.11 68.95 48.52
Table: Hash table NMI for Cifar-100 and Imagenet.
Experiments 75

97. Hash table NMI
Cifar-100 ImageNet
train test val
Triplet-Th 68.20 54.95 31.62
Triplet-VQ 76.85 62.68 45.47
Triplet-Ours 89.11 68.95 48.52
Npairs-Th 51.46 44.32 15.20
Npairs-VQ 80.25 66.69 53.74
Npairs-Ours 84.90 68.56 55.09
Table: Hash table NMI for Cifar-100 and Imagenet.
Experiments 75

98. Outline
Background
Problem formulation
Methods
Experiments
Conclusion
Conclusion 76

99. Conclusion
We have presented a novel end-to-end optimization algorithm for
jointly learning a quantizable embedding representation and the
sparse binary hash code for efficient inference.
Conclusion 77

100. Conclusion
We have presented a novel end-to-end optimization algorithm for
jointly learning a quantizable embedding representation and the
sparse binary hash code for efficient inference.
We show an interesting connection between finding the optimal
sparse binary hash code and solving a minimum cost flow
problem.
Conclusion 77

101. Conclusion
Proposed algorithm not only achieves the state of the art search
accuracy outperforming the previous state of the art deep metric
learning approaches but also provides up to 98× and 478× search
speedup on Cifar-100 and ImageNet datasets, respectively.
Conclusion 78

102. Conclusion
Proposed algorithm not only achieves the state of the art search
accuracy outperforming the previous state of the art deep metric
learning approaches but also provides up to 98× and 478× search
speedup on Cifar-100 and ImageNet datasets, respectively.
The source code is available at
https://github.com/maestrojeong/Deep-Hash-Table-ICML18.
Conclusion 78