Convex Optimization Modelling with CVXOPTandrewmart11
An introduction to convex optimization modelling using cvxopt in an IPython environment. The facility location problem is used as an example to demonstrate modelling in cvxopt.
Basic concept of Deep Learning with explaining its structure and backpropagation method and understanding autograd in PyTorch. (+ Data parallism in PyTorch)
Introduction to Neural Networks and Deep Learning from ScratchAhmed BESBES
If you're willing to understand how neural networks work behind the scene and debug the back-propagation algorithm step by step by yourself, this presentation should be a good starting point.
We'll cover elements on:
- the popularity of neural networks and their applications
- the artificial neuron and the analogy with the biological one
- the perceptron
- the architecture of multi-layer perceptrons
- loss functions
- activation functions
- the gradient descent algorithm
At the end, there will be an implementation FROM SCRATCH of a fully functioning neural net.
code: https://github.com/ahmedbesbes/Neural-Network-from-scratch
https://telecombcn-dl.github.io/2018-dlai/
Deep learning technologies are at the core of the current revolution in artificial intelligence for multimedia data analysis. The convergence of large-scale annotated datasets and affordable GPU hardware has allowed the training of neural networks for data analysis tasks which were previously addressed with hand-crafted features. Architectures such as convolutional neural networks, recurrent neural networks or Q-nets for reinforcement learning have shaped a brand new scenario in signal processing. This course will cover the basic principles of deep learning from both an algorithmic and computational perspectives.
Convex Optimization Modelling with CVXOPTandrewmart11
An introduction to convex optimization modelling using cvxopt in an IPython environment. The facility location problem is used as an example to demonstrate modelling in cvxopt.
Basic concept of Deep Learning with explaining its structure and backpropagation method and understanding autograd in PyTorch. (+ Data parallism in PyTorch)
Introduction to Neural Networks and Deep Learning from ScratchAhmed BESBES
If you're willing to understand how neural networks work behind the scene and debug the back-propagation algorithm step by step by yourself, this presentation should be a good starting point.
We'll cover elements on:
- the popularity of neural networks and their applications
- the artificial neuron and the analogy with the biological one
- the perceptron
- the architecture of multi-layer perceptrons
- loss functions
- activation functions
- the gradient descent algorithm
At the end, there will be an implementation FROM SCRATCH of a fully functioning neural net.
code: https://github.com/ahmedbesbes/Neural-Network-from-scratch
https://telecombcn-dl.github.io/2018-dlai/
Deep learning technologies are at the core of the current revolution in artificial intelligence for multimedia data analysis. The convergence of large-scale annotated datasets and affordable GPU hardware has allowed the training of neural networks for data analysis tasks which were previously addressed with hand-crafted features. Architectures such as convolutional neural networks, recurrent neural networks or Q-nets for reinforcement learning have shaped a brand new scenario in signal processing. This course will cover the basic principles of deep learning from both an algorithmic and computational perspectives.
Abstract : For many years, Machine Learning has focused on a key issue: the design of input features to solve prediction tasks. In this presentation, we show that many learning tasks from structured output prediction to zero-shot learning can benefit from an appropriate design of output features, broadening the scope of regression. As an illustration, I will briefly review different examples and recent results obtained in my team.
This presentation was given online in July 2017 and will be given at the NY Java SIG later this year. It progressively builds on Java 8 concepts using puzzles and coding to give students confidence in their Java 8 stream/lambda skills. Handouts and code in https://github.com/boyarsky/java-8-streams-by-puzzles
Yulia Honcharenko "Application of metric learning for logo recognition"Fwdays
Typical approaches of solving classification problems require the collection of a dataset for each new class and retraining of the model. Metric learning allows you to train a model once and then easily add new classes with 5-10 reference images.
So we’ll talk about metric learning based on YouScan experience: task, data, different losses and approaches, metrics we used, pitfalls and peculiarities, things that worked and didn’t.
Gradient Boosted Regression Trees in scikit-learnDataRobot
Slides of the talk "Gradient Boosted Regression Trees in scikit-learn" by Peter Prettenhofer and Gilles Louppe held at PyData London 2014.
Abstract:
This talk describes Gradient Boosted Regression Trees (GBRT), a powerful statistical learning technique with applications in a variety of areas, ranging from web page ranking to environmental niche modeling. GBRT is a key ingredient of many winning solutions in data-mining competitions such as the Netflix Prize, the GE Flight Quest, or the Heritage Health Price.
I will give a brief introduction to the GBRT model and regression trees -- focusing on intuition rather than mathematical formulas. The majority of the talk will be dedicated to an in depth discussion how to apply GBRT in practice using scikit-learn. We will cover important topics such as regularization, model tuning and model interpretation that should significantly improve your score on Kaggle.
Paper Study: Melding the data decision pipelineChenYiHuang5
Melding the data decision pipeline: Decision-Focused Learning for Combinatorial Optimization from AAAI2019.
Derive the math equation from myself and match the same result as two mentioned CMU papers [Donti et. al. 2017, Amos et. al. 2017] while applying the same derivation procedure.
https://telecombcn-dl.github.io/2017-dlai/
Deep learning technologies are at the core of the current revolution in artificial intelligence for multimedia data analysis. The convergence of large-scale annotated datasets and affordable GPU hardware has allowed the training of neural networks for data analysis tasks which were previously addressed with hand-crafted features. Architectures such as convolutional neural networks, recurrent neural networks or Q-nets for reinforcement learning have shaped a brand new scenario in signal processing. This course will cover the basic principles of deep learning from both an algorithmic and computational perspectives.
Explore our comprehensive data analysis project presentation on predicting product ad campaign performance. Learn how data-driven insights can optimize your marketing strategies and enhance campaign effectiveness. Perfect for professionals and students looking to understand the power of data analysis in advertising. for more details visit: https://bostoninstituteofanalytics.org/data-science-and-artificial-intelligence/
Abstract : For many years, Machine Learning has focused on a key issue: the design of input features to solve prediction tasks. In this presentation, we show that many learning tasks from structured output prediction to zero-shot learning can benefit from an appropriate design of output features, broadening the scope of regression. As an illustration, I will briefly review different examples and recent results obtained in my team.
This presentation was given online in July 2017 and will be given at the NY Java SIG later this year. It progressively builds on Java 8 concepts using puzzles and coding to give students confidence in their Java 8 stream/lambda skills. Handouts and code in https://github.com/boyarsky/java-8-streams-by-puzzles
Yulia Honcharenko "Application of metric learning for logo recognition"Fwdays
Typical approaches of solving classification problems require the collection of a dataset for each new class and retraining of the model. Metric learning allows you to train a model once and then easily add new classes with 5-10 reference images.
So we’ll talk about metric learning based on YouScan experience: task, data, different losses and approaches, metrics we used, pitfalls and peculiarities, things that worked and didn’t.
Gradient Boosted Regression Trees in scikit-learnDataRobot
Slides of the talk "Gradient Boosted Regression Trees in scikit-learn" by Peter Prettenhofer and Gilles Louppe held at PyData London 2014.
Abstract:
This talk describes Gradient Boosted Regression Trees (GBRT), a powerful statistical learning technique with applications in a variety of areas, ranging from web page ranking to environmental niche modeling. GBRT is a key ingredient of many winning solutions in data-mining competitions such as the Netflix Prize, the GE Flight Quest, or the Heritage Health Price.
I will give a brief introduction to the GBRT model and regression trees -- focusing on intuition rather than mathematical formulas. The majority of the talk will be dedicated to an in depth discussion how to apply GBRT in practice using scikit-learn. We will cover important topics such as regularization, model tuning and model interpretation that should significantly improve your score on Kaggle.
Paper Study: Melding the data decision pipelineChenYiHuang5
Melding the data decision pipeline: Decision-Focused Learning for Combinatorial Optimization from AAAI2019.
Derive the math equation from myself and match the same result as two mentioned CMU papers [Donti et. al. 2017, Amos et. al. 2017] while applying the same derivation procedure.
https://telecombcn-dl.github.io/2017-dlai/
Deep learning technologies are at the core of the current revolution in artificial intelligence for multimedia data analysis. The convergence of large-scale annotated datasets and affordable GPU hardware has allowed the training of neural networks for data analysis tasks which were previously addressed with hand-crafted features. Architectures such as convolutional neural networks, recurrent neural networks or Q-nets for reinforcement learning have shaped a brand new scenario in signal processing. This course will cover the basic principles of deep learning from both an algorithmic and computational perspectives.
Explore our comprehensive data analysis project presentation on predicting product ad campaign performance. Learn how data-driven insights can optimize your marketing strategies and enhance campaign effectiveness. Perfect for professionals and students looking to understand the power of data analysis in advertising. for more details visit: https://bostoninstituteofanalytics.org/data-science-and-artificial-intelligence/
Techniques to optimize the pagerank algorithm usually fall in two categories. One is to try reducing the work per iteration, and the other is to try reducing the number of iterations. These goals are often at odds with one another. Skipping computation on vertices which have already converged has the potential to save iteration time. Skipping in-identical vertices, with the same in-links, helps reduce duplicate computations and thus could help reduce iteration time. Road networks often have chains which can be short-circuited before pagerank computation to improve performance. Final ranks of chain nodes can be easily calculated. This could reduce both the iteration time, and the number of iterations. If a graph has no dangling nodes, pagerank of each strongly connected component can be computed in topological order. This could help reduce the iteration time, no. of iterations, and also enable multi-iteration concurrency in pagerank computation. The combination of all of the above methods is the STICD algorithm. [sticd] For dynamic graphs, unchanged components whose ranks are unaffected can be skipped altogether.
StarCompliance is a leading firm specializing in the recovery of stolen cryptocurrency. Our comprehensive services are designed to assist individuals and organizations in navigating the complex process of fraud reporting, investigation, and fund recovery. We combine cutting-edge technology with expert legal support to provide a robust solution for victims of crypto theft.
Our Services Include:
Reporting to Tracking Authorities:
We immediately notify all relevant centralized exchanges (CEX), decentralized exchanges (DEX), and wallet providers about the stolen cryptocurrency. This ensures that the stolen assets are flagged as scam transactions, making it impossible for the thief to use them.
Assistance with Filing Police Reports:
We guide you through the process of filing a valid police report. Our support team provides detailed instructions on which police department to contact and helps you complete the necessary paperwork within the critical 72-hour window.
Launching the Refund Process:
Our team of experienced lawyers can initiate lawsuits on your behalf and represent you in various jurisdictions around the world. They work diligently to recover your stolen funds and ensure that justice is served.
At StarCompliance, we understand the urgency and stress involved in dealing with cryptocurrency theft. Our dedicated team works quickly and efficiently to provide you with the support and expertise needed to recover your assets. Trust us to be your partner in navigating the complexities of the crypto world and safeguarding your investments.
Adjusting primitives for graph : SHORT REPORT / NOTESSubhajit Sahu
Graph algorithms, like PageRank Compressed Sparse Row (CSR) is an adjacency-list based graph representation that is
Multiply with different modes (map)
1. Performance of sequential execution based vs OpenMP based vector multiply.
2. Comparing various launch configs for CUDA based vector multiply.
Sum with different storage types (reduce)
1. Performance of vector element sum using float vs bfloat16 as the storage type.
Sum with different modes (reduce)
1. Performance of sequential execution based vs OpenMP based vector element sum.
2. Performance of memcpy vs in-place based CUDA based vector element sum.
3. Comparing various launch configs for CUDA based vector element sum (memcpy).
4. Comparing various launch configs for CUDA based vector element sum (in-place).
Sum with in-place strategies of CUDA mode (reduce)
1. Comparing various launch configs for CUDA based vector element sum (in-place).
Opendatabay - Open Data Marketplace.pptxOpendatabay
Opendatabay.com unlocks the power of data for everyone. Open Data Marketplace fosters a collaborative hub for data enthusiasts to explore, share, and contribute to a vast collection of datasets.
First ever open hub for data enthusiasts to collaborate and innovate. A platform to explore, share, and contribute to a vast collection of datasets. Through robust quality control and innovative technologies like blockchain verification, opendatabay ensures the authenticity and reliability of datasets, empowering users to make data-driven decisions with confidence. Leverage cutting-edge AI technologies to enhance the data exploration, analysis, and discovery experience.
From intelligent search and recommendations to automated data productisation and quotation, Opendatabay AI-driven features streamline the data workflow. Finding the data you need shouldn't be a complex. Opendatabay simplifies the data acquisition process with an intuitive interface and robust search tools. Effortlessly explore, discover, and access the data you need, allowing you to focus on extracting valuable insights. Opendatabay breaks new ground with a dedicated, AI-generated, synthetic datasets.
Leverage these privacy-preserving datasets for training and testing AI models without compromising sensitive information. Opendatabay prioritizes transparency by providing detailed metadata, provenance information, and usage guidelines for each dataset, ensuring users have a comprehensive understanding of the data they're working with. By leveraging a powerful combination of distributed ledger technology and rigorous third-party audits Opendatabay ensures the authenticity and reliability of every dataset. Security is at the core of Opendatabay. Marketplace implements stringent security measures, including encryption, access controls, and regular vulnerability assessments, to safeguard your data and protect your privacy.
As Europe's leading economic powerhouse and the fourth-largest hashtag#economy globally, Germany stands at the forefront of innovation and industrial might. Renowned for its precision engineering and high-tech sectors, Germany's economic structure is heavily supported by a robust service industry, accounting for approximately 68% of its GDP. This economic clout and strategic geopolitical stance position Germany as a focal point in the global cyber threat landscape.
In the face of escalating global tensions, particularly those emanating from geopolitical disputes with nations like hashtag#Russia and hashtag#China, hashtag#Germany has witnessed a significant uptick in targeted cyber operations. Our analysis indicates a marked increase in hashtag#cyberattack sophistication aimed at critical infrastructure and key industrial sectors. These attacks range from ransomware campaigns to hashtag#AdvancedPersistentThreats (hashtag#APTs), threatening national security and business integrity.
🔑 Key findings include:
🔍 Increased frequency and complexity of cyber threats.
🔍 Escalation of state-sponsored and criminally motivated cyber operations.
🔍 Active dark web exchanges of malicious tools and tactics.
Our comprehensive report delves into these challenges, using a blend of open-source and proprietary data collection techniques. By monitoring activity on critical networks and analyzing attack patterns, our team provides a detailed overview of the threats facing German entities.
This report aims to equip stakeholders across public and private sectors with the knowledge to enhance their defensive strategies, reduce exposure to cyber risks, and reinforce Germany's resilience against cyber threats.
Chatty Kathy - UNC Bootcamp Final Project Presentation - Final Version - 5.23...John Andrews
SlideShare Description for "Chatty Kathy - UNC Bootcamp Final Project Presentation"
Title: Chatty Kathy: Enhancing Physical Activity Among Older Adults
Description:
Discover how Chatty Kathy, an innovative project developed at the UNC Bootcamp, aims to tackle the challenge of low physical activity among older adults. Our AI-driven solution uses peer interaction to boost and sustain exercise levels, significantly improving health outcomes. This presentation covers our problem statement, the rationale behind Chatty Kathy, synthetic data and persona creation, model performance metrics, a visual demonstration of the project, and potential future developments. Join us for an insightful Q&A session to explore the potential of this groundbreaking project.
Project Team: Jay Requarth, Jana Avery, John Andrews, Dr. Dick Davis II, Nee Buntoum, Nam Yeongjin & Mat Nicholas
2. www.data4sci.com
@bgoncalves
Optimization Problem
• (Machine) Learning can be thought of as an optimization problem.
• Optimization Problems have 3 distinct pieces:
• The constraints
• The function to optimize
• The optimization algorithm.
Problem Representation
Prediction Error
Gradient Descent
3. www.data4sci.com
@bgoncalves
Linear Regression
• We are assuming that our functional dependence is of the form:
• In other words, at each step, our hypothesis is:
and it imposes a Constraint on the solutions that can be found.
• We quantify our far our hypothesis is from the correct value using
an Error Function:
or, vectorially:
Sample 1
Sample 2
Sample 3
Sample 4
Sample 5
Sample 6
.
Sample M
Feature
1
Feature
3
Feature
2
…
value
Feature
N
X y
f ( ⃗
x ) = w0 + w1x1 + ⋯ + wnxn ≡ X ⃗
w
Jw (X, ⃗
y ) =
1
2m ∑
i
[hw (x(i)
) − y(i)
]
2
Jw (X, ⃗
y ) =
1
2m
[X ⃗
w − ⃗
y ]
2
hw (X) = X ⃗
w ≡ ̂
y
6. www.data4sci.com
@bgoncalves
Gradient Descent
• Goal: Find the minimum of by varying the components of
• Intuition: Follow the slope of the error function until convergence
• Algorithm:
• Guess (initial values of the parameters)
• Update until “convergence”:
Jw (X, ⃗
y ) ⃗
w
−
δ
δ ⃗
w
Jw (X, ⃗
y )
w
J
w
(
X,
⃗
y
)
⃗
w(0)
wj = wj − α
δ
δwj
Jw (X, ⃗
y )
J
w
(
X
,
⃗
y
)
−
δ
δ ⃗
w
Jw (X, ⃗
y )
step size
δ
δwj
Jw (X, ⃗
y ) =
1
m
XT
⋅ (hw (X) − ⃗
y )
7. www.data4sci.com
@bgoncalves
`
0
3.25
6.5
9.75
13
0 5 10 15 20
2D
Geometric Interpretation
y = w0 + w1x1
3D
y = w0 + w1x1 + w2x2
nD
y = X ⃗
w
Add
to account
for intercept
x0 ≡ 1
Finds the hyperplane that
splits the points in two
such that the errors on
each side balance out
8. Code - Linear Regression
https://github.com/DataForScience/DeepLearning
12. @bgoncalves
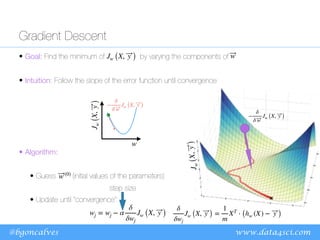
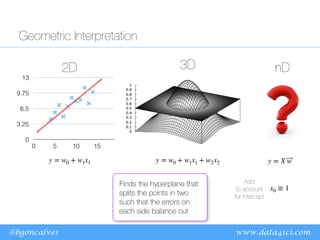
Logistic Regression (Classification)
• Not actually regression, but rather Classification
• Predict the probability of instance belonging to the given class:
• Use sigmoid/logistic function to map weighted inputs to
hw (X) ∈ [0,1]
hw (X) = ϕ (X ⃗
w)
[0,1]
z encapsulates all
the parameters and
input values
1 - part of the class
0 - otherwise
14. www.data4sci.com
@bgoncalves
Logistic Regression
• Error Function - Cross Entropy
measures the “distance” between two probability distributions
• Effectively treating the labels as probabilities (an instance with label=1 has Probability 1 of
belonging to the class).
• Gradient - same as Logistic Regression
Jw (X, ⃗
y ) = −
1
m [yT
log (hw (X)) + (1 − y)
T
log (1 − hw (X))]
hw (X) =
1
1 + e−X ⃗
w
wj = wj − α
δ
δwj
Jw (X, ⃗
y )
δ
δwj
Jw (X, ⃗
y ) =
1
m
XT
⋅ (hw (X) − ⃗
y )
25. www.data4sci.com
@bgoncalves
Activation Function - Linear
• Non-Linear function
• Differentiable
• non-decreasing
• Compute new sets of features
• Each layer builds up a more abstract
representation of the data
• The simplest
ϕ (z) = z
26. www.data4sci.com
@bgoncalves
Activation Function - Linear
• Non-Linear function
• Differentiable
• non-decreasing
• Compute new sets of features
• Each layer builds up a more abstract
representation of the data
• The simplest
Linear Regression
ϕ (z) = z
27. www.data4sci.com
@bgoncalves
Activation Function - Sigmoid
• Non-Linear function
• Differentiable
• non-decreasing
• Compute new sets of features
• Each layer builds up a more abstract
representation of the data
• Perhaps the most common
ϕ (z) =
1
1 + e−z
28. www.data4sci.com
@bgoncalves
Activation Function - Sigmoid
• Non-Linear function
• Differentiable
• non-decreasing
• Compute new sets of features
• Each layer builds up a more abstract
representation of the data
• Perhaps the most common
ϕ (z) =
1
1 + e−z
Logistic Regression
29. www.data4sci.com
@bgoncalves
Forward Propagation
• The output of a perceptron is determined by a sequence of steps:
• obtain the inputs
• multiply the inputs by the respective weights
• calculate output using the activation function
31. www.data4sci.com
@bgoncalves
Activation Function - ReLu
• Non-Linear function
• Differentiable
• non-decreasing
• Compute new sets of features
• Each layer builds up a more abstract
representation of the data
• Results in faster learning than with
sigmoid
ϕ (z) = z, z > 0
32. www.data4sci.com
@bgoncalves
ϕ (z) = z, z > 0
Activation Function - ReLu
• Non-Linear function
• Differentiable
• non-decreasing
• Compute new sets of features
• Each layer builds up a more abstract
representation of the data
• Results in faster learning than with
sigmoid
Stepwise Regression
33. www.data4sci.com
@bgoncalves
Stepwise Regression
• Multivariate Adaptive Regression Spline (MARS) is the best known example
• Fit curves using a linear combination of:
• The basis functions can be:
• Constant
• “Hinge” functions of the form: and
• Products of hinges
https://en.wikipedia.org/wiki/Multivariate_adaptive_regression_spline
max(0, x − b) max(0, b − x)
̂
f (x) =
∑
i
ciBi (x)
Bi (x)
34. www.data4sci.com
@bgoncalves
Stepwise Regression
• Multivariate Adaptive Regression Spline (MARS) is the best known example
• Fit curves using a linear combination of:
https://en.wikipedia.org/wiki/Multivariate_adaptive_regression_spline
y (x) = 1.013
+ 1.198 max (0, x 0.485)
1.803 max (0, 0.485 x)
1.321 max (0, x 0.283)
1.609 max (0, x 0.640)
+ 1.591 max (0, x 0.907)
<latexit sha1_base64="8sdMuX6MlC9h4jWMaRP7SJkiDEU=">AAAC9XicbZLPb9MwFMedjB8jA9axIxeLimr8WGS3+5EekCZx4Tgkuk1qqspxndaa4wTbYY2i7u/gwgGEuPK/cOO/wWlzKFmfZOmr9z7v+b1nR5ng2iD013G37t1/8HD7kbfz+MnT3dbeswud5oqyAU1Fqq4iopngkg0MN4JdZYqRJBLsMrp+X8UvvzCleSo/mSJjo4RMJY85Jca6xnvOThixKZcl+yyJUqR4vfCKULDYHMxDxacz86rzroN9hHth6HXeWIn7AbyFCZmvMPQWzuEhRP5RcFxnVOShJQPUa5BLytLzBtnr4o01u0GvQZ6g/kby5AitkVWfx/3NNfvotCa9kMnJ2uTjVhv5aGnwrsC1aIPazsetP+EkpXnCpKGCaD3EKDOjkijDqWALL8w1ywi9JlM2tFKShOlRuXy1BXxpPRMYp8oeaeDSu55RkkTrIoksmRAz081Y5dwUG+YmDkYll1lumKSri+JcQJPC6gvACVeMGlFYQajitldIZ0QRauxH8ewScHPku+Ki62Pk44/d9llQr2MbPAcvwAHA4BScgQ/gHAwAdZTz1fnu/HBv3G/uT/fXCnWdOmcf/Gfu739e5dqD</latexit>
<latexit sha1_base64="8sdMuX6MlC9h4jWMaRP7SJkiDEU=">AAAC9XicbZLPb9MwFMedjB8jA9axIxeLimr8WGS3+5EekCZx4Tgkuk1qqspxndaa4wTbYY2i7u/gwgGEuPK/cOO/wWlzKFmfZOmr9z7v+b1nR5ng2iD013G37t1/8HD7kbfz+MnT3dbeswud5oqyAU1Fqq4iopngkg0MN4JdZYqRJBLsMrp+X8UvvzCleSo/mSJjo4RMJY85Jca6xnvOThixKZcl+yyJUqR4vfCKULDYHMxDxacz86rzroN9hHth6HXeWIn7AbyFCZmvMPQWzuEhRP5RcFxnVOShJQPUa5BLytLzBtnr4o01u0GvQZ6g/kby5AitkVWfx/3NNfvotCa9kMnJ2uTjVhv5aGnwrsC1aIPazsetP+EkpXnCpKGCaD3EKDOjkijDqWALL8w1ywi9JlM2tFKShOlRuXy1BXxpPRMYp8oeaeDSu55RkkTrIoksmRAz081Y5dwUG+YmDkYll1lumKSri+JcQJPC6gvACVeMGlFYQajitldIZ0QRauxH8ewScHPku+Ki62Pk44/d9llQr2MbPAcvwAHA4BScgQ/gHAwAdZTz1fnu/HBv3G/uT/fXCnWdOmcf/Gfu739e5dqD</latexit>
<latexit sha1_base64="8sdMuX6MlC9h4jWMaRP7SJkiDEU=">AAAC9XicbZLPb9MwFMedjB8jA9axIxeLimr8WGS3+5EekCZx4Tgkuk1qqspxndaa4wTbYY2i7u/gwgGEuPK/cOO/wWlzKFmfZOmr9z7v+b1nR5ng2iD013G37t1/8HD7kbfz+MnT3dbeswud5oqyAU1Fqq4iopngkg0MN4JdZYqRJBLsMrp+X8UvvzCleSo/mSJjo4RMJY85Jca6xnvOThixKZcl+yyJUqR4vfCKULDYHMxDxacz86rzroN9hHth6HXeWIn7AbyFCZmvMPQWzuEhRP5RcFxnVOShJQPUa5BLytLzBtnr4o01u0GvQZ6g/kby5AitkVWfx/3NNfvotCa9kMnJ2uTjVhv5aGnwrsC1aIPazsetP+EkpXnCpKGCaD3EKDOjkijDqWALL8w1ywi9JlM2tFKShOlRuXy1BXxpPRMYp8oeaeDSu55RkkTrIoksmRAz081Y5dwUG+YmDkYll1lumKSri+JcQJPC6gvACVeMGlFYQajitldIZ0QRauxH8ewScHPku+Ki62Pk44/d9llQr2MbPAcvwAHA4BScgQ/gHAwAdZTz1fnu/HBv3G/uT/fXCnWdOmcf/Gfu739e5dqD</latexit>
<latexit sha1_base64="8sdMuX6MlC9h4jWMaRP7SJkiDEU=">AAAC9XicbZLPb9MwFMedjB8jA9axIxeLimr8WGS3+5EekCZx4Tgkuk1qqspxndaa4wTbYY2i7u/gwgGEuPK/cOO/wWlzKFmfZOmr9z7v+b1nR5ng2iD013G37t1/8HD7kbfz+MnT3dbeswud5oqyAU1Fqq4iopngkg0MN4JdZYqRJBLsMrp+X8UvvzCleSo/mSJjo4RMJY85Jca6xnvOThixKZcl+yyJUqR4vfCKULDYHMxDxacz86rzroN9hHth6HXeWIn7AbyFCZmvMPQWzuEhRP5RcFxnVOShJQPUa5BLytLzBtnr4o01u0GvQZ6g/kby5AitkVWfx/3NNfvotCa9kMnJ2uTjVhv5aGnwrsC1aIPazsetP+EkpXnCpKGCaD3EKDOjkijDqWALL8w1ywi9JlM2tFKShOlRuXy1BXxpPRMYp8oeaeDSu55RkkTrIoksmRAz081Y5dwUG+YmDkYll1lumKSri+JcQJPC6gvACVeMGlFYQajitldIZ0QRauxH8ewScHPku+Ki62Pk44/d9llQr2MbPAcvwAHA4BScgQ/gHAwAdZTz1fnu/HBv3G/uT/fXCnWdOmcf/Gfu739e5dqD</latexit>
̂
f (x) =
∑
i
ciBi (x)
35. www.data4sci.com
@bgoncalves
Forward Propagation
• The output of a perceptron is determined by a sequence of steps:
• obtain the inputs
• multiply the inputs by the respective weights
• calculate output using the activation function
• To create a multi-layer perceptron, you can simply use the output of one layer as the input to
the next one.
• But how can we propagate back the errors and update the weights?
x1
x2
x3
xN
w
1j
w2j
w3j
wN
j
aj
w
0j
1
wT
x
1
w
0k
w
1k
w2k
w3k
wNk
ak
wT
a
a1
a2
aN
36. www.data4sci.com
@bgoncalves
Stepwise Regression https://en.wikipedia.org/wiki/Multivariate_adaptive_regression_spline
̂
f (x) =
∑
i
ciBi (x)
y (x) = 1.013
+ 1.198 max (0, x 0.485)
1.803 max (0, 0.485 x)
1.321 max (0, x 0.283)
1.609 max (0, x 0.640)
+ 1.591 max (0, x 0.907)
<latexit sha1_base64="8sdMuX6MlC9h4jWMaRP7SJkiDEU=">AAAC9XicbZLPb9MwFMedjB8jA9axIxeLimr8WGS3+5EekCZx4Tgkuk1qqspxndaa4wTbYY2i7u/gwgGEuPK/cOO/wWlzKFmfZOmr9z7v+b1nR5ng2iD013G37t1/8HD7kbfz+MnT3dbeswud5oqyAU1Fqq4iopngkg0MN4JdZYqRJBLsMrp+X8UvvzCleSo/mSJjo4RMJY85Jca6xnvOThixKZcl+yyJUqR4vfCKULDYHMxDxacz86rzroN9hHth6HXeWIn7AbyFCZmvMPQWzuEhRP5RcFxnVOShJQPUa5BLytLzBtnr4o01u0GvQZ6g/kby5AitkVWfx/3NNfvotCa9kMnJ2uTjVhv5aGnwrsC1aIPazsetP+EkpXnCpKGCaD3EKDOjkijDqWALL8w1ywi9JlM2tFKShOlRuXy1BXxpPRMYp8oeaeDSu55RkkTrIoksmRAz081Y5dwUG+YmDkYll1lumKSri+JcQJPC6gvACVeMGlFYQajitldIZ0QRauxH8ewScHPku+Ki62Pk44/d9llQr2MbPAcvwAHA4BScgQ/gHAwAdZTz1fnu/HBv3G/uT/fXCnWdOmcf/Gfu739e5dqD</latexit>
<latexit sha1_base64="8sdMuX6MlC9h4jWMaRP7SJkiDEU=">AAAC9XicbZLPb9MwFMedjB8jA9axIxeLimr8WGS3+5EekCZx4Tgkuk1qqspxndaa4wTbYY2i7u/gwgGEuPK/cOO/wWlzKFmfZOmr9z7v+b1nR5ng2iD013G37t1/8HD7kbfz+MnT3dbeswud5oqyAU1Fqq4iopngkg0MN4JdZYqRJBLsMrp+X8UvvzCleSo/mSJjo4RMJY85Jca6xnvOThixKZcl+yyJUqR4vfCKULDYHMxDxacz86rzroN9hHth6HXeWIn7AbyFCZmvMPQWzuEhRP5RcFxnVOShJQPUa5BLytLzBtnr4o01u0GvQZ6g/kby5AitkVWfx/3NNfvotCa9kMnJ2uTjVhv5aGnwrsC1aIPazsetP+EkpXnCpKGCaD3EKDOjkijDqWALL8w1ywi9JlM2tFKShOlRuXy1BXxpPRMYp8oeaeDSu55RkkTrIoksmRAz081Y5dwUG+YmDkYll1lumKSri+JcQJPC6gvACVeMGlFYQajitldIZ0QRauxH8ewScHPku+Ki62Pk44/d9llQr2MbPAcvwAHA4BScgQ/gHAwAdZTz1fnu/HBv3G/uT/fXCnWdOmcf/Gfu739e5dqD</latexit>
<latexit sha1_base64="8sdMuX6MlC9h4jWMaRP7SJkiDEU=">AAAC9XicbZLPb9MwFMedjB8jA9axIxeLimr8WGS3+5EekCZx4Tgkuk1qqspxndaa4wTbYY2i7u/gwgGEuPK/cOO/wWlzKFmfZOmr9z7v+b1nR5ng2iD013G37t1/8HD7kbfz+MnT3dbeswud5oqyAU1Fqq4iopngkg0MN4JdZYqRJBLsMrp+X8UvvzCleSo/mSJjo4RMJY85Jca6xnvOThixKZcl+yyJUqR4vfCKULDYHMxDxacz86rzroN9hHth6HXeWIn7AbyFCZmvMPQWzuEhRP5RcFxnVOShJQPUa5BLytLzBtnr4o01u0GvQZ6g/kby5AitkVWfx/3NNfvotCa9kMnJ2uTjVhv5aGnwrsC1aIPazsetP+EkpXnCpKGCaD3EKDOjkijDqWALL8w1ywi9JlM2tFKShOlRuXy1BXxpPRMYp8oeaeDSu55RkkTrIoksmRAz081Y5dwUG+YmDkYll1lumKSri+JcQJPC6gvACVeMGlFYQajitldIZ0QRauxH8ewScHPku+Ki62Pk44/d9llQr2MbPAcvwAHA4BScgQ/gHAwAdZTz1fnu/HBv3G/uT/fXCnWdOmcf/Gfu739e5dqD</latexit>
<latexit sha1_base64="8sdMuX6MlC9h4jWMaRP7SJkiDEU=">AAAC9XicbZLPb9MwFMedjB8jA9axIxeLimr8WGS3+5EekCZx4Tgkuk1qqspxndaa4wTbYY2i7u/gwgGEuPK/cOO/wWlzKFmfZOmr9z7v+b1nR5ng2iD013G37t1/8HD7kbfz+MnT3dbeswud5oqyAU1Fqq4iopngkg0MN4JdZYqRJBLsMrp+X8UvvzCleSo/mSJjo4RMJY85Jca6xnvOThixKZcl+yyJUqR4vfCKULDYHMxDxacz86rzroN9hHth6HXeWIn7AbyFCZmvMPQWzuEhRP5RcFxnVOShJQPUa5BLytLzBtnr4o01u0GvQZ6g/kby5AitkVWfx/3NNfvotCa9kMnJ2uTjVhv5aGnwrsC1aIPazsetP+EkpXnCpKGCaD3EKDOjkijDqWALL8w1ywi9JlM2tFKShOlRuXy1BXxpPRMYp8oeaeDSu55RkkTrIoksmRAz081Y5dwUG+YmDkYll1lumKSri+JcQJPC6gvACVeMGlFYQajitldIZ0QRauxH8ewScHPku+Ki62Pk44/d9llQr2MbPAcvwAHA4BScgQ/gHAwAdZTz1fnu/HBv3G/uT/fXCnWdOmcf/Gfu739e5dqD</latexit>
ReLu
1
x
ReLu
1
x
ReLu
1
x
Linear
1
37. www.data4sci.com
@bgoncalves
The Cross Entropy is complementary to sigmoid
activation in the output layer and improves its stability.
Loss Functions
• For learning to occur, we must quantify how far off we are from the desired output. There are
two common ways of doing this:
• Quadratic error function:
• Cross Entropy
E =
1
N
X
n
|yn an|
2
J =
1
N
X
n
h
yT
n log an + (1 yn)
T
log (1 an)
i
38. www.data4sci.com
@bgoncalves
Regularization
• Helps keep weights relatively small by adding a penalization to the cost function.
• Two common choices:
• Lasso helps with feature selection by driving less important weights to zero
̂
Jw (X) = Jw (X) + λ
∑
ij
w2
ij
̂
Jw (X) = Jw (X) + λ
∑
ij
wij “Lasso”
L2
39. www.data4sci.com
@bgoncalves
Backward Propagation of Errors (BackProp)
• BackProp operates in two phases:
• Forward propagate the inputs and calculate the deltas
• Update the weights
• The error at the output is a weighted average difference between predicted output and the
observed one.
• For inner layers there is no “real output”!
40. www.data4sci.com
@bgoncalves
• Let be the error at each of the total layers:
• Then:
• And for every other layer, in reverse order:
• Until:
as there’s no error on the input layer.
• And finally:
BackProp
δ(l)
δ(L)
= hw (X) − y
δ(l)
= W(l)T
δ(l+1)
. * ϕ†
(z(l)
)
L
δ(1)
≡ 0
Δ(l)
ij
= Δ(l)
ij
+ a(l)
j
δ(l+1)
i
∂
∂w(l)
ij
Jw (X, ⃗
y ) =
1
m
Δ(l)
ij
+ λw(l)
ij
41. @bgoncalves
A practical example - MNIST
8
2
Sample 1
Sample 2
Sample 3
Sample 4
Sample 5
Sample 6
.
Sample N
Feature
1
Feature
3
Feature
2
…
Label
Feature
M
yann.lecun.com/exdb/mnist/
42. @bgoncalves
A practical example - MNIST
yann.lecun.com/exdb/mnist/
Sample 1
Sample 2
Sample 3
Sample 4
Sample 5
Sample 6
.
Sample M
Feature
1
Feature
3
Feature
2
…
Label
Feature
N
X y
3 layers:
1 input layer
1 hidden layer
1 output layer
X ⇥1 ⇥2
arg
max
43. www.data4sci.com
@bgoncalves
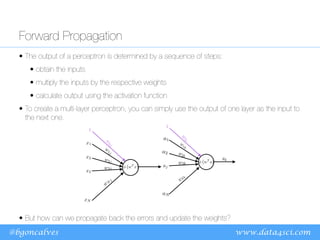
A practical example - MNIST
784 50 10 1
5000
examples
10 ⇥ 51
50 ⇥ 785
def predict(Theta1, Theta2, X):
h1 = forward(Theta1, X, sigmoid)
h2 = forward(Theta2, h1, sigmoid)
return np.argmax(h2, 1)
50 ⇥ 784 10 ⇥ 50
Forward Propagation
Backward Propagation
Vectors
Matrices
Matrices
X ⇥1 ⇥2
arg
max
def forward(Theta, X, active):
N = X.shape[0]
# Add the bias column
X_ = np.concatenate((np.ones((N, 1)), X), 1)
# Multiply by the weights
z = np.dot(X_, Theta.T)
# Apply the activation function
a = active(z)
return a
