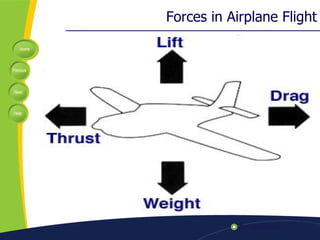
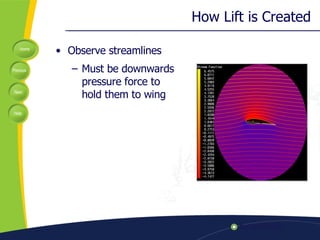
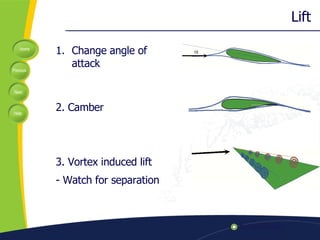
The document discusses key factors in subsonic airplane design, including lift, weight, thrust, drag, center of mass, and center of pressure. It examines ratios like the Mach number and Reynolds number that are important for interpretation. Design considerations like wing design, induced drag, and stalling velocity are covered. A case study of the Helios aircraft is presented, which set an unofficial altitude record of 96,863 feet in 2001 but later crashed during a test flight.

1. Subsonic Airplane Design Christopher Weyant Joseph Rebolledo COSMOS at UC Davis Cluster 3 August 3, 2006

2. Presentation Outline Main factors that allow flight Ratios to interpret these factors Important design considerations Case study- Helios

3. I. Factors that Allow Airplane Flight Lift Weight Thrust Drag Center of mass Center of pressure

4. Forces in Airplane Flight

5. How Lift is Created Observe streamlines Must be downwards pressure force to hold them to wing

6. How Lift is Created Imagine boxes stacked above and below wing Top of box must have higher pressure than bottom Lower pressure on top of wing than bottom Pressure gradient causes lift high pressure low pressure= next high pressure low pressure pressure force pressure force

7. Lift Three main ways to increase lift: Increase angle of attack Camber Vortex-Induced Lift

8. Lift Change angle of attack 2. Camber 3. Vortex induced lift - Watch for separation

9. Weight Weight measures the downward gravitational pull on the aircraft Several components contribute to the weight of an aircraft: Physical plane Fuel Payload

10. Weight Considerations Lift must exceed weight to take off In obtaining lift, drag must be less than thrust to accelerate and take off

11. How Thrust is Created Propulsive device exerts force on air Equal and opposite force exerted back on plane Makes plane go forward and overcome drag

12. Thrust Pressure and sheer stress distribution on surface area cause thrust Thrust equation T=ṁ(V ∞ - V j ) T; thrust [newtons; kgm/s 2 ] ṁ; mass flow through device [kg/s] V ∞ ; velocity of air leaving plane [m/s] V j ; velocity of air ahead of plane [m/s]

13. Thrust Total power generated by propulsive device = TV ∞ +1/2ṁ(V j -V ∞ ) 2 (power available) + (wasted/ KE)

14. Thrust vs. Efficiency Useful power ( η p ) = 2/(1+V j /V ∞ ) 100% efficiency has V j = V ∞ However, then no thrust Tradeoff

15. How Drag is Created Friction drag Drag due to friction over surface Pressure drag Inequality of surface pressure that causes drag Induced drag Pressure drag associated with wing tip vortices

16. Center of Pressure Sum pressure forces into a single force Point through which lift and drag act Also, the point at which there is no moment To find, plot distributed load and find centroid

17. Center of Mass Average location of weight Balance object on that point Point from which gravity can be drawn To find, cg = ( ∫ [x * w(x)]dx) / ( ∫ [w(x)]dx) Sum of weights of slices times distances to nose divided by the sum of the weights; weighted average x= distance from nose tip of aircraft back to slice [m] dx= small slices perpendicular to x [m] w(x)= weight of slice contained in dx; newton [kgm/s 2 ] Assume weight is distributed symmetrically around center line

18. Centers of Mass and Pressure Center of pressure is behind center of mass Leads to increased stability by correcting for angle of attack Horizontal stabilizer provides downwards force Wing provides upwards lift When angle of attack increases, wing lift increase and horizontal stabilizer rotates nose back down They must be on same line, so as to not create torque along the yaw or roll axes

19. II. Useful Non-dimensional Ratios Mach number Reynolds number Aspect ratio Coefficient of lift Coefficient of drag

20. Mach Number Compressibility effects Ma= speed airplane/ speed sound= V/a Ma<1; subsonic Ma≈1; transonic Ma>1; supersonic Ma>>1; hypersonic Ma 2 =-( Δρ / ρ )/( Δ V/V) = change in density/change in velocity

21. Reynolds number Viscosity effects Re= ρ ∞ v ∞ c/ μ ∞ pressure vs. viscosity ρ ∞ = free stream air density [kg/m 3 ] V ∞ = free stream air velocity [m/s] c= chord length [m] μ ∞ = ambient coefficient of viscosity; [Kg/ms] Less than 2300 is laminar Over 2300 is turbulent

22. Aspect Ratio Three dimensional effects Tells how skinny wing is AR= b 2 /S b= wingspan [m] S= planform area of wing [m 2 ]

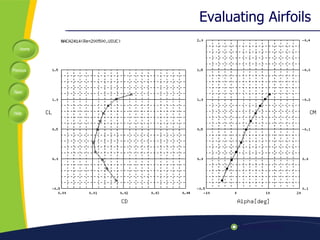
23. Coefficient of Lift C L = L/( ½ ρ V 2 S) C L =coefficient of lift [dimensionless] L= lift; newton [kgm/s 2 ] ρ = air density [kg/m 3 ] V= velocity; [m/s] S= planform wing area [m 2 ]

24. Coefficient of Drag C D = D/( ½ ρ V 2 S) C D =coefficient of drag [dimensionless] D= drag; newton [kgm/s 2 ] ρ = air density [kg/m 3 ] V= velocity [m/s] S= planform wing area [m 2 ]

25. III. Design of Subsonic Airplanes Stalling velocity Wing design Induced drag Angle of attack Ceiling altitude Evaluating airfoils

26. Stalling Velocity V stall = √(2/ ρ ∞ )(W/S)(1/C L max ) V stall = stalling velocity [m/s] ρ ∞ = free stream air density [ kg/m 3 ] W= weight; newtons [ kgm/s 2 ] S= planform surface area of wing [m 2 ] C L max = maximum lift coefficient [dimensionless]

27. Implications Gets larger at higher altitudes, due to decreasing air density Increases with weight Decreases with planform wing area Decreases with higher C L max

28. Different Types of Wings High aspect- ratio straight wing Low aspect- ratio straight wing Swept wing Delta wing Simple delta Cropped delta Notched delta Double delta

29. Prandtl’s Lifting Line Theory a=a o /(1+(a o /  e 1 AR) a= lift slope for finite wing [per radian] a 0 = lift slope for infinite wing [per radian] e 1 = ratio of tip chord to root chord [dimensionless] AR= b 2 /S [dimensionless]

30. Implications Lift slope decreases with aspect ratio Straight wing to maximize e 1 Experimentally, C L max decreases with aspect ratio

31. Prandtl- Glauert Rule a o,comp = a 0 / √1 - M ∞ 2 a o = incompressible lift slope [per radian] M ∞ = free stream mach number [dimensionless]

32. Combined a comp = a o / √1-M ∞ +a o /(  e 1 AR) a o = incompressible lift slope [per radian] a comp = compressible lift slope [per radian] M ∞ = free stream mach number [dimensionless] e 1 = ratio of tip chord to root chord [dimensionless] AR= b 2 /S [dimensionless] Works well for .3<Ma<.7

33. Implications Same as before, but modified to account for compressible flows Lift slope decreases with aspect ratio Straight wing to maximize e 1 Experimentally, C L max decreases with aspect ratio

34. Equation for Induced Drag C Di = (C L 2 )/(  (AR)e) Where: C L ; coefficient of lift [dimensionless] AR; aspect ratio [dimensionless] e; spanwise efficiency factor, how C Di for wing relates to ideal wing with the same aspect ratio [dimensionless]

35. Implications Biggest source of drag for low speed aircraft Wings with the largest possible aspect ratio For low speed aircraft, aspect ratios as high as 15 or more are used

36. Angle of Attack Angle that wing is inclined to flow Want only small angle of attack needed to achieve adequate lift at low speed Can be built into wing through camber

37. Ceiling Altitude ( R/C) max = maximum rate of climb [m/sec] η pr = propeller efficiency; power available/ shaft power [dimensionless] P= power [W] W= weight newtons [ kgm/s 2 ] ρ ∞ = free stream air density [kg/m 3 ] K= Coefficient of Cl 2 in drag polar [dimensionless] C D.O= Zero lift drag coefficient [dimensionless] S= planform surface area of wing [m 2 ] L/D max = maximum lift to drag ratio [dimensionless] (R/C) max =( η pr P/W)–[(2/ ρ ∞ )√K/3C D.0 (W/S)] 1/2 *(1.55/(L/D max ))

38. Implications η pr P/W want big Bigger engine, more efficient propeller, less weight K wants smaller Higher aspect ratio W/S want small - Less weight - Larger surface area of wing L/D max want big Less drag More lift

39. Limits on Reducing Drag Aspect ratio and surface area have to be within a range Makes aircraft heavier which requires more lift Increases skin friction drag which requires more power If aspect ratio is too high, loose stability

40. Evaluating Airfoils

41. Explanation For these graphs, Re= 200,500 First graph shows C D and C L of airfoil Want high C L for given C D Second shows  and  C L Want high C L for given  Third shows  and CM Want low CM for given 

42. Coffin Corner Problem faced by high altitude low speed flight If slow down at high altitude, stall If speed up, break sound barrier and generate too much drag and stall

43. IV. Case Study- Helios Part of HALE $103 million from NASA $36 million from industry

44. Goals for Helios Reach 100,000 ft. Have non-stop flight for 24 hours, and to have at least 14 hours above 50,000 ft.

45. Significance of Helios Study atmospheric science Observe the Earth Serve as telecommunication system

46. Helios Aircraft Statistics Wing span of 247 ft Length of 12 ft Wing chord of 8 ft Wing area is 1,976 sq ft Aspect ratio of 31 to 1 Gross weight is 1,600 lb Payload of 726 lbs Airspeed of 19 to 27 mph Up to 170 mph at altitude 72 trailing edge elevators

47. Helios Propulsion Statistics 14 brushless DC electric motors, 1.5 kW each 62,000 solar cells Endurance of several days to several months

48. Helios Accomplishes a Goal (2001) Unofficial altitude record of 96,863 ft Stayed over 96,000 ft for over 40 min Did not meet flight endurance goal Scientists worked on for 2003 flight

49. Helios Malfunctions 3,000 ft. up in restricted Navy airspace Control difficulties Severe oscillations occurred Structural damage lead to crash No environmental effect, but plane lost 75 percent by weight recovered

50. Summary Main factors that allow flight Ratios to interpret these factors Important design considerations Case study- Helios

51. Acknowledgements Professor Hafez Professor Horsley Michael Paskowitz Margarita Montes Tim McGuire Taylor Roche Beth Kuspa

52. Bibliography www.nasa.gov Aircraft Performance and Design by John D. Anderson, Jr. http://www.nasg.com/afdb/list-polar-e.phtml http://www.aa.nps.navy.mil/~jones/research/gui/joukowski/sample_results/