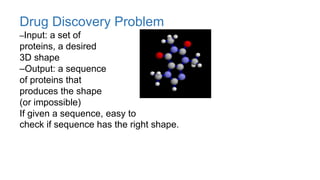
The document discusses the subset sum problem and approaches to solve it. It begins by defining the problem and providing an example. It then analyzes the brute force approach of checking all possible subsets and calculates its exponential time complexity. The document introduces dynamic programming as an efficient alternative, providing pseudocode for a dynamic programming algorithm that solves the problem in polynomial time by storing previously computed solutions. It concludes by discussing applications of similar problems in traveling salesperson and drug discovery.

1. Willing is not enough, we must do
Bruce lee

2. Problem Statement:
In the subset-sum problem, we are given a finite set S of positive
integers and an integer target t > 0. We ask whether there exists a
subset S`⊆ S whose elements sum to t.

3. TRUE FALSE
t = 138457 TRUE
How to Design an Algorithm to Solve this Problem??

4. Brute Force??
Making all possible Subsets

5. A={1,2,4}
What will be its Complexity???
All possible subsets???
1. A’={}
2. A’={1}
3. A’={1,2}
4. A’={1,4}
5. A’={1,2,4}
6. A’={2}
7. A’={2,4}
8. A’={4}
SumOFSubset=2n=8

6. Brute Force Subset Sum Solution
Running time Q(n 2n )
What does this tell us about the time
complexity of the subset sum problem?
bool SumSub (w, i, j)
{
if (i == 0) return (j == 0);
else
if (SumSub (w, i-1, j)) return true;
else if ((j - wi) >= 0) return SumSub (w, i-1, j - wi);
else return false;
}

7. Complexity
0( 2n N)
All possible subsets and time required to sum them.
Brute Force??? No, thanks
Why is this Failing???

8. • Sometimes, the divide and conquer
approach seems appropriate but fails
to produce an efficient algorithm.
• One of the reasons is that D&Q
produces overlapping sub problems.

9. Dynamic Approach
Divide and conquer with Tabular form
Solves a sub-problem by making use of previously stored
solutions for all other sub problems.
HOW?????

10. Lets take an example
0 1 2 3 4 5 6 7 8 9 10 11
2
3
7
8
10
A={2,3,7,8,10} t=11
Any subset of { 2} making sum=0 ???

11. Lets take an example
0 1 2 3 4 5 6 7 8 9 10 11
2 T
3
7
8
10
A={2,3,7,8,10} t=11

12. Lets take an example
0 1 2 3 4 5 6 7 8 9 10 11
2 T F
3
7
8
10
A={2,3,7,8,10} t=11
Any subset of { 2} making sum=1 ???

13. Lets take an example
0 1 2 3 4 5 6 7 8 9 10 11
2 T F T
3
7
8
10
A={2,3,7,8,10} t=11
Any subset of { 2} making sum=3 ???

14. Lets take an example
0 1 2 3 4 5 6 7 8 9 10 11
2 T F T F F F F F F F F F
3 T F T T F T F F F F F F
7 T F T T F T F T F T T F
8 T F T T F T F T T T T T
10 T F T T F T F T T T T T
A={2,3,7,8,10} t=11
How to get the Answer??

15. 8 is one of the Element

16. 3 is one of the Element

17. As we have reached the Last row..
A’={8,3} is our Answer 

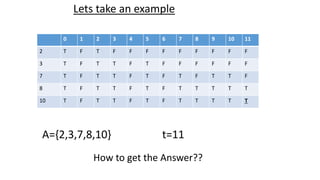
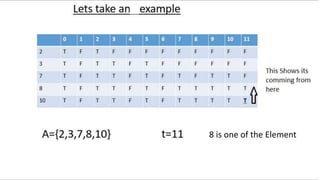
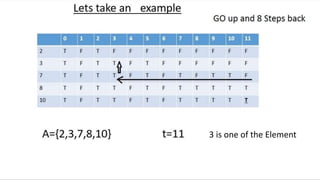
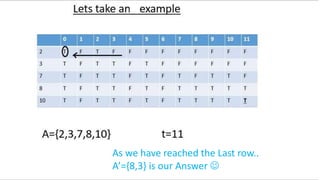
18. 18
Dynamic Programming Algorithm
bool SumSub (w , n , m)
{
1. t[0,0] = true; for (j = 1 to m) t[0,j] = false;
2. for (i = 1 to n)
3. for (j = 0 to m)
4. t[i,j] = t[i-1,j];
5. if ((j-wi) >= 0)
6. t[i,j] = t[i-1,j] || t[i-1, j – wi];
7. return t[n,m];
}
i-1,
j - wi
i-1,
j
i , j
Its Complexity???
Time complexity is T(n) = O(m) + O(nm) = O(nm)

19. Application
Traveling Salesperson Problem
–Input: a graph of cities and roads
with distance connecting them and a
minimum total distant
–Output: either a path that visits each
with a cost less than the minimum,
or “no”.
• If given a path, easy to check if it
visits every city with less than
minimum distance travelled.

20. Drug Discovery Problem
–Input: a set of
proteins, a desired
3D shape
–Output: a sequence
of proteins that
produces the shape
(or impossible)
If given a sequence, easy to
check if sequence has the right shape.

21. THE END