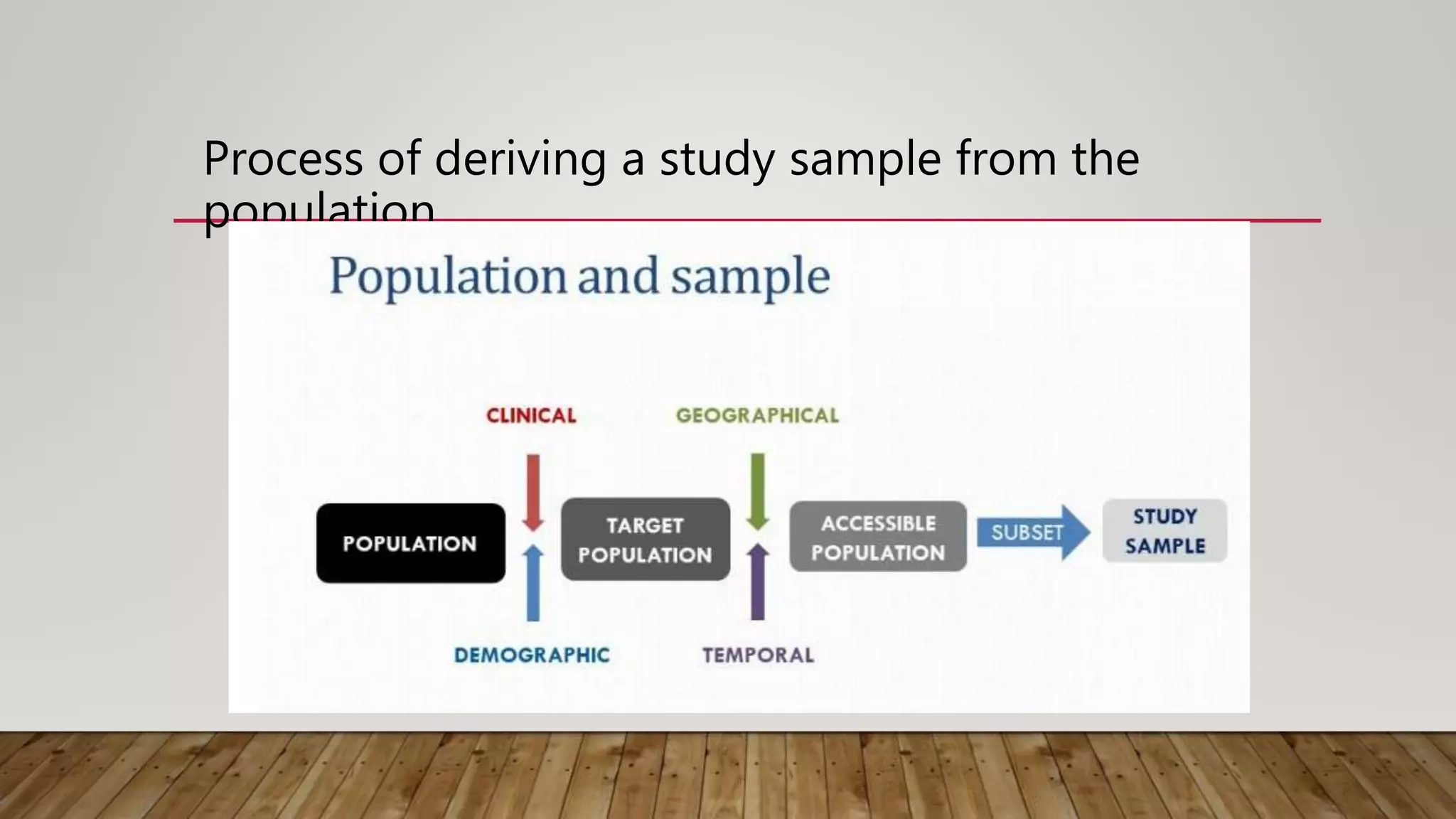
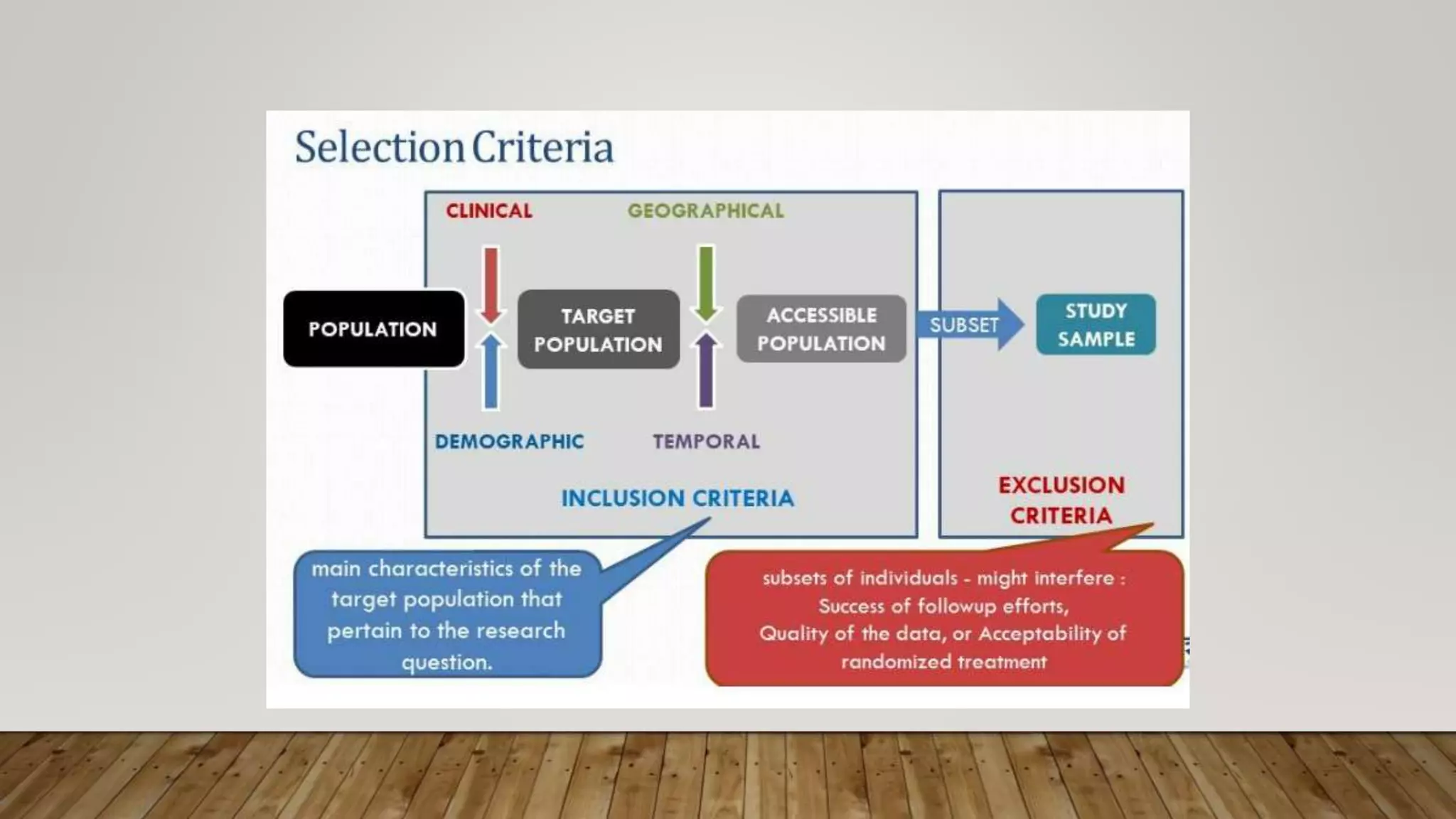
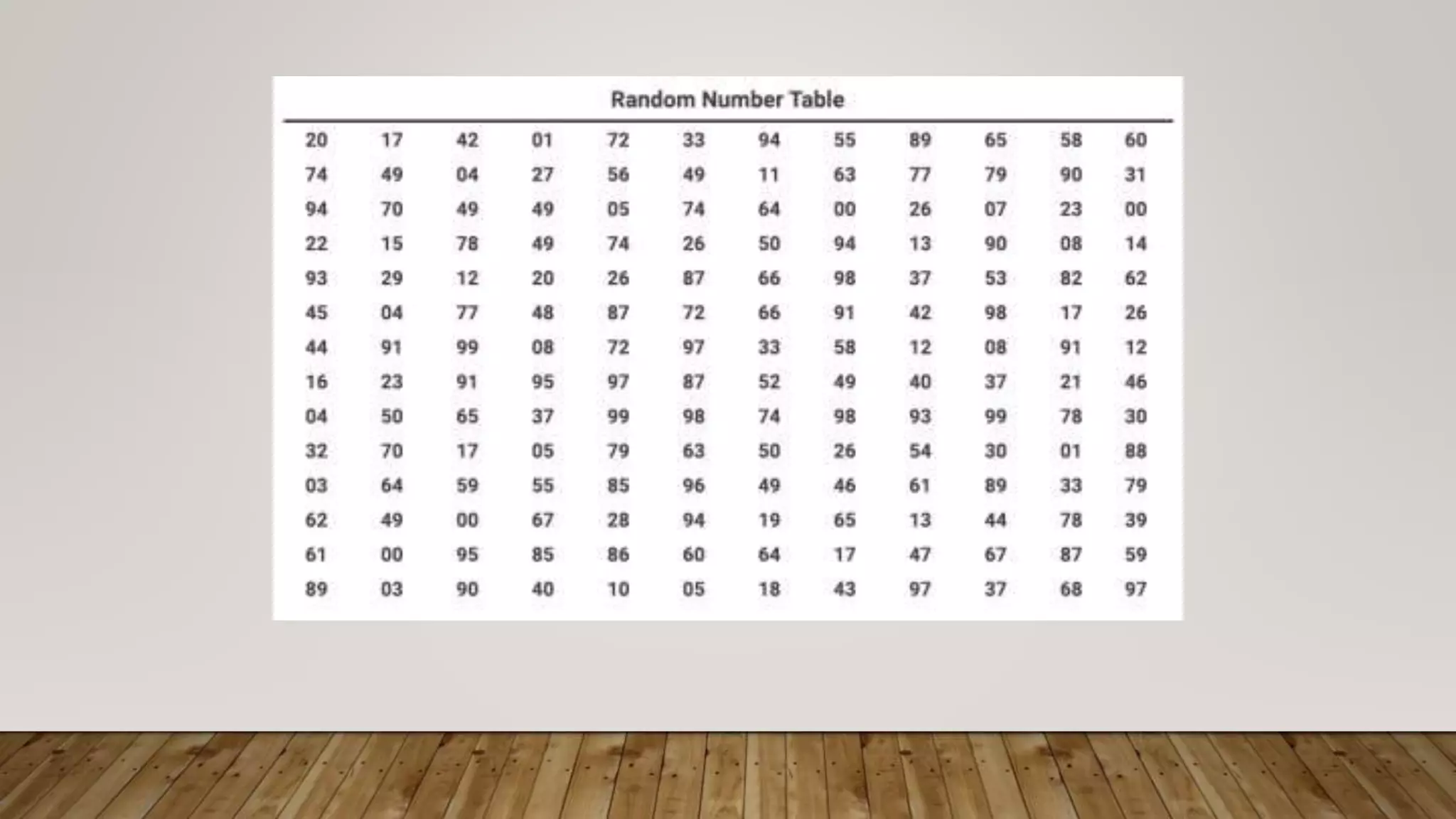
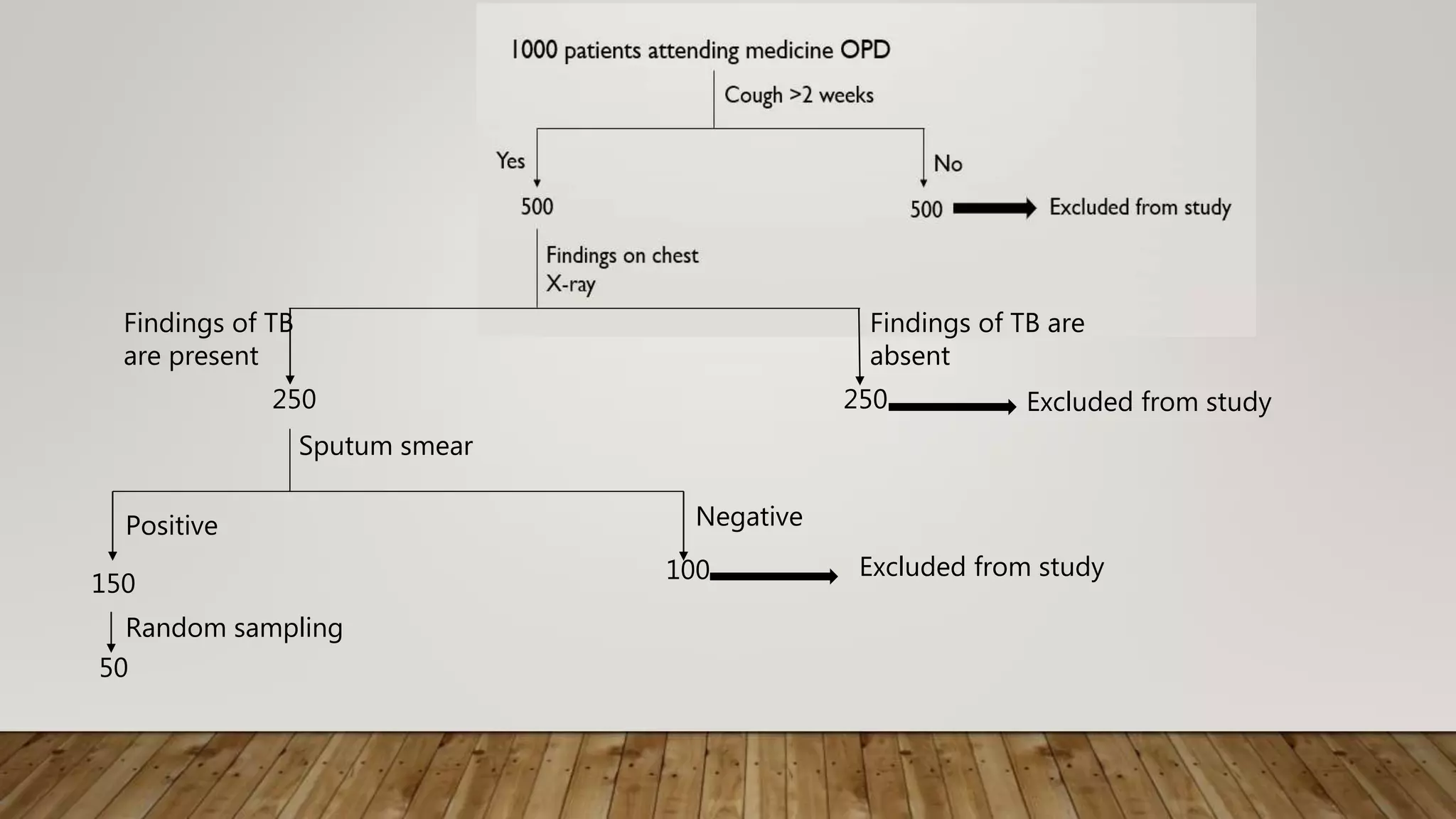
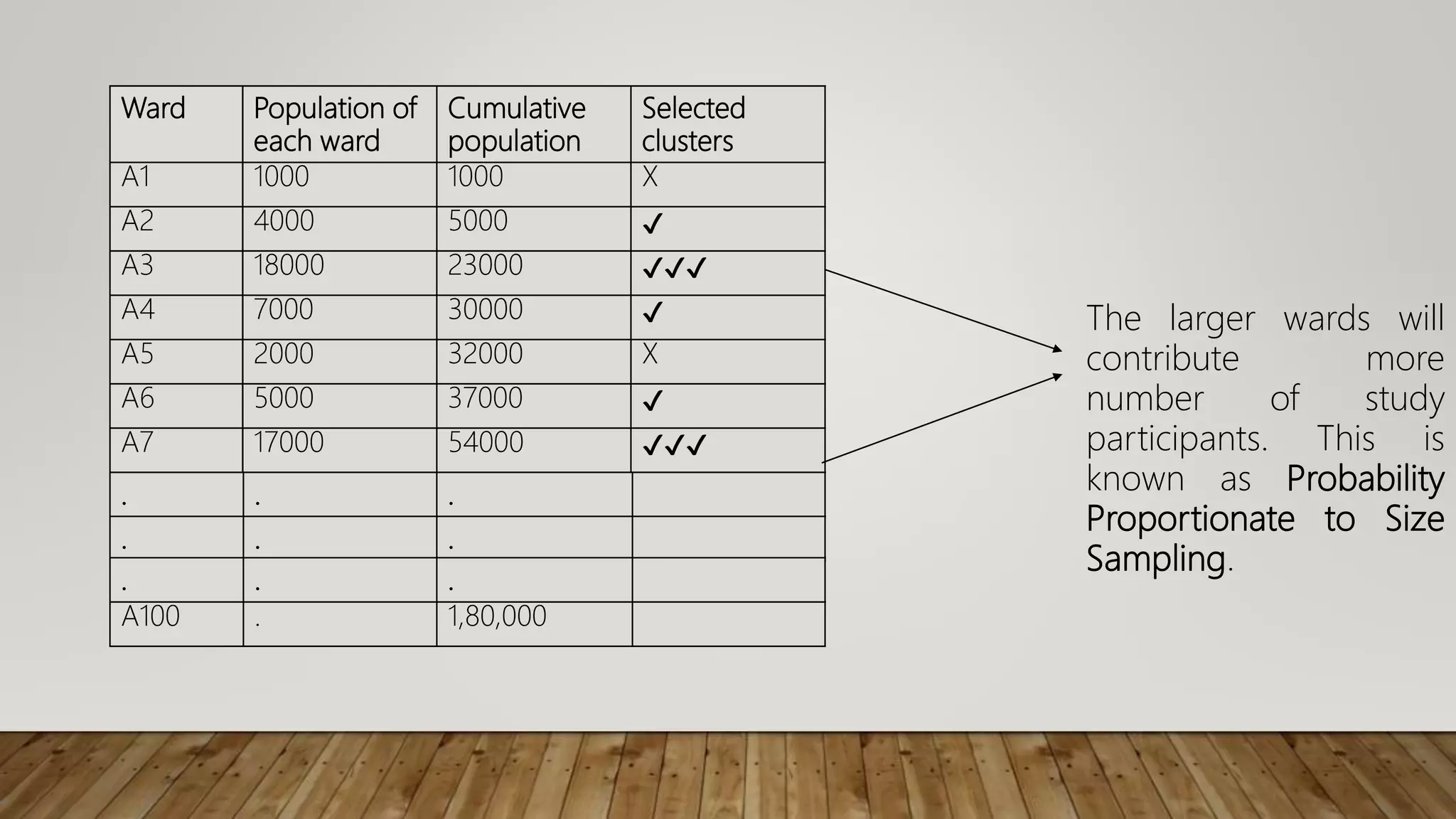
The document discusses the benefits of exercise for both physical and mental health. Regular exercise can improve cardiovascular health, reduce symptoms of depression and anxiety, enhance mood, and reduce stress levels. Staying physically active helps promote overall health and well-being.

1. BASIC COURSE IN
BIOMEDICAL RESEARCH:
SAMPLING
BY- DR UTSAV SHINGHAL
JR-II
PHARMACOLOGY

2. REFERENCES
• Das R, Das PN. Sampling Issues in Research. Biomedical Research
Methodology. New Delhi: Jaypee Brothers Medical Publishers (P)
Ltd; 2011:91-102.
• Sampling. In: Khanal AB, ed. Mahajan’s Methods in Biostatistics For
Medical Students and Research Workers. 8th ed. New Delhi: Jaypee
Brothers Medical Publishers (P) Ltd; 2016:113-27.
• Mehta T. Sampling Methods. Basic Course in Biomedical Research
Handbook. Independently Published; 2021:180-97

3. OUTLINE
• Process of deriving a study sample from the population
• Inclusion and exclusion criteria
• Sampling methods
Random sampling
Simple random sampling
Systematic random sampling
Stratified sampling

4. Multistage random sampling
Multiphase random sampling
Cluster sampling
Non-random sampling
Convenience sampling
Quota sampling
Snowball sampling
Clinical trial sampling

5. Process of deriving a study sample from the
population

6. • Population: A population is the people living in a larger area. For
example, population of India, population of HP
.
• Target population: From the population by applying certain clinical
and demographic characteristics, what we derive is called as the
target population.

7. • For example, if the research question is, I want to study the effect of
low dose metformin to reduce dysmenorrhea among PCOS females
in reproductive age group.
• Here, the clinical characteristics are females sufferings from
polycystic ovarian disease and having a clinical feature of
dysmenorrhea.
• And demographic characteristics are females in the reproductive
age group.

8. • Accessible population: By applying certain geographical and
temporal characteristics, what we get is called as the accessible
population.
• For example, the geographical characteristics are those patients of
target group who are attending the OPD of gynecologist Dr X in
Shimla and temporal characteristics are that only those patients
who visited Dr X’s OPD during the given timeframe of study (from
August 1 to December 31st of year 2022).

9. • Study sample: From accessible population, we obtain a subset
known as Study sample.

10. INCLUSION AND EXCLUSION CRITERIA
• Inclusion criteria: These are the main characteristics (clinical,
demographic, geographic and temporal) of target population that
pertain to research question.
• Exclusion criteria: Characteristics of accessible population which
we do not want to include in our study as
they may interfere with the follow-up efforts (chances of moving out of
Shimla) or with the quality of data (patient is already on metformin therapy)
or
due to the ethical concerns (i.e., non-acceptance to participate in the study)
or
being at a higher risk of possible adverse effects (patients hypersensitive to
metformin or with renal dysfunction).

12. Question: An investigator intends to estimate the prevalence of UTI
among circumscribed children <5 years of age in Shimla. The
researcher selects the study participants from IGMC OPD from
January 1 to December 31st. What will be target population and
accessible population in the given scenario?
Solution:
• Target population: circumscribed children <5 years of age
• Accessible population: circumscribed children <5 years of age attending
IGMC, Shimla OPD from Jan 1 to Dec 31.

13. SAMPLING METHODS
• Sampling: Procedure by which some members of population are
selected as representative of the entire population.
• Sampling unit: Elementary units that will be sampled. For example,
in our study, if we want to estimate that how many needle-sticks do
health care workers experience each year in India. Here the
sampling unit will be health care workers of India.

14. • Sampling frame: List of all sampling units in the population.
• Sampling scheme: Method used to select sampling units from the
sampling frame.

15. TYPES OF SAMPLING
Random sampling/
Non-purposive sampling/
Probability sampling
Non-random sampling/
Purposive sampling/
Non-probability sampling
Simple random sampling Convenience sampling
Systematic random sampling Quota sampling
Stratified random sampling Snowball sampling
Multistage random sampling Clinical trial sampling
Multiphase random sampling
Cluster random sampling

16. RANDOM SAMPLING
• Each unit has an equal chance of being selected in the sample.
• Helps us to draw valid conclusions about the study population.
• Only sampling method which allows the use of statistics.
• Removes bias (for example, Volunteer bias) in the selection of study
subjects.
• Magnitude of error (expressed as Standard error of mean,
proportion and difference) can be measured in probability samples.

17. SIMPLE RANDOM SAMPLING
• Suppose I want to study the average IQ levels in a class of 100
students.
• For this purpose, I want a random sample of 10 students from the
class.
• There are various available methods to do so.
1. Lottery method
• Assign the roll number to all 100 students.
• Note down their roll numbers on 100 cards, put them in a box and
shuffle them well.

18. • Draw one card out of the box and note down the number.
• Put the card back into the box, reshuffle them and draw the second
card.
• Repeat the process until 10 numbers are drawn.
• Reject the cards that are drawn for the second time.
• The 10 cards drawn will thus indicate the roll numbers of 10
students to be included in our study.

19. 2. Random number table booklet:
• In a random number table booklet all the numbers are printed without
an order but each number is equally printed in the book.
• Ask the investigator to close his/her eyes, open the booklet and place
the pointer anywhere.
• Now, move in the predetermined direction (for example, right
direction) to collect 10 numbers.
• If a number is repeated, ignore that number and move to further right
side.

21. 3. Computer software method
4. Currency note method
• Disadvantages of random sampling:
• Does not always achieve the best representation.
• Needs the complete list of all units in the population.

22. Ques: Which of the following about simple random sampling is
false?
A. It needs a complete list of units in the study population.
B. Simple random sampling is a type of purposive sampling.
C. It draws units from the population randomly.
D. It gives equal chance of selection to every unit in the target
population.

23. SYSTEMATIC RANDOM SAMPLING
Procedure:
• First, calculate the sampling interval (k)
k = N/n
Where N = Total population size
And n = Total sample size
• Draw a random number ≤ k for starting by using lottery method.
• Then, draw every kth unit.

24. • For example, I want to study the average IQ levels in a class of 100
students. For this purpose, I want a random sample of 10 students
from the class.
• Here, sampling interval, k = 100/10 = 10
• Now, take 10 cards and serially number them from 1 to 10, put them in
a box and shuffle them.
• One random number is drawn by pulling one card out of the box.
Suppose the number is 6.
• The sample will consist of roll numbers 6, 6+10=16, 16+10=26,….

25. Ques: A researcher wishes to draw a sample from sequentially
numbered houses using a random starting point and then selects
every 6th house, what kind of a sample he/she has
drawn_______________.
Ques: In a neighbourhood with 5000 houses, a researcher wants to
obtain a systematic random sample of 50 houses. What will be the
sampling interval?

26. STRATIFIED RANDOM SAMPLING
• This method is followed when the study population is
heterogenous.
• Here, the heterogenous population is first divided into
homogenous groups or classes called strata.
• The sample is then drawn from each stratum at random in
proportion to its size.
• It is the method of sampling for giving adequate representation to
all strata of society or population such as age, sex, socioeconomic
classes, etc.

27. • For example, if we want to estimate the average Hb levels in a
class of 100 students with 50 boys and 50 classes.
• For this purpose, I want to obtain a sample of 10 students
randomly.
• Here, the sample obtained by simple or stratified random
sampling methods may give us a sample of, say, 7 boys and 3 girls.
• Since the average Hb levels of boys are on higher side as
compared to females, the sample thus obtained may estimate the
average Hb levels on higher side.

28. • So, we need to first divide the entire class into 2 strata of 50 boys
and 50 girls.
• Now, from each strata select 5-5 students by using
simple/systematic random sampling to get a sample of 10 students
with 5 boys and 5 girls.

29. Ques: Based on the number of cigarettes smoked per day, a
researcher divides the population into 3 risk groups for lung cancer
(low-risk, moderate-risk and high-risk). If the researcher then draws
the sample from each of these groups independently, he/she has
created a ____________________ sample.

30. MULTISTAGE RANDOM SAMPLING
• Sampling is done in successive stages and in each stage
randomization should be applied.
• For example, out of over 7 lakh villages in India, I want to include
100 villages in my study.
• The best way will be to go to each of the 37 states and union
territories and select 2-3 villages from each state/UT.
• But it will be very time consuming.

31. • So, better will be to do multistage sampling.
37 States/UT
5 states/UTs
10 districts
2 villages

32. • Advantages of multistage sampling:
• Most feasible approach for large populations
• The complete listing of entire population is not required
• It saves resources
• Disadvantages:
• Leads to generation of several sampling lists.

33. Ques: In a study to measure the prevalence of fluorosis in a district,
towns are sampled first. This is followed by a sample of wards within
the selected towns, and finally a sample of households within the
selected wards. The type of sampling used here is

34. MULTIPHASE RANDOM SAMPLING
• Here, again, the sampling is done in several stages and at each
stage, some part of information is obtained which helps in
inclusion/exclusion of study participants.
• As compared to multistage random sampling, randomization is not
applied at each step in multiphase random sampling.

35. • For example, for my study I want to take a sample of 50 sputum
smear positive cases from 1000 patients attending PGI medicine
OPD.

36. Findings of TB
are present
Findings of TB are
absent
250 250 Excluded from study
Sputum smear
150
100
Negative
Positive
Excluded from study
50
Random sampling

37. CLUSTER SAMPLING
• Used for the evaluation of immunization coverage among children
12-23 months of age in Expanded Programme of Immunization and
Universal Immunization Programme.
• It has an error rate of ± 5%.
• WHO recommended technique for cluster sampling is 30 x 7
technique where 30 are number of clusters and 7 are number of
children in each cluster.
• Total sample size is 210.

38. Procedure:
• Calculate the cumulative population (say, 1,80,000) falling in the
target area.
• Obtain the sampling interval by dividing the total population (1.8
lacs) by number of clusters (30), that will be 6000.
• Now, select a random number less than or equal to sampling
interval having same number of digits (say, 2772).
• This forms the first cluster.

39. • Random number + sampling interval gives the population in 2nd
cluster (2772 + 6000 = 8772).
• 2nd cluster + sampling interval = 3rd cluster (8772 + 6000 = 14772)
and so on.
• This way we will get 30 clusters.
• Or we can simply obtain the list of wards/colonies/villages falling in
the target area and choose 30 out of them by systematic random
sampling as our clusters.

40. Population of
each ward
Cumulative
population
Selected
clusters
1000 1000 X
4000 5000 ✔
18000 23000 ✔✔✔
7000 30000 ✔
2000 32000 X
5000 37000 ✔
17000 54000 ✔✔✔
Ward
A1
A2
A3
A4
A5
A6
A7
The larger wards will
contribute more
number of study
participants. This is
known as Probability
Proportionate to Size
Sampling.
. . .
. . .
. . .
A100 . 1,80,000

41. • Now, all houses within each cluster are numbered.
• The first household in each cluster is chosen randomly, and any
eligible child (i.e., a child between 12-23 months of age) if present is
taken as the part of our sample.
• The surveyor then moves to the ‘next’ household which is defined as
the one whose front door is closest to the one just visited.

42. • This process is continued till all seven eligible subjects are found in
each cluster, irrespective of their immunization status.
• Now, determine the immunization status of these 210 study
participants.

43. • If for some reasons the list of households within a cluster cannot be
prepared,
1. Find out the approximate geographic centre of the cluster.
2. Choose a random direction from the centre
3. Count all households from the centre of the cluster to the edge of
cluster.
4. Randomly select a number between one and the number of
households counted, and this will be the first
household to visit.
1 2 3 55

44. • So, the immunization coverage will be given by
Immunization coverage = x 100
For example, if we want to estimate the BCG vaccine coverage in
Shimla. We did the cluster random sampling and out of 210 study
participants BCG scar was seen in 140 participants. The BCG vaccine
coverage will be 140/210 x 100 = 66.67%
No. of children
immunized
210

45. NON-RANDOM SAMPLING
• Non-probability sampling does not give all the individuals in the
population an equal chance of being selected in the sample.
• There is the possibility of bias in the selection of study participants.
• Non-probability samples are not truly representative of the population.
• Therefore, the inferences drawn from the non-probability samples cannot
be generalized.
• Sampling error cannot be measured.
• Statistical tests cannot be applied.

46. CONVENIENCE SAMPLING
• Sampling done according to convenience of investigator.
• Suppose I have been given a task to determine the average working
hours of PG students of IGMC, Shimla.
• So, ideally what should be done is a sample should be collected
from each department based on the principle of Probability
Proportionate to Size Sampling.

47. • But as per my convenience, I take the sample of, say, 50 PG students
from the non-clinical and para-clinical departments.
• Instead of going to each department, preparing a list of all the PG’s
of all departments and then selecting a sample.

48. QUOTA SAMPLING
• Big sample is divided into smaller quota and within each quota the
sample is selected by non-random method like convenience
sampling.
• Taking the previous example of estimating the average working
hours of PG students of IGMC, Shimla.
• Suppose I call a JR-3 of each department and ask them to make a
list of all JR’s of their respective departments and select a random
sample on my behalf and estimate the average working hours of
JR’s of their department.

49. • Now, the JR-3 goes to his department and as per his convenience
he takes the sample comprising of JR-3 only.
• Instead of taking a stratified random sample of JR-1/2/3.
• So, what we have done here is we have split the whole sample of
JR’S from all departments into smaller quotas of JR’s of each
departments but within each quota of JRs of 1 department, the
sample has been collected by convenience method.

50. SNOWBALL SAMPLING
• Done for hidden populations as for example Commercial Sex
Workers, IV drug addicts, HIV positives, homosexuals.
• Here the researchers first select the people known to them and who
fit into the selection criteria.
• These study subjects are then asked to nominate the people known
to them fulfilling the selection criteria.
• This method continues till a suitable sample size is obtained.

51. 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

52. CLINICAL TRIAL SAMPLING
• Based on first come first serve basis.