This document discusses the history and development of numeral systems. It begins by explaining the key aspects of a numeral system and some of the earliest systems used, such as unary notation. It then describes the development of place-value systems, including the Hindu-Arabic decimal system. Various base systems are covered, such as base-2 (binary), base-5, base-8, base-10, base-12, base-20, and base-60. The document also discusses weighted and non-weighted binary coding systems, including excess-3 code and gray code. The history of binary numbers is outlined, from early concepts developed by ancient Indian and Chinese mathematicians to its modern implementation in digital circuits.

1. T.Satyanarayana Switching Theory and Logic Design
UNIT1: NUMBER SYSTEMS & CODES
• Philosophy of number systems
• Complement representation of negative numbers
• Binary arithmetic
• Binary codes
• Error detecting & error correcting codes
• Hamming codes
HISTORY OF THE NUMERAL SYSTEMS:
A numeral system (or system of numeration) is a linguistic system and mathematical notation for
representing numbers of a given set by symbols in a consistent manner. For example, It allows the numeral
"11" to be interpreted as the binary numeral for three, the decimal numeral for eleven, or other numbers in
different bases.
Ideally, a numeral system will:
• Represent a useful set of numbers (e.g. all whole numbers, integers, or real numbers)
• Give every number represented a unique representation (or at least a standard representation)
• Reflect the algebraic and arithmetic structure of the numbers.
For example, the usual decimal representation of whole numbers gives every whole number a unique
representation as a finite sequence of digits, with the operations of arithmetic (addition, subtraction,
multiplication and division) being present as the standard algorithms of arithmetic. However, when decimal
representation is used for the rational or real numbers, the representation is no longer unique: many rational
numbers have two numerals, a standard one that terminates, such as 2.31, and another that recurs, such as
2.309999999... . Numerals which terminate have no non-zero digits after a given position. For example,
numerals like 2.31 and 2.310 are taken to be the same, except in the experimental sciences, where greater
precision is denoted by the trailing zero.
The most commonly used system of numerals is known as Hindu-Arabic numerals.
Great Indian mathematicians Aryabhatta of Kusumapura (5
th
Century) developed the place value notation.
Brahmagupta (6
th
Century) introduced the symbol zero.
Unary System: Every natural number is represented by a corresponding number of symbols, for example the
number seven would be represented by ///////.
Elias gamma coding which is commonly used in data compression expresses arbitrary-sized numbers by using
unary to indicate the length of a binary numeral. With different symbols for certain new values, if / stands for
one, - for ten and + for 100, then the number 123 as + - - /// without any need for zero. This is called sign-
value notation.
More elegant is a positional system, also known as place-value notation. Again working in base 10, we use ten
different digits 0, ..., 9 and use the position of a digit to signify the power of ten that the digit is to be
multiplied with, as in 304 = 3×100 + 0×10 + 4×1. Note that zero, which is not needed in the other systems, is of
crucial importance here, in order to be able to "skip" a power.
In certain areas of computer science, a modified base-k positional system is used, called bijective numeration,
with digits 1, 2, ..., k (k ≥ 1), and zero being represented by the empty string. This establishes a bijection
between the set of all such digit-strings and the set of non-negative integers, avoiding the non-uniqueness
CMR College of Engineering P a g e | 1

2. T.Satyanarayana Switching Theory and Logic Design
caused by leading zeros. Bijective base-k numeration is also called k-adic notation, not to be confused with p-
adic numbers. Bijective base-1 the same as unary.
Five
A base-5 system (quinary), on the number of fingers, has been used in many cultures for counting. It may
also be regarded as a sub-base of other bases, such as base 10 and base 60.
Eight
A base-8 system (octal), spaces between the fingers , was devised by the Yuki of Northern California, who used
the spaces between the fingers to count, corresponding to the digits one through eight
Ten
The base-10 system (decimal) is the one most commonly used today. It is assumed to have originated because
humans have ten fingers. These systems often use a larger superimposed base.
Twelve
Base-12 systems (duodecimal or dozenal) have been popular. It is the smallest multiple of one, two, three,
four and six. There is still a special word for 12
1
, dozen and a word for 12
2
, gross. Multiples of 12 have been in
common use as English units of resolution in the analog and digital printing world, where 1 point equals 1/72
of an inch and 12 points equal 1 pica, and printer resolutions like 360, 600, 720, 1200 or 1440 dpi (dots per
inch) are common. These are combinations of base-12 and base-10 factors: (3×12)×10, (5×12)×10, (6×12)×10,
(10×12)×10 and (12×12)×10.
Twenty
The Maya civilization and other civilizations of Pre-Columbian Mesoamerica used base-20 (vigesimal).
Remnants of a Gaulish base-20 system also exist in French, as seen today in the names of the numbers from
60 through 99. The Irish language also used base-20 in the past. Danish numerals display a similar base-20
structure.
Sixty
Base 60 (sexagesimal) was used by the Sumerians and their successors in Mesopotamia and survives today in
our system of time (hence the division of an hour into 60 minutes and a minute into 60 seconds) and in our
system of angular measure (a degree is divided into 60 minutes and a minute is divided into 60 seconds). 60
also has a large number of factors, including the first six counting numbers. Base-60 systems are believed to
have originated through the merging of base-10 and base-12 systems.
Dual base (five and twenty)
Many ancient counting systems use 5 as a primary base, almost surely coming from the number of fingers on a
person's hand. Often these systems are supplemented with a secondary base, sometimes ten, sometimes
twenty. In some African languages the word for 5 is the same as "hand" or "fist". Counting continues by adding
1, 2, 3, or 4 to combinations of 5, until the secondary base is reached. In the case of twenty, this word often
means "man complete". This system is referred to as quinquavigesimal. It is found in many languages of the
Sudan region.
CMR College of Engineering P a g e | 2

3. T.Satyanarayana Switching Theory and Logic Design
BINARY
The ancient Indian writer Pingala developed advanced mathematical concepts for describing prosody, and
in doing so presented the first known description of a binary numeral system.
A full set of 8 trigrams and 64 hexagrams, analogous to the 3-bit and 6-bit binary numerals, were known to
the ancient Chinese in the classic text I Ching. An arrangement of the hexagrams of the I Ching, ordered
according to the values of the corresponding binary numbers (from 0 to 63), and a method for generating the
same, was developed by the Chinese scholar and philosopher Shao Yong in the 11th century.
In 1854, British mathematician George Boole published a landmark paper detailing an algebraic system of
logic that would become known as Boolean algebra. His logical calculus was to become instrumental in the
design of digital electronic circuitry.
In 1937, Claude Shannon produced his master's thesis at MIT that implemented Boolean algebra and
binary arithmetic using electronic relays and switches for the first time in history. Entitled A Symbolic
Analysis of Relay and Switching Circuits, Shannon's thesis essentially founded practical digital circuit
design.
In November 1937, George Stibitz, then working at Bell Labs, completed a relay-based computer he dubbed
the "Model K" (for "Kitchen", where he had assembled it), which calculated using binary addition. The
Complex Number Computer was completed by January 8, 1940, was able to calculate complex numbers.
On September 11, 1940, Stibitz was able to send the Complex Number Calculator remote commands over
telephone lines by a teletype.
Binary codes
Binary codes are codes which are represented in binary system with modification from the original ones.
• Weighted Binary codes
• Non Weighted Codes
Weighted binary codes are those which obey the positional weighting principles, each position of the
number represents a specific weight. The binary counting sequence is an example.
Decimal BCD Excess-3 84-2-1 2421 5211 Bi-Quinary 5 0 4 3 2 1 0
8421 5043210
0 0000 0011 0000 0000 0000 0100001 0 X X
1 0001 0100 0111 0001 0001 0100010 1 X X
2 0010 0101 0110 0010 0011 0100100 2 X X
3 0011 0110 0101 0011 0101 0101000 3 X X
4 0100 0111 0100 0100 0111 0110000 4 X X
5 0101 1000 1011 1011 1000 1000001 5 X X
6 0110 1001 1010 1100 1010 1000010 6 X X
7 0111 1010 1001 1101 1100 1000100 7 X X
8 1000 1011 1000 1110 1110 1001000 8 X X
9 1001 1111 1111 1111 1111 1010000 9 X X
CMR College of Engineering P a g e | 3

4. T.Satyanarayana Switching Theory and Logic Design
Reflective Code
A code is said to be reflective when code for 9 is complement for the code for 0, and so is for 8 and
1 codes, 7 and 2, 6 and 3, 5 and 4. Codes 2421, 5211, and excess-3 are reflective, whereas the 8421
code is not.
Sequential Codes
A code is said to be sequential when two subsequent codes, seen as numbers in binary
representation, differ by one. This greatly aids mathematical manipulation of data. The 8421
and Excess-3 codes are sequential, whereas the 2421 and 5211 codes are not.
Non weighted codes
Non weighted codes are codes that are not positionally weighted. That is, each position within
the binary number is not assigned a fixed value. Ex: Excess-3 code
Excess-3 Code
Excess-3 is a non weighted code used to express decimal numbers. The code derives its name
from the fact that each binary code is the corresponding 8421 code plus 0011(3).
Gray Code
The gray code belongs to a class of codes called minimum change codes, in which only one bit in the code
changes when moving from one code to the next. The Gray code is non-weighted code, as the position of bit
does not contain any weight. The gray code is a reflective digital code which has the special property that any
two subsequent numbers codes differ by only one bit. This is also called a unit-distance code. In digital Gray
code has got a special place.
Decimal Binary
Gray Code
Decimal Binary
Gray Code
Number Code Number Code
0 0000 0000 8 1000 1100
1 0001 0001 9 1001 1101
2 0010 0011 10 1010 1111
3 0011 0010 11 1011 1110
4 0100 0110 12 1100 1010
5 0101 0111 13 1101 1011
6 0110 0101 14 1110 1001
7 0111 0100 15 1111 1000
Binary to Gray Conversion
• Gray Code MSB is binary code MSB.
• Gray Code MSB-1 is the XOR of binary code MSB and MSB-1.
• MSB-2 bit of gray code is XOR of MSB-1 and MSB-2 bit of binary code.
• MSB-N bit of gray code is XOR of MSB-N-1 and MSB-N bit of binary code.
CMR College of Engineering P a g e | 4

5. T.Satyanarayana Switching Theory and Logic Design
Error-Detection Codes
Binary information may be transmitted through some communication medium, e.g. using wires or
wireless media. A corrupted bit will have its value changed from 0 to 1 or vice versa. To be able to
detect errors at the receiver end, the sender sends an extra bit (parity bit) with the original binary
message.
A parity bit is an extra bit included with the n-bit binary message to make the total number of 1’s in this
message (including the parity bit) either odd or even. If the parity bit makes the total number of 1’s an odd
(even) number, it is called odd (even) parity. The table shows the required odd (even) parity for a 3-bit
message. At the receiver end, an error is detected if the message does not match have the proper parity
(odd/even). Parity bits can detect the occurrence 1, 3, 5 or any odd number of errors in the transmitted
message. At the receiver end, an error is detected if the message does not match have the proper parity
(odd/even). Parity bits can detect the occurrence 1, 3, 5 or any odd number of errors in the transmitted
message. No error is detectable if the transmitted message has 2 bits in error since the total number of 1’s will
remain even (or odd) as in the original message. In general, a transmitted message with even number of errors
cannot be detected by the parity bit.
Three-Bit Message Odd Even
Parity Parity
Bit Bit
X Y Z P P
0 0 0 1 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 0 1
Binary information may be transmitted through some communication medium, e.g. using wires or
wireless media. Noise in the transmission medium may cause the transmitted binary message to be
corrupted by changing a bit from 0 to 1 or vice versa. To be able to detect errors at the receiver end,
the sender sends an extra bit (parity bit).
Gray Code
The Gray code consists of 16 4-bit code words to represent the decimal Numbers 0 to 15. For Gray
code, successive code words differ by only one bit from one to the next as shown in the table and
further illustrated in the Figure.
CMR College of Engineering P a g e | 5

6. T.Satyanarayana Switching Theory and Logic Design
Error detection codes
The general idea for achieving error detection and correction is to add some redundancy (i.e., some extra
data) to a message, which receivers can use to check consistency of the delivered message, and to recover
data determined to be erroneous. Error-detection and correction schemes can be either systematic or non-
systematic: In a systematic scheme, the transmitter sends the original data, and attaches a fixed number of
check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only error
detection is required, a receiver can simply apply the same algorithm to the received data bits and compare its
output with the received check bits; if the values do not match, an error has occurred at some point during the
transmission. In a system that uses a non-systematic code, the original message is transformed into an
encoded message that has at least as many bits as the original message.
Good error control performance requires the scheme to be selected based on the characteristics of the
communication channel. Common channel models include memory-less models where errors occur randomly
and with a certain probability, and dynamic models where errors occur primarily in bursts. Consequently,
error-detecting and correcting codes can be generally distinguished between random-error-
detecting/correcting and burst-error-detecting/correcting. Some codes can also be suitable for a mixture of
random errors and burst errors.
If the channel capacity cannot be determined, or is highly varying, an error-detection scheme may be
combined with a system for retransmissions of erroneous data. This is known as automatic repeat request
(ARQ), and is most notably used in the Internet. An alternate approach for error control is hybrid automatic
repeat request (HARQ), which is a combination of ARQ and error-correction coding.
Error detection schemes
Error detection is most commonly realized using a suitable hash function (or checksum algorithm). A hash
function adds a fixed-length tag to a message, which enables receivers to verify the delivered message by re-
computing the tag and comparing it with the one provided.
There exists a vast variety of different hash function designs. However, some are of particularly widespread
use because of either their simplicity or their suitability for detecting certain kinds of errors (e.g., the cyclic
redundancy check's performance in detecting burst errors).
Random-error-correcting codes based on minimum distance coding can provide a suitable alternative to hash
functions when a strict guarantee on the minimum number of errors to be detected is desired. Repetition
codes, described below, are special cases of error-correcting codes: although rather inefficient, they find
applications for both error correction and detection due to their simplicity.
Repetition codes
A repetition code is a coding scheme that repeats the bits across a channel to achieve error-free
communication. Given a stream of data to be transmitted, the data is divided into blocks of bits. Each block is
transmitted some predetermined number of times. For example, to send the bit pattern "1011", the four-bit
block can be repeated three times, thus producing "1011 1011 1011". However, if this twelve-bit pattern was
received as "1010 1011 1011" – where the first block is unlike the other two – it can be determined that an
error has occurred.
CMR College of Engineering P a g e | 6

7. T.Satyanarayana Switching Theory and Logic Design
Repetition codes are not very efficient, and can be susceptible to problems if the error occurs in exactly the
same place for each group (e.g., "1010 1010 1010" in the previous example would be detected as correct). The
advantage of repetition codes is that they are extremely simple, and are in fact used in some transmissions of
numbers stations.
Parity bits
A parity bit is a bit that is added to a group of source bits to ensure that the number of set bits (i.e., bits with
value 1) in the outcome is even or odd. It is a very simple scheme that can be used to detect single or any
other odd number (i.e., three, five, etc.) of errors in the output. An even number of flipped bits will make the
parity bit appear correct even though the data is erroneous.
Extensions and variations on the parity bit mechanism are horizontal redundancy checks, vertical redundancy
checks, and "double," "dual," or "diagonal" parity (used in RAID-DP).
Checksums
A checksum of a message is a modular arithmetic sum of message code words of a fixed word length (e.g.,
byte values). The sum may be negated by means of a one's-complement prior to transmission to detect errors
resulting in all-zero messages.
Checksum schemes include parity bits, check digits, and longitudinal redundancy checks. Some checksum
schemes, such as the Luhn algorithm and the Verhoeff algorithm, are specifically designed to detect errors
commonly introduced by humans in writing down or remembering identification numbers.
Cyclic redundancy checks (CRCs)
A cyclic redundancy check (CRC) is a single-burst-error-detecting cyclic code and non-secure hash function
designed to detect accidental changes to digital data in computer networks. It is characterized by specification
of a so-called generator polynomial, which is used as the divisor in a polynomial long division over a finite field,
taking the input data as the dividend, and where the remainder becomes the result.
Cyclic codes have favorable properties in that they are well suited for detecting burst errors. CRCs are
particularly easy to implement in hardware, and are therefore commonly used in digital networks and storage
devices such as hard disk drives.
Even parity is a special case of a cyclic redundancy check, where the single-bit CRC is generated by the divisor
x+1.
Cryptographic hash functions
A cryptographic hash function can provide strong assurances about data integrity, provided that changes of
the data are only accidental (i.e., due to transmission errors). Any modification to the data will likely be
detected through a mismatching hash value. Furthermore, given some hash value, it is infeasible to find some
input data (other than the one given) that will yield the same hash value. Message authentication codes, also
called keyed cryptographic hash functions, provide additional protection against intentional modification by an
attacker.
CMR College of Engineering P a g e | 7

8. T.Satyanarayana Switching Theory and Logic Design
Error-correcting codes
Any error-correcting code can be used for error detection. A code with minimum Hamming distance, d, can
detect up to d-1 errors in a code word. Using minimum-distance-based error-correcting codes for error
detection can be suitable if a strict limit on the minimum number of errors to be detected is desired.
Codes with minimum Hamming distance d=2 are degenerate cases of error-correcting codes, and can be
used to detect single errors. The parity bit is an example of a single-error-detecting code.
The Berger code is an early example of a unidirectional error(-correcting) code that can detect any number of
errors on an asymmetric channel, provided that only transitions of cleared bits to set bits or set bits to cleared
bits can occur.
Hamming Codes
It is an error correction code that separates the bits holding the original value (data bits) from the error
correction bits (check bits), and the difference between the calculated and actual error correction bits is the
position of the bit that's wrong.
Error correction codes are a way to represent a set of symbols so that if any 1 bit of the representation is
accidentally flipped, you can still tell which symbol it was. For example, you can represent two symbols x and y
in 3 bits with the values x=111 and y=000. If you flip any one of the bits of these values, you can still tell which
symbol was intended. If more than 1 bit changes, you can't tell, and you probably get the wrong answer. So it
goes; 1-bit error correction codes can only correct 1-bit changes. If b bits are used to represent the symbols,
then each symbol will own 1+b values: the value representing the symbol, and the values differing from it by 1
bit. In the 3-bit example above, y owned 1+3 values: 000, 001, 010, and 100. Representing n symbols in b bits
will consume n*(1+b) values. If there is a 1-bit error correction code of b bits for n symbols, then n*(1+b) <=
2
b
. An x-bit error correction code requires that n*( (b choose 0) + (b choose 1) + ... + (b choose x) ) <= 2
b
.
The key to the Hamming Code is the use of extra parity bits to allow the identification of a single error. Create
the code word as follows:
1. Mark all bit positions that are powers of two as parity bits. (positions 1, 2, 4, 8, 16, 32, 64, etc.)
2. All other bit positions are for the data to be encoded. (positions 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15,
17, etc.)
3. Each parity bit calculates the parity for some of the bits in the code word. The position of the parity bit
determines the sequence of bits that it alternately checks and skips.
Position 1: check 1 bit, skip 1 bit, check 1 bit, skip 1 bit, etc. (1,3,5,7,9,11,13,15,...) Position
2: check 2 bits, skip 2 bits, check 2 bits, skip 2 bits, etc. (2,3,6,7,10,11,14,15,...)
Position 4: check 4 bits, skip 4 bits, check 4 bits, skip 4 bits, etc. (4,5,6,7,12,13,14,15,20,21,22,23,...)
Position 8: check 8 bits, skip 8 bits, check 8 bits, skip 8 bits, etc. (8-15,24-31,40-47,...)
Position 16: check 16 bits, skip 16 bits, check 16 bits, skip 16 bits, etc. (16-31,48-63,80-95,...)
Position 32: check 32 bits, skip 32 bits, check 32 bits, skip 32 bits, etc. (32-63,96-127,160-
191,...) etc.
4. Set a parity bit to 1 if the total number of ones in the positions it checks is odd. Set a parity bit to 0 if
the total number of ones in the positions it checks is even.
CMR College of Engineering P a g e | 8

9. T.Satyanarayana Switching Theory and Logic Design
Here is an example:
A byte of data: 10011010
Create the data word, leaving spaces for the parity bits: _ _ 1 _ 0 0 1 _ 1 0 1 0
Calculate the parity for each parity bit (a ? represents the bit position being set):
• Position 1 checks bits 1,3,5,7,9,11:
? _ 1 _ 0 0 1 _ 1 0 1 0. Even parity so set position 1 to a 0: 0 _ 1 _ 0 0 1 _ 1 0 1 0
• Position 2 checks bits 2,3,6,7,10,11:
0 ? 1 _ 0 0 1 _ 1 0 1 0. Odd parity so set position 2 to a 1: 0 1 1 _ 0 0 1 _ 1 0 1 0
• Position 4 checks bits 4,5,6,7,12:
0 1 1 ? 0 0 1 _ 1 0 1 0. Odd parity so set position 4 to a 1: 0 1 1 1 0 0 1 _ 1 0 1 0
• Position 8 checks bits 8,9,10,11,12:
0 1 1 1 0 0 1 ? 1 0 1 0. Even parity so set position 8 to a 0: 0 1 1 1 0 0 1 0 1 0 1 0
• Code word: 011100101010.
Finding and fixing a bad bit
The above example created a code word of 011100101010. Suppose the word that was received was
011100101110 instead. Then the receiver could calculate which bit was wrong and correct it. The method is to
verify each check bit. Write down all the incorrect parity bits. Doing so, you will discover that parity bits 2 and
8 are incorrect. It is not an accident that 2 + 8 = 10, and that bit position 10 is the location of the bad bit. In
general, check each parity bit, and add the positions that are wrong, this will give you the location of the bad
bit.
Try one yourself
Test if these code words are correct, assuming they were created using an even parity Hamming Code . If one is
incorrect, indicate what the correct code word should have been. Also, indicate what the original data was.
010101100011
0 1 0 1 0 1 1 0 0 0 1 1 C1 0 Therefore No
0 1 0 1 0 1 1 0 0 0 1 1 C2 0 Error
0 1 0 1 0 1 1 0 0 0 1 1 C3 0
0 1 0 1 0 1 1 0 0 0 1 1 C4 0
111110001100
1 1 1 1 1 0 0 0 1 1 0 0 C1 0 Error is in Bit 4
1 1 1 1 1 0 0 0 1 1 0 0 C2 1
1 1 1 1 1 0 0 0 1 1 0 0 C3 0
1 1 1 1 1 0 0 0 1 1 0 0 C4 0
000010001010
0 0 0 0 1 0 0 0 1 0 1 0 C1 1 Error is in Bit
CMR College of Engineering P a g e | 9

10. T.Satyanarayana Switching Theory and Logic Design
0 0 0 0 1 0 0 0 1 0 1 0 C2 1 7
0 0 0 0 1 0 0 0 1 0 1 0 C3 1
0 0 0 0 1 0 0 0 1 0 1 0 C4 0
Binary Arithmetic:
An ordinary decimal number can be regarded as a polynomial in powers of 10. For example, 423.12
can be regarded as 4 X102 + 2 X101 + 3 X100 + 1 X10
-1
+ 2 X10
-2
. Decimal numbers like this are said to
be expressed in a number system with base, or radix, 10 because there are 10 basic digits (0, 1, 2, …,
9) from which the number system is formulated. In a similar fashion we can express any number N in
a system using any base b. We shall write such a number as (N)b . Whenever (N)b is written, the
convention of always expressing b in base 10 will be followed. Thus (N)b = (pn pn-1 … p1p0 . p-1p-2 … p-
m )b where b is an integer greater than 1 and 0 < pi < b -1. The value of a number represented in this
fashion, which is called positional notation, is given by
(N)b = pn b
n
+ pn-1 b
n-1
+ … + p0 b
0
+p-1b
-1
+p-2b
-2
+…..+p-mb
-m
(N )b
=
∑t
n
= − m pi bi
For decimal numbers, the symbol “.” is called the decimal point; for more general base-b numbers, it
is called the radix point. That portion of the number to the right of the radix point (p-1 p-2 p-m) is
called the fractional part, and the portion to the left of the radix point (pnpn+1 … p0 ) is called the
integral part. Numbers expressed in base 2 are called binary numbers. They are often used in
computers since they require only two coefficient values. The integers from 0 to 15 are given in Table
below for several bases. Since there are no coefficient values for the range 10 to b 1 when b > 10, the
letters A, B, C, . . . are used. Base-8 numbers are called octal numbers, and base-16 numbers are
called hexadecimal numbers. Octal and hexadecimal numbers are often used as a shorthand for
binary numbers. An octal number can be converted into a binary number by converting each of the
octal coefficients individually into its binary equivalent. The same is true for hexadecimal numbers.
This property is true because 8 and 16 are both powers of 2. For numbers with bases that are not a
power of 2, the conversion to binary is more complex.
CMR College of Engineering P a g e | 10

11. T.Satyanarayana Switching Theory and Logic Design
Base
2 3 4 5 .... 8 ..... 10 11 12 16
0001 001 01 01 01 01 01 01 1
0010 002 02 02 02 02 02 02 2
0011 010 03 03 03 03 03 03 3
0100 011 10 04 04 04 04 04 4
0101 012 11 10 05 05 05 05 5
0110 020 12 11 06 06 06 06 6
0111 021 13 12 07 07 07 07 7
(N)b 1000 022 20 13 10 08 08 08 8
1001 100 21 14 11 09 09 09 9
1010 101 22 20 12 10 0A 0A A
1011 102 23 21 13 11 10 0B B
1100 110 30 22 14 12 11 10 C
1101 111 31 23 15 13 12 11 D
1110 112 32 24 16 14 13 12 E
1111 120 33 30 17 15 14 13 F
In converting (N)10 to (N)b the fraction and integer parts are converted separately. First, consider the
integer part (portion to the left of the decimal point). The general conversion procedure is to divide
(N)10 by b, giving (N)10/b and a remainder. The remainder, call it p0 , is the least significant
(rightmost) digit of (N)b. The next least significant digit, p1 , is the remainder of (N)10/b divided by b,
and succeeding digits are obtained by continuing this process. A convenient form for carrying out this
conversion is illustrated in the following example.
(a) (23)10 = (10111)2 (b) (23)10 = (27)8 c) (410)10 = (3120)5
2 23 (Remainder) 8 (Remainder) 5 (Remainder)23 410
5 82 02 11 1 8 2 7
5 16 22 5 1 0 2
2 2 1 5 3 1
0 32 1 0
0 1
Now consider the portion of the number to the right of the decimal point, i.e., the fractional part. The procedure for
converting this is to multiply (N)10 (fractional) by b. If the resulting product is less than 1, then the most significant
(leftmost) digit of the fractional part is 0. If the resulting product is greater than 1, the most significant digit of the
fractional part is the integral part of the product. The next most significant digit is formed by multiplying the
fractional part of this product by b and taking the integral part. The remaining digits are formed by repeating this
CMR College of Engineering P a g e | 11

12. T.Satyanarayana Switching Theory and Logic Design
process. The process may or may not terminate. A convenient form for carrying out this conversion is illustrated
below.
(a)
(0.625)10 = (0.5)8 0.625 x8 = 5.000 0.5
(b) (0.23)10 = (0.001110 . . . )2 0.23 x 2= 0.46 0.0
0.46 x 2= 0.92 0.00
0.92 x 2= 1.84 0.001
0.84 x 2= 1.68 0.0011
0.68 x 2= 1.36 0.00111
0.36 x 2= 0.72 0.001110 …
(c) (27.68)10 = (11011.101011 . . . )2 = (33.53 . . . )8
2 27 0.68 x 2= 1.36 0.1
2 13 1 0.36 x 2= 0.72 0.10
2 6 1 0.72 x 2= 1.44 0.101
2 3 0 0.44 x 2= 0.88 0.1010
2 1 1 0.88 x 2= 1.76 0.10101
0 1 0.76 x 2= 1.52 0.101011 …
8 27 0.68 x 8= 5.44 0.5
8 3 3 0.44 x 8= 3.52 0.53 …
0 3
This example illustrates the simple relationship between the base-2 (binary) system and the base-8 (octal)
system. The binary digits, called bits, are taken three at a time in each direction from the binary point and are
expressed as decimal digits to give the corresponding octal number. For example, 101 in binary is equivalent
to 5 in decimal; so the octal number in part (c) above has a 5 for the most significant digit of the fractional
part. The conversion between octal and binary is so simple that the octal expression is sometimes used as a
convenient shorthand for the corresponding binary number.
When a fraction is converted from one base to another, the conversion may not terminate, since it may not be
possible to represent the fraction exactly in the new base with a finite number of digits. For example, consider
the conversion of (0.1)3 to a base-10 fraction. The result is clearly (0.333 …)10, which can be written as ( 0.3 )10
to indicate that the 3's are repeated indefinitely. It is always possible to represent the result of a conversion of
base in this notation, since the non-terminating fraction must consist of a group of digits which are repeated
indefinitely. For example, (0.2)11 = 2 x 11-1
= (0.1818 …)10 = ( 0.1818 )10 .
CMR College of Engineering P a g e | 12

13. T.Satyanarayana Switching Theory and Logic Design
It should be pointed out that by combining the two conversion methods it is possible to convert between any
two arbitrary bases by using only arithmetic of a third base. For example, to convert (16)7 to base 3, first
convert to base 10,
(16)7 = 1X7
1
+ 6X7
0
= 7 + 6 = (13)10
Then convert (13)10 to base 3,
3 13 (Remainder)
3 4 1 (16)7 = (13)10 = (111)3
3 1 1
3 0 1
Binary Addition
The binary addition table is as follows:
Sum Carry
0 + 0 = 0 0
0 + 1 = 1 0
1 + 0 = 1 0
1 + 1 = 0 1
Addition is performed by writing the numbers to be added in a column with the binary points aligned. The
individual columns of binary digits, or bits, are added in the usual order according to the above addition table.
Note that in adding a column of bits, there is a 1 carry for each pair of 1's in that column. These 1 carries are
treated as bits to be added in the next column to the left. A general rule for addition of a column of numbers
(using any base) is to add the column decimally and divide by the base. The remainder is entered as the sum
for that column, and the quotient is carried to be added in the next column.
Base 2
Carries: 10011 11
1001.011 = (9.375)10
1101.101 =(13.625)10
10111.000 = (23)10 = Sum
Binary Subtraction
The binary subtraction table is as follows:
Difference Borrow
0 - 0 = 0 0
0 - 1 = 1 1
1 - 0 = 1 0
1 - 1 = 0 0
CMR College of Engineering P a g e | 13

14. T.Satyanarayana Switching Theory and Logic Design
Subtraction is performed by writing the minuend over the subtrahend with the binary points aligned and
carrying out the subtraction according to the above table. If a borrow occurs and the next leftmost digit of the
minuend is a 1, it is changed to a 0 and the process of subtraction is then continued from right to left.
Base 2 Base 10
Borrow: 1
0
Minuend 10 2
Subtrahend - 01 -1
-------------------------------
Difference 01 1
-------------------------------
If a borrow occurs and the next leftmost digit of the minuend is a 0, then this 0 is changed to a 1, as is each
successive minuend digit to the left which is equal to 0. The first minuend digit to the left which is equal to 1
is changed to 0, and then the subtraction process is resumed.
Base 2 Base 10
Borrow: 1
0 1 1
Minuend 1 1 0 0 0 24
Subtrahend - 1 0 0 0 1 -17
Difference 0 0 1 1 1 7
Base 2 Base 10
Borrow: 1 1
0 1 0 1 1
Minuend 1 0 1 0 0 0 40
Subtrahend - 0 1 1 0 0 1 -25
Difference 0 0 1 1 1 1 15
Sign-and-magnitude method
One may first approach the problem of representing a number's sign by allocating one sign bit to represent
the sign: set that bit (most significant bit) to 0 for a positive number, and set to 1 for a negative number. The
remaining bits in the number indicate the magnitude (or absolute value). Hence in a byte with only 7 bits
(apart from the sign bit), the magnitude can range from 0000000 (0) to 1111111 (127). Thus you can represent
numbers from −12710 to +12710 once you add the sign bit (the eight bit). A consequence of this representation
is that there are two ways to represent zero, 00000000 (0) and 10000000 (−0). Decimal −43 encoded in an
eight-bit byte this way is 10101011. This approach is directly comparable to the common way of showing a
sign (placing a "+" or "−" next to the number's magnitude). Some early binary computers (e.g. IBM 7090) used
this representation, perhaps because of its natural relation to common usage. Sign-and-magnitude is the most
common way of representing the significand in floating point values.
CMR College of Engineering P a g e | 14

15. T.Satyanarayana Switching Theory and Logic Design
Binary Signed Unsigned
00000000 +0 0
00000001 1 1
... ... ...
01111111 127 127
10000000 −0 128
10000001 −1 129
... ... ...
11111111 −127 255
Ones' complement
Alternatively, a system known as ones' complement can be used to represent negative numbers. The ones'
complement form of a negative binary number is the bitwise NOT applied to it — the "complement" of its
positive counterpart. Like sign-and-magnitude representation, ones' complement has two representations of
0: 00000000 (+0) and 11111111 (−0).
The sum of an n-bit number and its complement is zero. Negative(X)=(2^N – 1) - X The negative of a
1’s complement number is found by inverting each bit, 0 to 1 and 1 to 0. Problem is this scheme has
two values for zero. Finding a negative number is easy and only requires a bit wise complement
operation. However, an addition which produces a “carry” requires an extra add operation for the
carry.
As an example, the ones' complement form of 00101011 (43) becomes 11010100 (−43). The range of signed
numbers using ones' complement is represented by −(2
N−1
−1) to (2
N−1
−1) and +/−0. A conventional eight-bit
byte is −12710 to +12710 with zero being either 00000000 (+0) or 11111111 (−0).
CMR College of Engineering P a g e | 15

16. T.Satyanarayana Switching Theory and Logic Design
Binary
Ones'
Unsigned
To add two numbers represented in this system, one does a
complement conventional binary addition, but it is then necessary to add
value interpretationinterpretation any resulting carry back into the resulting sum. To see why this
is necessary, consider the following example showing the case
00000000 +0 0
of the addition of −1 (11111110) to +2 (00000010).
00000001 1 1
binary decimal... ... ...
11111110 -1
01111101 125 125 + 00000010 +2
01111110 126 126 ............ ...
1 00000000 0 <-- not correct
01111111 127 127
+1 <-- add carry
10000000 −127 128 ........... ...
00000001 1 <-- correct answer10000001 −126 129
10000010 −125 130 Complement/Negate
... ... ...
11111101 −2 253
11111110 −1 254
11111111 −0 255
2’s complement Representation:
The sum of an n-bit number and its 2’s complement is zero. Negative(X) = (2^N) -X = ((2^N – 1)-X)+1.
2’s complement = 1’s complement + 1. Only problem is the range is not symmetric. There is one
more negative number than positive. The negative of a 2’s complement number is found by inverting
each bit, then adding 1. Only problem is the range is not symmetric. There is one more negative
number than positive.
CMR College of Engineering P a g e | 16

17. T.Satyanarayana Switching Theory and Logic Design
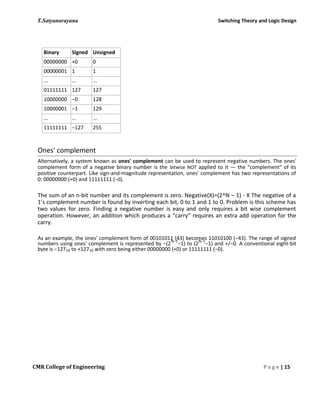
unsigned Sign magnitude 1’s complement 2’s
complement
1111 [15] 0111 [7] 0111 [7] 0111 [7]
1110 0110 0110 0110 [6]
1101 0101 0101 0101 [5]
1100 0100 0100 0100 [4]
1011 0011 0011 0011 [3]
1010 0010 0010 0010 [2]
1001 0001 0001 0001 [1]
1000 0000, 1000[-0] 0000, 1000[-0] 0000 [0]
0111 1001 1110 1111 [-1]
0110 1010 1101 1110 [-2]
0101 1011 1100 1101 [-3]
0100 1100 1011 1100 [-4]
0011 1101 1010 1011 [-5]
0010 1110 1001 1010 [-6]
0001 1111 [-7] 1000 [-7] 1001 [-7]
0000 [0] 1000 [-8]
o Complement/Negate
01011101 number
10100010 invert bits
10100010 + 1 add 1
10100011 2’s Complement
01011101 number
10100011 2’s Complement
1 00000000 (discard carrys in 2’s complement arithmetic)
o Addition
0100 [+4] 0100 [+4]
1101 [-3] 1011 [-5]
1 0001 [+1] [ignore carry] 0 1111 [-1] [no carry]
Signed and Unsigned Arithmetic: (comparisons)
Signed Arithmetic
a) Use: in numerical computation
b) Sign extension required for word size conversion
c) Validity: produces overflow( = signed out-of range) and carry.
CMR College of Engineering P a g e |17

18. T.Satyanarayana Switching Theory and Logic Design
Unsigned Arithmetic
a) Use: in address calculation
b) No negative values
c) No sign extension for word size conversion
d) Validity: only produced carry
( = unsigned overflow = unsigned out-of-range)
Arithmetic Exceptions/Multiword Precision:
Sign Extension:
a) Word size conversion: MSbit of word must be replicated in top of new word.
b) Conversion to smaller word: produces truncation errors, i.e. changed sign
c) Example:
4 bits: 1110 [-2]
8 bits: 1111 1110 [-2] byte
16 bits: 1111 1111 1111 1110 [-2] half word
32 bits: 1111 1111 1111 1111 1111 1111 1111 1110 [-2] word
(register)
Arithmetic Exceptions/Multiword Precision:
Overflow:
a) When a carry occurs from the msb-1 position to the msb and the sign of the is different from
the sign of the two arguments.
b) Overflow can not occur for the addition of two signed numbers with different signs. ( or
subtraction with the same sign)
c) Examples:
0100 [+4] 1100 [-4]
0101 [+5] 1011 [-5]
0 1001 [-7] (9) 1 0111 [+7] (-9)
Carry/Borrow:
a) Occurs during the addition of two unsigned numbers when a carry propagates from the Msbit
of the result.
b) Normally an error for unsigned arithmetic
c) Basis for extended word precision. Words are added/subtracted from LSW to MSW with the
carry from the previous word.
d) Extended word precision for signed number is identical but the MSW addition/subtraction
step uses signed arithmetic.
e) Example:
1100 [12]
1011 [11]
0001 0111 [23] (16 + 7)
CMR College of Engineering P a g e | 18

19. T.Satyanarayana Switching Theory and Logic Design
Questions
1 a What is the Gray code? What are the rules to construct Gray code? Develop the 4 bit Gray
code for the decimal 0 to 15.
b List the XS3 code for decimal 0 to 9
c What are the rules for XS3 addition? Add the two decimal numbers 123 and 658 in XS3
code.
2 Test if these code words are correct, assuming they were created using an even parity
Hamming Code . If one is incorrect, indicate what the correct code word should have been.
Also, indicate what the original data was.
i) 010101100011
ii) 111110001100
iii) 000010001010
3 a Why the binary number system is used in computer design?
b Given the binary numbers a = 1010.1, b = 101.01, c =1001.1 perform the following:
i. a + c
ii.a - b
iii. a. c
c Convert (2AC5.D)16 to binary and then to octal
4 a What is the necessity of binary codes in computers?
b Encode the decimal numbers 0 to 9 by means of the following weighted binary codes.
i. 8 4 2 1
ii. 2 4 2 1
iii. 6 4 2 -3
c Determine which of the above codes are self complementing and why?
5 a Explain the 7 bit Hamming code
b A receiver with even parity Hamming code is received the data as 1110110. Determine the
correct code.
6 The Octal system was devised by the Yuki of Northern California.
Evaluate for A in each case. if (i) (A)2 = (376)8 (ii) (A)10 = (376)8 (iii) (A)5 = (376)8 (iv) (A)12
= (376)8
7 Write brief about i) Weighted Binary codes ii) Non Weighted Codes with at least one
example code examples
8 Write brief about i) Reflective Code ii) Sequential Codes iii) Non weighted codes iv) Excess-
3 Code v) Gray Code vi) Repetition codes vii) Checksums viii) Cyclic redundancy checks
(CRCs) ix) Cryptographic hash functions
9 Write down the procedure for converting a gray code to binary and vice versa (not more
than 4 lines in each case)
10 Write a brief about Hamming Codes (Not more than 5 lines) and hamming distance (about
3 lines)
CMR College of Engineering P a g e |19

20. T.Satyanarayana Switching Theory and Logic Design
11 Check and find if any error in the received message. The message was coded by “Hamming
code” method “0111001”
12 Write the 32 bit pattern that your computer stores number (-2) if it uses i) 1’s complement
method ii) 2’s complement method iii) Signed magnitude method
13 Make a table for 4 bit binary data representation in i) unsigned ii) Sign magnitude iii) 1’s
complement iv) 2’s complement
14 The given data
A = (AC)16 B = (7D)16 C = (F3)16; Find A+B, A+B+C, A-C, A-B
In each case i) if A,B,C are i) Sign magnitude ii) 2’s complement iii) Unsigned magnitude
using binary arithmetic only.
************ ALL THE BEST ************
CMR College of Engineering P a g e | 20