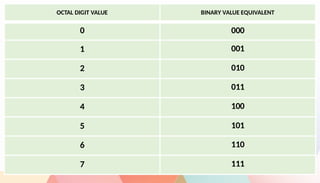
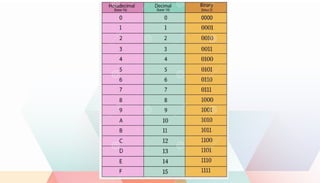
The document explains various computer number systems, including decimal (base-10), binary (base-2), octal (base-8), and hexadecimal (base-16), outlining their characteristics and uses in daily applications and computing. It details how each system represents numbers, with examples of counting and converting between systems. Additionally, it describes methods for converting decimal numbers to binary, octal, and hexadecimal formats.

1. Computer
Number
Systems

2. Decimal Number System
The decimal number system is
the most commonly and widely
used number system. Examples
of its practical and everyday
applications are financial
transactions, measurements,
and general counting.

3. It can also be used in basic
arithmetic calculations,
such as addition,
subtraction, multiplication,
and division. In addition, it
is known as the base-10
number system because it
consists of 10 digits, which
are o to 9.

4. The value of each digit in a decimal number
system has a specific value, depending on its
position within the numerical figure.
For example, in 1452, 1 represents 1000, 4
represents 400, 5 represents 50, and 2
represents 2. The value of this number is the
total of all the digits multiplied by each power.

5. Binary Number System
The binary number system is the basis of all digital
electronic hardware for processing and representing
data. It can also be referred to as machine language
because it is the only language that a machine can
understand. Another name for it is base-2 number
system because there are only two digits, which are
o and 1. Each digit represents a power of 2.

6. Binary systems are not limited to computing;
they are also used in different fields, such as
mathematics, engineering, and digital
technology. Since only o and 1 are used in this
system, counting requires different rules. Begin
with o, with the next number as 1. At this
point, no other number may be used. To
proceed, reset the 1 to o and add 1 to its left,
resulting to 10. Replace the o with 1 to obtain
the next number, 11. Again, only 1's are left.

7. Hence, reset the 1's to o's and add 1 again to its left,
resulting in 100. After obtaining 100, reset the
rightmost o to 1 first, then the middle o to 1, and
continue replacing until only 1s are left before
adding a digit. For instance, counting using the
binary system looks like: 0, 1, 10, 11, 100, 101, 110,
111, 1000, 1001, 1010, and so on. Remember that (a)
if a binary ends in o, count higher by changing this
to 1, and (b) write another digit (1) when all the
numbers are 1 by resetting them to o. The binary
digits in a binary system are called bits.

8. Octal Number System
The octal number system is a computer number
system that uses eight digits, which are o to 7,
used to form other numbers. It is also known as
base-8 number system, since it only uses eight
digits. When counting in the octal number
system, instead of moving to 8 after 7, proceed
to 10, 11, 12, 13, 14, 15, 16, 17, and so on.

9. Similar to the decimal system, each digit in
an octal number has a place value, where
the rightmost digit is the ones place and
the next digit to the left is the eights place.
The octal number system is also a
convenient way to shorten binary numbers
by grouping them into threes. The table
below shows the binary value equivalents
of octal digit values.

10. OCTAL DIGIT VALUE BINARY VALUE EQUIVALENT
0 000
1 001
2 010
3 011
4 100
5 101
6 110
7 111

11. Hexadecimal Number System
The hexadecimal number system is a number system
that uses sixteen (16) symbols composed of number
and letters, which are o to 9 and A to F. that represent
o to 15 in the decimal system. It is also known as
base-16 number system. It can be used to express
large numbers and information using fewer digits.
Similar to the octal number system, to shorten binary
numbers, group them into four pairs. The table below
shows the binary and decimal equivalents of a
hexadecimal digit value.

13. Give the value of each digit of the
Decimal Number System
1. 8910
2. 9510
3. 123510
4. 38410
5. 581410

14. Convert the Octal Digit Value to
Binary Value...
1. 618
2. 4618
3. 5758
4. 58148
5. 12358

15. Convert the Hexadecimal Digit Value
to Binary Value
1. ABC16
2. CEF16
3. 95A16
4. 75F16
5. 8916

16. Conversion of
Computer
Number
Systems

17. Converting between different number systems, such
as binary, octal, decimal, and hexadecimal is
considered a fundamental skill in computer science
and in the field of digital electronics.
Decimal to Other Number System Conversions
Decimal numbers can be converted to binary, octal,
and hexadecimal numbers using division.

18. Decimal to Binary
Follow the steps below to convert decimal numbers to
binary numbers.
1. Write down the decimal number;
2. Repeatedly divide the decimal number by 2, keeping
track of the remainders each time.
3. Write down the remainders in reverse order to get the
binary equivalent.

19. Decimal to Octal
Follow the steps below to convert decimal numbers to
octal numbers.
1. Write down the decimal number;
2. Divide it by 8;
3. Write down the remainder at the rightmost side;
4. Continue dividing the quotient by 8 and writing down
the remainders until the quotient becomes o; then
5. Write down the remainders in reverse order to get the
octal equivalent.

20. Decimal to Hexadecimal
Follow the steps below to convert decimal numbers to
hexadecimal numbers.
1. Write down the decimal number;
2. Divide it by 16;
3. Write down the remainder as the rightmost digit of the
hexadecimal number. If the remainder is equal to 10 to 15,
use hexadecimal letters (A = 10, B = 11, C = 12, D = 13, E
= 14, F = 15);
4. Continue dividing the quotient by 16 and writing down
the remainders until the quotient becomes 0; then
5. Write the remainders in reverse order.