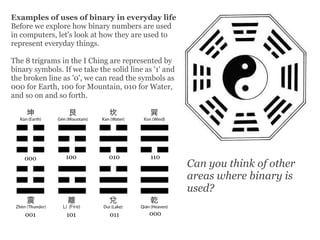
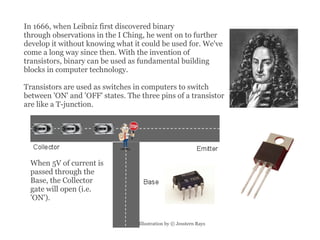
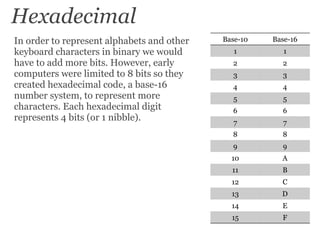
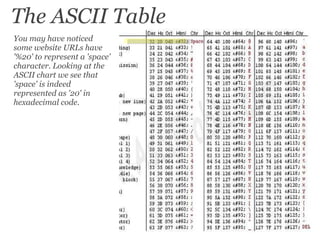
The document discusses various number systems including binary and hexadecimal used in computing. It explains how binary represents numbers as 1s and 0s and is used in electronics like transistors and to represent text, images, and more. Hexadecimal is also introduced which uses 16 symbols to efficiently represent more characters using fewer bits than binary. Color codes in computing are represented using hexadecimal values for red, green, and blue components.

1. Jesstern Rays http://jesstern.com Mathematical concepts and their applications

2. Introduction The aim of this report is to identify the applications of some of the Mathematical concepts discussed in Computing Mathematics. Number systems We explore numerous number systems from different parts of the world and then focus our attention on binary and hexadecimal codes. We explain how binary is used in every day life, how a transistor works and what happens if binary takes over the world. Then we look at an ASCII table and introduce hexadecimals. We also look at how colour codes can be represented in hexadecimal.

3. There are various number systems across the world.

4. There are as many ways to represent numbers as there are languages in the world. The most commonly used number system since the late 15th century is the one we use today derived from the Indian and Arabian number systems. The most important characteristic of the modern numeral system is that there are only 10 symbols to represent all numbers. 1 2 3 4 5 6 7 8 9 0 Computers, despite their complex hardware, operate on a very rudimentary level, that is, in only two states - 'ON' or 'OFF'. The 10 symbol (or base-10) number system we use is far too complicated for computers to process, but can we represent all numbers with just two states? Binary numbers are numbers represented only by two states - '1' or '0'. For computers to be useful we will not only need to represent all real numbers in binary, but also text, images, sound and video. It turns out that binary can indeed do all that. 0 1 1 1 0 0 0 1 0 0 Binary

5. In a digital world, there are only two states. or

6. 0 0 0 0 0 0 0 0 8 bits represents 2 8 = 256 characters

7. Examples of uses of binary in everyday life Before we explore how binary numbers are used in computers, let's look at how they are used to represent everyday things. The 8 trigrams in the I Ching are represented by binary symbols. If we take the solid line as '1' and the broken line as '0', we can read the symbols as 000 for Earth, 100 for Mountain, 010 for Water, and so on and so forth. Can you think of other areas where binary is used? 000 100 010 001 101 011 000 110

8. Here is another example. Binary can be used to pass messages from one party to another from great distances. Before the invention of telecommunications, Morse code was (and is still) used to communicate between vessels using on-off tones, lights, or clicks. Can you decipher this Morse coded message? -- .- - .... ... .-. --- -.-. -.- ...

9. If binary took over the world There's even a blog dedicated to all things binary! http://bitsofbinary.blogspot.com/

10. In 1666, when Leibniz first discovered binary through observations in the I Ching, he went on to further develop it without knowing what it could be used for. We've come a long way since then. With the invention of transistors, binary can be used as fundamental building blocks in computer technology. Transistors are used as switches in computers to switch between 'ON' and 'OFF' states. The three pins of a transistor are like a T-junction. Illustration by © Jesstern Rays When 5V of current is passed through the Base, the Collector gate will open (i.e. 'ON').

11. Hexadecimal In order to represent alphabets and other keyboard characters in binary we would have to add more bits. However, early computers were limited to 8 bits so they created hexadecimal code, a base-16 number system, to represent more characters. Each hexadecimal digit represents 4 bits (or 1 nibble). Base-10 Base-16 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 A 11 B 12 C 13 D 14 E 15 F

12. You may have noticed some website URLs have '%20' to represent a 'space' character. Looking at the ASCII chart we see that 'space' is indeed represented as '20' in hexadecimal code. The ASCII Table

13. C o l o u r codes in hexadecimals

14. The first two digits represents the colour red. Its range being from 0 to 255 in decimal or 00 to FF in hexadecimals. The colour red will be represented as FF0000 in hexadecimal code. Similarly, green is 00FF00 and blue is 0000FF . C o l o u r codes in hexadecimals Colour code: 2468A0 256 3 = 1,777,216 Number of colours that can be represented by this system Red Green Blue Decimals 36 104 160 Hexadecimals 24 68 A0

15. ? Riddle Some real numbers are completely irrational while others are absolutely rational. Integers are naturally rational and natural numbers are positive integers.

16. Here we use sets to represent all real numbers graphically. It gives us a visual interpretation of the their respective definitions and their relation to one another. It’s also an easier way to remember them. Note that natural numbers are the same as positive integers. Real numbers Irrational numbers Rational numbers Integers Natural numbers

17. Source 1. Howard Anton, et al. Applied Finite Mathematics, Fifth Edition, 1992 Chapters 3 and 4, Linear Programming 2. Steven Strogatz Group Think, New York Times Opinionator http://opinionator.blogs.nytimes.com/2010/05/02/group-think/ 3. Cover page image Creative Commons license by stock.xchng http://www.sxc.hu/ 4. On numbers by Internet Looks http://internetlooks.com/onnumbers.html 5. Morse code by Wikipedia http://en.wikipedia.org/wiki/Morse_code 6. How does a transistor work? by Stephen Portz http://www.physlink.com/education/askexperts/ae430.cfm 7. Color code by Wikipedia http://en.wikipedia.org/wiki/Web_colors

18. Jesstern Rays @jessternrays [email_address] http://jesstern.com