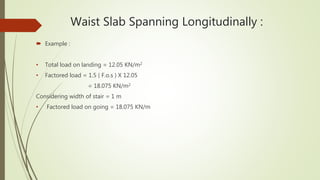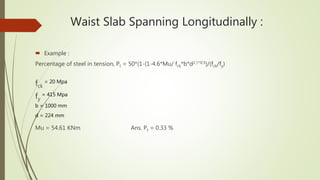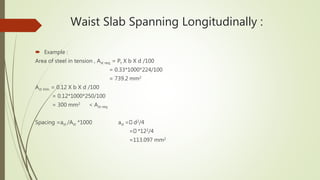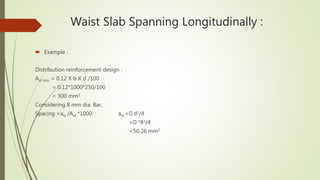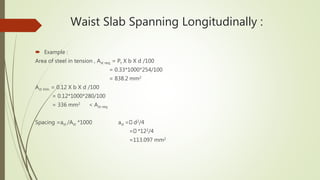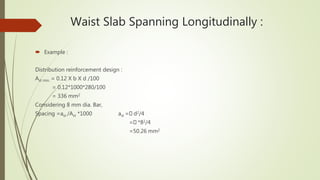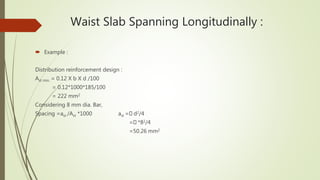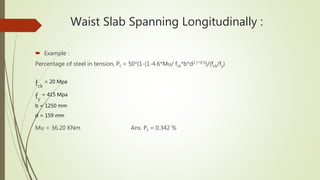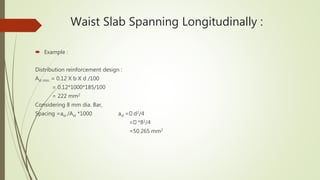This document provides details on the design of staircases, including:
1. It describes the typical components of a staircase like flights, landings, risers, treads, nosings, waist slabs, and soffits.
2. It discusses different types of staircases like straight, quarter turn, dog-legged, open well, spiral and helicoidal.
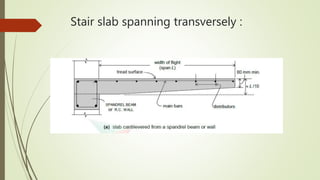
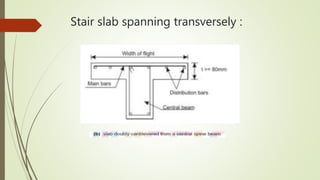
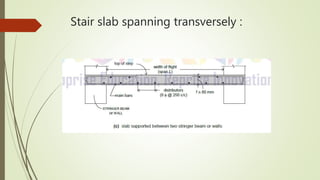
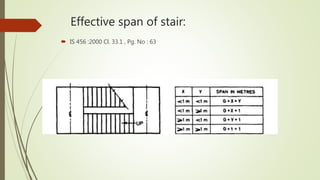
3. It classifies staircases structurally into those with stair slabs spanning transversely or longitudinally and provides examples of each type.
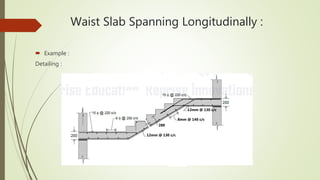
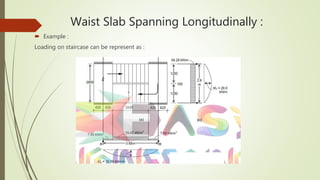
4. It provides an example calculation for the design of a waist slab spanning longitudinally, including loading, bending moment calculation, reinforcement design and checks.






















![Dead Load:
Live loads are generally assumed to act as uniformly distributed loads on the
horizontal projection of the flight, i.e., on the ‘going’. The Loading Code [IS 875 :
1987 (Part II)] recommends,](https://image.slidesharecdn.com/staircasedesign-191228062928/85/Staircase-design-27-320.jpg)