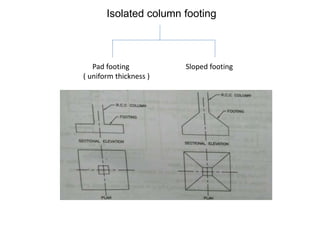
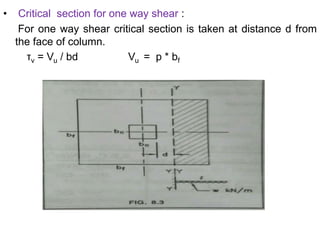
This document discusses the design of an isolated column footing, including: 1) Types of isolated column footings and factors that influence footing size like bearing capacity of soil. 2) Key sections to check for bending moment, shear, and development length. 3) Reinforcement requirements. 4) An example problem where a rectangular isolated sloped footing is designed for a column carrying an axial load of 2000 kN. Design checks are performed for footing size, bending moment, shear, development length, and reinforcement.

1. Isolated Column Footing

2. Content
• Types of isolated column footing
• Bearing capacity of soil
• Critical section
• Check for development length
• Reinforcement requirements
• Example

3. Isolated column footing
Pad footing
( uniform thickness )
Sloped footing

4. Bearing capacity of soil
• The size of footing depends on bearing capacity of soil. The
load on unit area below footing should less than bearing
capacity of soil to prevent settlement of footing.
• Gross bearing capacity :
Total pressure acting at base of footing including self
weight of footing, weight of column , over burden pressure of
soil above footing etc. Is called gross bearing capacity.
The net pressure at base of footing after deducting the
weight of excavated soil is called safe bearing capacity of soil.

5. Safe B.C. = gross B.C. - overburden pressure
qn = q - γ . D
Where , γ = density of soil
D = depth of footing

6. Critical sections
• Critical section for B.M. :
For max. Bending moment critical section is taken on the
face of column. B.M. = w l2 / 2
w = net upward pressure * bf

7. • Critical section for one way shear :
For one way shear critical section is taken at distance d from
the face of column.
τv = Vu / bd Vu = p * bf

8. • Critical section for two way shear :
It is taken at 0.5 d from face of column.
τv = Vu / bo d
Vu = p * hatched area

9. • Check for the development length : ( IS : 456 -2000 , P.42 )
Ld = ɸ * 0.87 fy / 4 τbd
• Reinforcement requirement for footing :
1. Minimum reinforcement ( P.66 )
Fe 250 0.15% of gross area
Fe 415 0.12% of gross area
2. Spacing of bar ( T – 15 , P.46 )
3. Cover : Min. 50 mm cover is required.
Fy N/mm2 Clear distance between bars
250 300 mm
415 180 mm
500 150 mm

10. Example
• Design a rectangular isolated sloped footing for a column of
size 250 mm × 750 mm carrying an axial characteristic load of
2000 kN and reinforced with 10 nos. 25 ɸ bars in M 30 grade
concrete. The allowable bearing on soil is 220 kN/m2 .The
material for footing are grade M 20 concrete and HYSD of
grade fe 415.

11. (a) Size of footing :
characteristic load on column = 2000 kN
Assume self weight of footing = 200 kN
10% of column load
Total load = 2200 kN
Area of footing required = Total load / SBC
= 2200 / 220 = 10 m2
As footing is rectangular size of footing may be selected
such way that effective cantilever projection on both sides
equal.
Difference between dimensions of column = 0.75 – 0.25
= 0.5 m

12. • If b is width of footing,
b ( b + 0.5 ) = 10
b = 2.92 d = 2.95 + 0.5
= 3.45 m
Provide size of footing = 2.95 m × 3.45 m
A = 10.17 m2 > 10 m2 ....... OK
(b) Net upward pressure :
p = Factored column load / Area of footing provided
= 1.5 × 2000 / 10.17
= 294.8 kN/m2

13. (c) Bending moment :
u.d.l along x- direction = p × 2.95
= 294.8 × 2.95
= 869.66 kN.m
u.d.l along y- direction = 294.8 × 2.95
= 1017.06 kN.m
Muy = wl2 / 2 = 869.99 × 1.352 / 2 = 792.48 kN.m
Mux = wl2 / 2 = 1017.06 × 1.352 / 2 = 926.80 kN.m

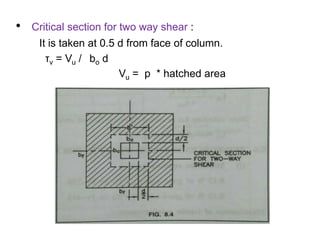
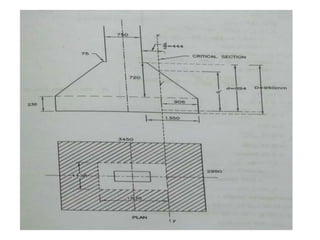
14. (d) Depth of footing :
Mux = 0.138 fck b dx
2
926.80 × 106 = 0.138 × 20 × 900 × dx
2
dx = 610.8 mm
[ b = width of resisting section = 750 + 150
= 900 mm ]
Muy = 0.138 fck b dy
2
792.48 × 106 = 0.138 × 20 × 400 × dy
2
dy = 847.2 mm
[ b = 250 + 150 = 400 mm ]
Try overall depth = 950 mm
Assume 12 ɸ bars for footing

15. • Dy = 950 - 50 – 6 = 894 mm
• Dx = 894 - 12 = 882 mm
Average d = 888 mm
Assume edge depth = 230 mm
(e) Reinforcement :
Along x :
Pt = 0.831 %
Ast = 0.831 / 100 * 400 *894 = 2972 mm2
provide 12 ɸ - 27 nos.
Check for cracking :
Clear distance between bar = (2950 -100-12) /26 = 109.15 mm
c/c distance = 109.15 – 12 =97.15 mm < 180 mm.....O.K.

16. • Along y:
pt = 0.399 %
Ast = 0.399 /100 * 900 * 882 = 3167 mm2
Reinforcement parallel to shorter direction :
β = long side of footing / short side of footing
= 3.45 / 2.95 = 1.169
Width of central band = b = 2950 mm
Ast in central band = 2/(β + 1 ) * total Ast in y direction
= 2920 mm2
Ast required per meter i central band = 2920 / 2.95 = 990 mm2
Provide 12 mm ɸ @ 110 mm c/c in central band.
Remaining steel = 3167 – 2920 = 247 mm2
Width of end band = 3.45 – 2.95 = 0.5 m

18. • 720 / 1350 = y’ / 456 y’ = 243.2 mm
• D’ = y’ + ( 230 – 50 - ɸ/2 )
= 243.2 + ( 230 – 50 – 6)
= 417.2 mm
b’ = width of column + 2d
= 250 + 2*894 = 2038 mm
Vu = S.F. At critical section
= p * hatched area
= 294.8 * 2.95 * 0.456 = 396.56 kN
Mu at critical section = wl2 / 2 = 0.4562 / 2 * 869.66 = 90.42 kn.m
tan β = 720 / 1350 = 0.533

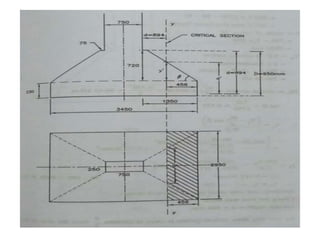
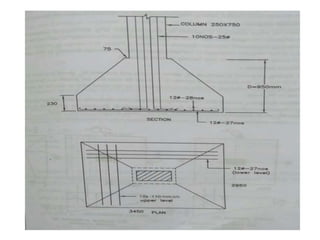
19. • Τv = ( vu - Mu/d
’ tan β ) / b’ d’
= [ 396.56 –(90.42/0.4172) * 0.533 ] *103 / (2038 * 417.2)
= 0.33 N/mm2
Pt = 100 * 3051 / ( 2038* 417.2) = 0.358 %
τc = 0.412 N/mm2
Τv < τc .........O.K.
(g) Check for two way shear :
average depth d = 888 mm
Section id critical at d/2 distance ,
720 / 1350 = y’ / 906 y’ = 483.2 mm
d’ = 483.2 + (230 – 50 – 12 – 6 ) = 645.2 mm
Vu = 294.8 * ( 3.45 * 2.95 - (1.638 * 1.138 )
= 2450.80 kN

21. • τv = Vu / (bo * d’ )
= 2450.80 *103 / ( 5552 * 645.2 )
= 0.684 N/mm2
τc
’ = ks * τc
ks = 0.5 + βc = 0.5 +(250/750 ) = 0.833
τc = 0.25 √ fck = 0.25 √ 20 = 1.11 N/mm2
τc
’ = 0.833 * 1.11 = 0.93 N/mm2
τv < τc
’ ...........OK
Development length :
Ld = 47 ɸ = 47*12 = 564 mm
Ld provided from face = 1350 – 50 = 1300 mm > 564....OK

23. Thank you