２次曲面の極値の問題

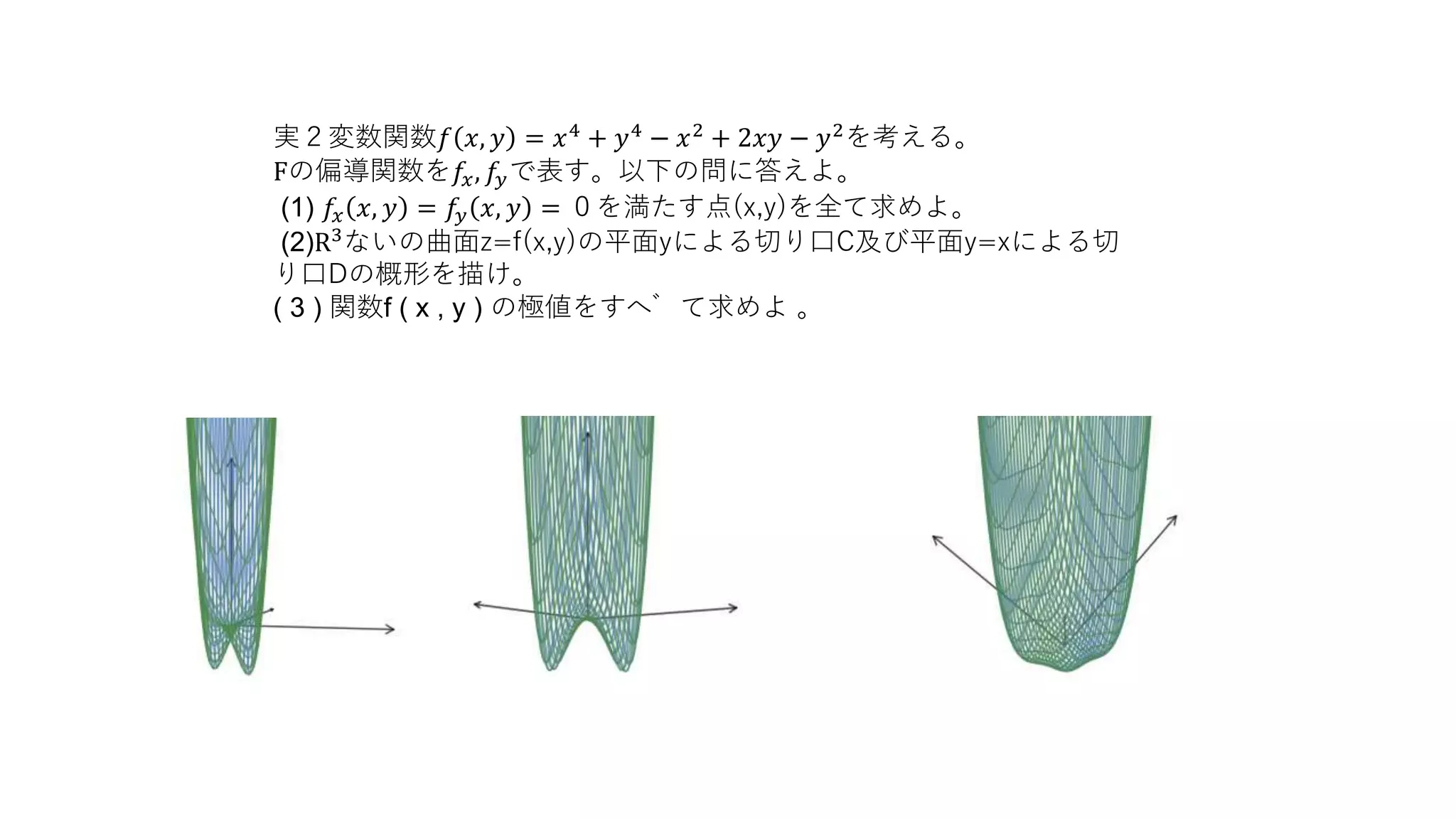
1. 実２変数関数𝑓 𝑥, 𝑦 = 𝑥4
+ 𝑦4
− 𝑥2
+ 2𝑥𝑦 − 𝑦2
を考える。
Fの偏導関数を𝑓𝑥, 𝑓𝑦で表す。以下の問に答えよ。
(1) 𝑓𝑥 𝑥, 𝑦 = 𝑓𝑦 𝑥, 𝑦 = ０を満たす点(x,y)を全て求めよ。
(2)R3
ないの曲面z=f(x,y)の平面yによる切り口C及び平面y=xによる切
り口Dの概形を描け。
( 3 ) 関数f ( x , y ) の極値をすべて求めよ 。

2. 実２変数関数𝑓 𝑥, 𝑦 = 𝑥4
+ 𝑦4
− 𝑥2
+ 2𝑥𝑦 − 𝑦2
を考える。
Fの偏導関数を𝑓𝑥, 𝑓𝑦で表す。以下の問に答えよ。
(1) 𝑓𝑥 𝑥, 𝑦 = 𝑓𝑦 𝑥, 𝑦 = ０を満たす点(x,y)を全て求めよ。
計算
𝑓 𝑥, 𝑦 = 𝑥4
+ 𝑦4
− 𝑥2
+ 2𝑥𝑦 − 𝑦2
より、
𝑓𝑥 = 4𝑥3 − 2𝑥 + 2𝑦 = 0、𝑓𝑦 = 4𝑥3 + 2𝑥 − 2𝑦 = 0→(x,y)=(0,0),(±1, ∓１)
(2)R3
ないの曲面z=f(x,y)の平面yによる切り口C及び平面
y=xによる切り口Dの概形を描け。
C: 𝐹 𝑥 = 𝑓 𝑥, 0 = 𝑥4 − 𝑥2
D:𝐺 𝑥 = 𝑓 𝑥, 𝑥 = 2𝑥4
とする。この時C、Dの概形は次の通りである。
(3)関数f ( x , y ) の極値をすべて求めよ
x,y)=(0,0)の時,(2)の概形よりf(x,y)はこの点の近傍で生の値も負の値も取る。
ある点が極値であるためにはその近傍が全て正の値か、全て負の値でないといけないので
(0,0)は極致を取らない。
次に 𝑓𝑥𝑥 = 12𝑥2 − 2、𝑓𝑥𝑦 = 𝑓𝑦𝑥= 2、𝑓𝑦𝑦 = 12𝑦2 − 2
𝐻 =
𝑓𝑥𝑥 𝑓𝑥𝑦
𝑓𝑦𝑥 𝑓𝑦𝑦
= 24 6𝑥2
𝑦2
− 𝑥2
− 𝑦2
(±1, ∓１)上で𝑓𝑥𝑥 = 10 > 0, ℎ = 96 > 0なので、極小値f(±1, ∓１)=-2である。
(ヘッセ行列と極値の関係は例えば[杉浦]解析学入門2を参照)