積分と漸化式

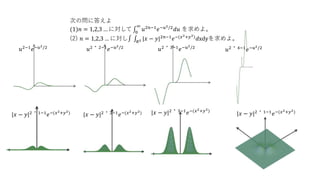
1. 次の問に答えよ
(1)𝑛 = 1,2,3 … に対して 0
∞
𝑢2𝑛−1 𝑒−𝑢2/2 𝑑𝑢 を求めよ。
(2) 𝑛 = 1,2,3 … に対し 𝑅2 |𝑥 − 𝑦|2𝑛−1
𝑒−(𝑥2+𝑦2)
𝑑xdyを求めよ。
𝑢2−1
𝑒−𝑢2/2
𝑢2・2−1
𝑒−𝑢2/2
𝑢2・3−1
𝑒−𝑢2/2
𝑢2・4−1 𝑒−𝑢2/2
|𝑥 − 𝑦|2・1−1
𝑒−(𝑥2+𝑦2)
|𝑥 − 𝑦|2・2−1
𝑒−(𝑥2+𝑦2) |𝑥 − 𝑦|2・3−1 𝑒−(𝑥2+𝑦2)
|𝑥 − 𝑦|2・1−1
𝑒−(𝑥2+𝑦2)

2. 次の問に答えよ
(1)𝑛 = 1,2,3 … に対して 0
∞
𝑢2𝑛−1
𝑒−𝑢2/2
𝑑𝑢 を求めよ。
計算
[0,1)区間で𝑢2𝑛−1 𝑒−𝑢2/2<1より 0
1
𝑢2𝑛−1 𝑒−𝑢2/2 𝑑𝑢 < 1
[1,∞)区間で𝑒 𝑢2/2
= 0
∞ 1
𝑛!
𝑢2
2
𝑘
>
1
n+1 !
u2
2
2
から𝑢2𝑛−1
𝑒−𝑢2/2
＜ 𝑛 + 1 ! 2 𝑛+1
𝑢−3
より
1
∞
𝑢2𝑛−1 𝑒−𝑢2/2 𝑑𝑢 ＜
1
∞
𝑛 + 1 ! 2 𝑛+1 𝑢−3 𝑑𝑢 = 𝑛 + 1 ! 2 𝑛
よって任意のnに対して収束する。
0
∞
𝑢2𝑛−1
𝑒−𝑢2/2
𝑑𝑢 ＝𝐼 𝑛 とおくと
𝐼 𝑛+1 =
0
∞
𝑢2𝑛+1 𝑒−𝑢2/2 𝑑𝑢 ＝ −𝑢2𝑛 𝑒−
𝑢2
2 0
∞
+ 2𝑛𝐼 𝑛 = 2𝑛𝐼 𝑛
(2) 𝑛 = 1,2,3 … に対し 𝑅2 |𝑥 − 𝑦|2𝑛−1
𝑒−(𝑥2+𝑦2)
𝑑xdyを求めよ。
計算
x＝(u+v)/2 y=(-u+v)/2 J(x,y,u,v)=1/2
𝑅2 |𝑥 − 𝑦|2𝑛−1
𝑒−(𝑥2+𝑦2)
𝑑xdy= 𝑅2 𝑢 2𝑛−1
𝑒− 𝑢2+𝑣2 /2 1
2
𝑑ud𝑣=
1
2 −∞
∞
𝑒−
𝑣2
2 𝑑𝑣 −∞
∞
𝑒−
𝑢2
2 𝑑𝑣 𝑢 2𝑛−1
𝑑u
(1)より −∞
∞
𝑒− 𝑢2
𝑑𝑣 𝑢 2𝑛−1
𝑑u=2𝐼 𝑛
ガウス積分より −∞
∞
𝑒−
𝑣2
2 𝑑𝑣= 2π
よって 𝑅2 |𝑥 − 𝑦|2𝑛−1
𝑒−(𝑥2+𝑦2)
𝑑xdy= 2π𝐼 𝑛=2 𝑛−1
𝑛 − 1 ! 2π