Recommended
DOCX
μονώνυμα ταυτότητες - παραγοντοποίηση
DOC
PDF
PPT
PPTX
Α 1.4 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΠΟΛΥΩΝΥΜΩΝ
PDF
PDF
Φύλλο εργασίες στις ρίζες πραγματικών αριθμών - Α΄ Λυκείου
PDF
Διαγώνισμα άλγεβρας Α' λυκείου εξισώσεις - ανισώσεις.pdf
DOC
επαναληπσικες ασκησεις στους μιγαδικοσς αριθμοσς
PPT
PPTX
DOCX
Θέματα μικρών: Αρχιμήδης 2016
PPTX
Α 1.3 ΠΟΛΥΩΝΥΜΑ ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ
PPTX
PPT
Συστήματα γραμμικών εξισώσεων
PDF
Κωνικές τομές - Πλήρες φυλλάδιο (βιβλίο)
PDF
¨Αλγεβρα Εξισώσεις-Ανισώσεις
PDF
Επανάληψη στη Β Γυμνασίου 2017
DOC
PDF
Migadikoi 3o γελ κηφισιασ
PDF
Διαγωνισμα άλγεβρας Α λυκείου ρίζες-με-τις-λύσεις
PDF
Themataeisagwgikwnmathimatikwn
PPTX
PDF
Διαγώνισμα Α΄ Λυκείου (απόλυτα και ρίζες) - Σχ. έτος 2015 - 16
PDF
Διαγώνισμα προσομοίωσης τύπου Δ
PDF
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 2014 2015
DOCX
τυπος 1 επαναληπτικό κριτηριο αξιολογησης θεωριας
PDF
θεωρια μαθηματικων κατευθυνσης Neo 10-3-15
PPTX
Η Πυθαγόρια Φιλοσοφία για Πρωτάρηδες
PPT
More Related Content
DOCX
μονώνυμα ταυτότητες - παραγοντοποίηση
DOC
PDF
PPT
PPTX
Α 1.4 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΠΟΛΥΩΝΥΜΩΝ
PDF
PDF
Φύλλο εργασίες στις ρίζες πραγματικών αριθμών - Α΄ Λυκείου
PDF
Διαγώνισμα άλγεβρας Α' λυκείου εξισώσεις - ανισώσεις.pdf
What's hot
DOC
επαναληπσικες ασκησεις στους μιγαδικοσς αριθμοσς
PPT
PPTX
DOCX
Θέματα μικρών: Αρχιμήδης 2016
PPTX
Α 1.3 ΠΟΛΥΩΝΥΜΑ ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ
PPTX
PPT
Συστήματα γραμμικών εξισώσεων
PDF
Κωνικές τομές - Πλήρες φυλλάδιο (βιβλίο)
PDF
¨Αλγεβρα Εξισώσεις-Ανισώσεις
PDF
Επανάληψη στη Β Γυμνασίου 2017
DOC
PDF
Migadikoi 3o γελ κηφισιασ
PDF
Διαγωνισμα άλγεβρας Α λυκείου ρίζες-με-τις-λύσεις
PDF
Themataeisagwgikwnmathimatikwn
PPTX
PDF
Διαγώνισμα Α΄ Λυκείου (απόλυτα και ρίζες) - Σχ. έτος 2015 - 16
PDF
Διαγώνισμα προσομοίωσης τύπου Δ
PDF
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 2014 2015
DOCX
τυπος 1 επαναληπτικό κριτηριο αξιολογησης θεωριας
PDF
θεωρια μαθηματικων κατευθυνσης Neo 10-3-15
Viewers also liked
PPTX
Η Πυθαγόρια Φιλοσοφία για Πρωτάρηδες
PPT
PPTX
η χρυση τομη στη ζωγραφικη
PPTX
PDF
Μαθηματικά Ε΄ 6.39. ΄΄ Πρόσθεση και αφαίρεση ετερώνυμων κλασμάτων ΄΄
PPT
Πρόσθεση και αφαίρεση ετερώνυμων κλασμάτων
PPT
προβλήματα με πρόσθεση και αφαίρεση κλασμάτων
PPS
προσθεση αφαιρεση κλασματων
Similar to Η ΣΥΝΑΡΤΗΣΗ ψ = αχ
PDF
Επαναληπτικές ασκήσεις ΕΠΑΛ 2017
PDF
ΦΥΛΛΑΔΙΟ ΑΛΥΤΩΝ ΑΣΚΗΣΕΩΝ Γ ΓΕΛ (ΜΑΘΗΜΑΤΙΚΑ) 2020
PDF
25 askiseis algebra_a_lykeiou
DOC
DOC
PDF
Ekpaideutiriadoukaakaiblukeiou2017 170121140246
PDF
Διαγωνίσματα Α και Β Λυκείου Άλγεβρα 2017 και μια άσκηση τριγωνομετρίας με πο...
PDF
Teachers book c class 2018
PDF
λυγάτσικας ζήνων ασκήσεις άλγεβρας B΄λυκείου 2015-6
PDF
Βασικές εκφράσεις Ανάλυσης για μαθητές ΓΕΛ και ΕΠΑΛ
PDF
Σημειώσεις Β΄ Γυμνασίου σε word
PDF
Γραπτή εξέταση στη Γ Λυκείου μέχρι τη σύνθεση [2019]
PDF
PDF
PDF
Revision Algebra A class 2018
PDF
PDF
PDF
ΑΛΓΕΒΡΑ Β΄ Γενικού Λυκείου
PDF
ανάλυση μαθήματα από 1 έως 9 νέο
PDF
Διαγωνίσματα εξοικείωσης περίοδος Ιανουαρίου από τα εκπαιδευτήρια Δούκα
More from ΚΩΣΤΑΣ ΓΚΑΒΕΡΑΣ
PPT
ΣΥΝΑΡΤΗΣΕΙΣ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ2.ppt
PPTX
Το θεώρημα του παπαγάλου-O Aρχιμήδης
PPT
PPTX
PPT
5.3 ΕΝΝΟΙΑ ΤΗΣ ΠΙΘΑΝΟΤΗΤΑΣ
PPTX
PPT
ΔΕΙΓΜΑΤΙΚΟΣ ΧΩΡΟΣ ΕΝΔΕΧΟΜΕΝΑ
PPT
ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ
PPT
νομοι ημιτονων συνημιτονων
PPT
ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ
PPT
PPT
Α 2.5 ΑΝΙΣΟΤΗΤΕΣ - ΑΝΙΣΩΣΕΙΣ
PPT
PPTX
Α 1.5 ΧΑΡΑΚΤΗΡΕΣ ΔΙΑΙΡΕΤΟΤΗΤΑΣ - ΕΚΠ - ΜΚΔ
PPTX
Α 1.4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ - ΔΙΑΙΡΕΤΟΤΗΤΑ
PPTX
A 1.3 ΔΥΝΑΜΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ
PPTX
Α 1.2 ΠΡΟΣΘΕΣΗ - ΑΦΑΙΡΕΣΗ - ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ
PPTX
A 1.3 ΔΥΝΑΜΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ
PPT
PPT
Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
Recently uploaded
PPTX
Επίσκεψη στο ΚΕΠΕΑ Παρανέστι-Ιανουάριος 2026.pptx
PDF
ethniko_apolitirio_parousiasi2026YPAITH.pdf
PDF
3.4 Η συγκρότηση της ρωμαϊκής πολιτείας - Res publica
PDF
ΤΟ ΣΧΟΛΕΙΟ ΜΕΣΑ ΣΤΟΝ ΧΡΟΝΟ ΜΕ ΤΑ 6 ΚΑΠΈΛΑ ΤΗΣ ΣΚΕΨΗΣ
PPTX
ΤΟ ΣΧΟΛΕΙΟ ΣΤΟΝ ΧΡΟΝΟ ΜΕΤΑ ΤΑ ΕΞΙ ΚΑΠΕΛΑ ΤΗΣ ΣΚΕΨΗΣ
PDF
Αμπελόκηποι Αθήνας και Συνεντεύξεις: Συνέντευξη με την κυρία Κατερίνα Μπατσιώτου
PDF
Τροφή για δράση, Εθνική δράση κατά της παχυσαρκίας
PDF
ΕΞΕ - 10503 - 2026 - Ενημέρωση σχετικά με τις απουσίες μαθητών τριών λόγω των...
Η ΣΥΝΑΡΤΗΣΗ ψ = αχ 1. 2. ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1
• Το εμβαδόν Ε τετραγώνου πλευράς α
δίνεται από τον τύπο: ……………
• Να συμπληρώσετε τον πίνακα τιμών που
ακολουθει:
• Ανοίξτε το αρχείο: DRASTHRIOTHTA 1.ggb
Ε = α2
α 0,5 1 1,5 2 2,5 3
Ε
α 0,5 1 1,5 2 2,5 3
Ε 0,25 1 2,25 4 6,25 9
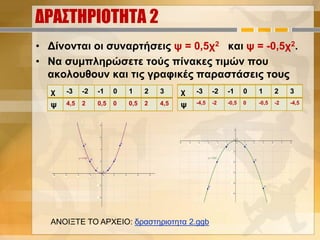
3. ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2
• Δίνονται οι συναρτήσεις ψ = 0,5χ2 και ψ = -0,5χ2.
• Να συμπληρώσετε τούς πίνακες τιμών που
ακολουθουν και τις γραφικές παραστάσεις τους
χ -3 -2 -1 0 1 2 3
ψ
χ -3 -2 -1 0 1 2 3
ψ
χ -3 -2 -1 0 1 2 3
ψ -4,5 -2 -0,5 0 -0,5 -2 -4,5
χ -3 -2 -1 0 1 2 3
ψ 4,5 2 0,5 0 0,5 2 4,5
ΑΝΟΙΞΤΕ ΤΟ ΑΡΧΕΙΟ: δραστηριοτητα 2.ggb
4. ΔΡΑΣΤΗΡΙΟΤΗΤΑ 3
• Ανοίξτε το αρχείο: ΔΡΑΣΤΗΡΙΟΤΗΤΑ 3.ggb
και παρακολουθείστε τις μεταβολές της γραφικής
παράστασης της συνάρτησης ψ = αχ2 για τις
διαφορές τιμές του α.
• Ποια συμπεράσματα που βγάζετε:
5. ΑΣΚΗΣΕΙΣ
• Άσκηση 1
α) H παραβολή y = 6x2 έχει κορυφή το σημείο 0(0, 0).
β) Ο άξονας x΄x είναι άξονας συμμετρίας της
παραβολής y = x2.
γ) ) Οι παραβολές y = 8x2 και y = -8x2 είναι συμμετρικές
ως προς τον άξονα y΄y.
δ) Η συνάρτηση y = 3x2 παίρνει ελάχιστη τιμή την y = 0.
ε) Η συνάρτηση y = -2x2 παίρνει μέγιστη τιμή την y = 0
Να χαρακτηρίσετε τις παρακάτω προτάσεις με (Σ),
αν είναι σωστές ή με (Λ), αν είναι λανθασμένες:
6. 7. Άσκηση 3
• Να βρείτε την εξίσωση της παραβολής του
παρακάτω σχήματος. Να σχεδιάσετε τη
συμμετρική της ως προς τον άξονα x΄x και να
γράψετε την εξίσωσή της.
ΛΥΣΗ
Η συνάρτηση έχει τύπο ψ = αχ2
και αφού το σημείο (-2 ,-1) ανήκει
στη γραφ. Παράσταση της θα την
επαληθεύει, όποτε θα έχουμε:
-1 = α (-2)2 από όπου προκύπτει
α = -1/4 και έτσι έχουμε την
συνάρτηση ψ = -1/4 χ2 ενώ η
συμμετρική της ως προς τον
άξονα χχ΄θα είναι η συνάρτηση:
ψ = 1.4χ2
8.