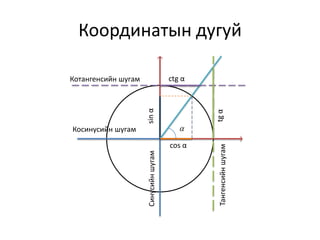
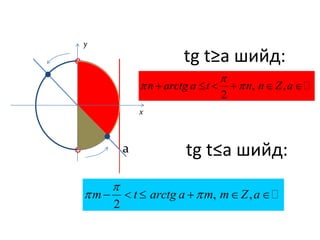
Recommended
PDF
11 soril 31_jishig_daalgavar
PDF
Tootson bodoh matematic lekts
PDF
Soril 32 jishig daalgavar
PDF
Bzd standart olimpiad 2013-iin bodloguud
PDF
Soril 28 jishig daalgavar
PDF
Soril 26 jishig daalgavar
PDF
PDF
11 soril 30_jishig daalgavar
PDF
PDF
Analitek geometrhicheeliin lektsiin huraangui.odon
PDF
Барилгын механик II-ын 3-р бие даалт буюу "Шилжилтийн аргаар статик тодорхой ...
PDF
Барилгын механик III-ын 2-р бие даалт буюу "Статик тодорхой бус рамын тогтвор...
PDF
PDF
Барилгын механик II-ын 2-р бие даалт "Статик тодорхой бус үргэлж дамнуур тооцох"
PDF
ODT
PDF
PDF
Soril 26 jishig daalgavar
PPTX
PDF
Soril 27 jishig daalgavar
PDF
10 soril 27_jishig daalgavar_d
PPT
PDF
10 soril 27_jishig daalgavar_a
PDF
11 soril 25_jishig daalgavar
PDF
Test 23 jishig daalgavar.
PDF
10 soril 27_jishig daalgavar_c
PDF
10 soril 29_jishig daalgavar
PDF
11 soril 28_jishig daalgavar
PPTX
trignometr тригнометр тэгшитгэл
PPT
Classification of Matter Overview. Spring. Day 2
More Related Content
PDF
11 soril 31_jishig_daalgavar
PDF
Tootson bodoh matematic lekts
PDF
Soril 32 jishig daalgavar
PDF
Bzd standart olimpiad 2013-iin bodloguud
PDF
Soril 28 jishig daalgavar
PDF
Soril 26 jishig daalgavar
PDF
PDF
11 soril 30_jishig daalgavar
What's hot
PDF
PDF
Analitek geometrhicheeliin lektsiin huraangui.odon
PDF
Барилгын механик II-ын 3-р бие даалт буюу "Шилжилтийн аргаар статик тодорхой ...
PDF
Барилгын механик III-ын 2-р бие даалт буюу "Статик тодорхой бус рамын тогтвор...
PDF
PDF
Барилгын механик II-ын 2-р бие даалт "Статик тодорхой бус үргэлж дамнуур тооцох"
PDF
ODT
PDF
PDF
Soril 26 jishig daalgavar
PPTX
PDF
Soril 27 jishig daalgavar
PDF
10 soril 27_jishig daalgavar_d
PPT
PDF
10 soril 27_jishig daalgavar_a
PDF
11 soril 25_jishig daalgavar
PDF
Test 23 jishig daalgavar.
PDF
10 soril 27_jishig daalgavar_c
PDF
10 soril 29_jishig daalgavar
PDF
11 soril 28_jishig daalgavar
Viewers also liked
PPTX
trignometr тригнометр тэгшитгэл
PPT
Classification of Matter Overview. Spring. Day 2
PPTX
тригонометр тэгшитгэл бодох аргууд
PDF
Презентация по стратегии АО "Самрук-Қазына"
DOCX
PDF
Cf06 e74e 6242-4cd1-856eb9ffc6c215fe
PDF
47553 c52 14fc-4397-89eca7539c013374
PPT
PDF
DOC
Unit 57 terminology becky doyle
PDF
PDF
Buy or Rent in Columbia SC?
PDF
議会に怒られたので、指名停止について「一応」考えてみた
PPT
PPTX
Explain direxson academy_enq_201312
PPT
PPT
PDF
Kudavi happy valentines day
PDF
Aboriginal Business and International Trade – Canada’s Strategic Advantage (D...
PDF
Indigenous Knowledge Transfer: An Exportable Product Preliminary Research ...
Similar to Координатын дугуй
PDF
PDF
11 soril 31_jishig_daalgavar
PDF
PDF
PDF
800.mn - 2011 Математик ЭЕШ by byambaa avirmed
PDF
9-Математик.pdf 9-р ангид хэрэглэгдэх даалгавар
PDF
PDF
800.mn - 2010 Математик ЭЕШ by byambaa avirmed
PDF
800.mn 2014 mathematics c by byambaa avirmed
PDF
PDF
PDF
800.mn - 2009 Математик ЭЕШ by byambaa avirmed
PDF
ODT
PDF
PDF
4-7-new-хөтөлбөр-ахлах.pdf хөтөлбөр ахлахххх
PDF
ODT
ODT
PDF
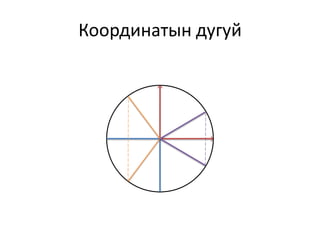
Координатын дугуй 1. 2. Сэдэв сонгосон үндэслэл:
• X-XI ангид математикийн хичээлийг судлах цагийн
24,7%-27,6%-ийг “Тригонометр” сэдэв эзэлж байна.
• Элсэлтийн Ерөнхий Шалгалтын (ЭЕШ) бэлтгэл
болон үндсэн сэдэвт “Тригонометр”-ийн 2-3
бодлого тавигддаг.
• Агуулга ихтэй оюутан суралцагчдад цаашид өргөн
хэрэглэгддэг.
3. Сэдэв сонгосон шалтгаан:
Нийт суралцагчдын хувьд авч үзэхэд
тригонометрийн функцүүдийн үндсэн чанаруудыг
төдийлөн сайн ойлгож мэдээгүйн улмаас зөвхөн
томьёонуудыг цээжилснээр тригонометрийн
тэгшитгэл, тэнцэтгэл бишийг алдаагүй зөв бодож
чадахгүй байна.
4. 5. 6. 7. “ Координатын дугуй” дээр ажиллаж чаддаг байх нь дараах ”5
тоглоомын дасгал”-ыг хэрхэн тоглож байгаагаас шалтгаална.
1. Тоон дугуй, тоон шулууны ялгааг
мэдрэх (тоон шулуун дээр цэг тоо хоёр
харилцан нэгэн утгатай харгалздаг
бол тоон дугуй нь тойргийн нэг цэгт
хэд хэдэн тоо харгалзана.)
“Координатын дугуйн” тойрог дээр
“π” тооны хэсгүүдтэй тэнцүү тоог олж
сурах
8. 2. Координатын дугуй дээр тоон
координаттай цэгүүдийг баримжаалан
олох, координатуудын тэмдгийг тогтоох
3. Координатын дугуйн тойргийн нумыг
илэрхийлэх бичиглэл (аналитик
илэрхийлэл) хийх. Аналитик
илэрхийллээс нь нумыг дүрслэх
9. 4. Координатын дугуйн тойрог дээрх цэгийг харгалзах
өнцгөөр нь, харгалзах өнцгийнх нь тригонометр
функцийн утгаар нь тус тус илэрхийлэх. (Туйлын
координатын системээс декартын координатын
системд шилжих)
5. Өгсөн нөхцлийг хангах цэгийг /нумын цэгүүдийг/
координатын дугуйн тойрог дээр байгуулах
10. Эдгээр “5 тоглоомын дасгал”-
ыг дараах “7 дадлага ажил”-
уудаар “гаргалгаа” хийлгэх
явцад “чадвар” болно.
11. Дадлага №1 Координатын дугуй дээр
тригонометрийн үндсэн функцүүдийг “тодорхойлох”
)sin;(cos);( MyxM
x
y
);( yxM
α
x
y1
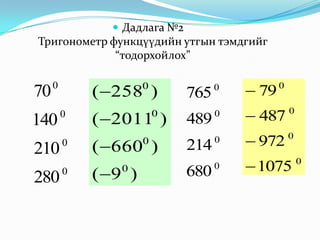
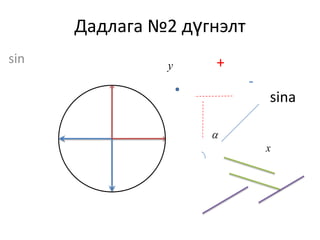
12. Дадлага №2
Тригонометр функцүүдийн утгын тэмдгийг
“тодорхойлох”
0
0
0
0
280
210
140
70
)9(
)660(
)2011(
)258(
0
0
0
0
0
0
0
0
680
214
489
765
0
0
0
0
1075
972
487
79
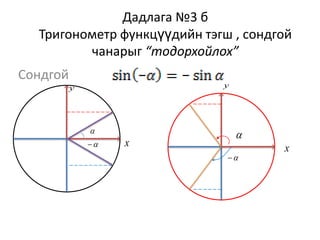
13. 14. 15. 16. 17. 18. Дадлага №3 в
Тригонометр функцүүдийн үелэх чанарыг
“тодорхойлох”
2
0
0
0
0
1075
972
487
79
I мөч: )355()360(21075 000
II мөч: 000
252)360(2972
III мөч: )37()360(1487 000
IY мөч: 0000
11270)79(279
23600
0
180
19. 20. 21. 22. 23. 28. ,( , , )tgx a
Дадлага №7
тэнцэтгэл биш бодох
29. 30. 31. 32. Нумд тохирох тэнцэтгэл бишийг бич
11
6 6
t
3
cos
2
t
300
?
y
x0
6
6
11
6
11
62?
2
3
6cos
33. Тэнцэтгэл бишийг бод
5
2 2
6 2 6
5
4 4 ,
3 3
x
l l
l x l l Z
1
sin 0
2 2
x
-300
y
x
6
5
6
0
2
1
2sin x
626
5
x2
1
34. 35. 36. Зорилго: “Нэгж тойрог” ашиглаж тригонометр
тэнцэтгэл биш бодохМэдлэг: Тангенсийн тэнцэтгэл
бишийн хэлбэрүүд, тангенсийн
шугам,тэнцэтгэл бишийн шийд
Чадвар: Хялбар тэнцэтгэл бишийг
тухайн тохиолдлоос ерөнхий
тохиолдолд бодож сурах, шийд зөв
бичих, шийдийг дүрслэх
Хэрэглээ: Асуудлыг хялбар аргаар
шийдэж сурах
37. • 1. a=-2 үед tg t ≤-2 2. tg t ≥ -2
tg t≥a (≤, >,< )
y
x
(1;-2)
arctg(-2)=- arctg2
2
2
1. 2 ,
2
n t arctg n n
2. 2 ,
2
arctg n t n n
0
38. Тэнцэтгэл бишийг бодож
шийдийг нэгж тойрог дээр
дүрсэл.
. 1; 1
. 1; 1
. 1; 1
. 3; 3
. 3; 3
Atgx tgx
B tgx tgx
C tgx tgx
D tgx tgx
E tgx tgx
39. Хариу:
1. ,
4 2
2. ,
2 4
A k x k k
A k x k k
1. ,
4 2
2. ,
2 4
B k x k k
B k x k k
1. ,
4 2
2. ,
2 4
C k x k k
C k x k k
1. ,
2 3
2. ,
3 2
D k x k k
D k x k k
1. ,
3 2
2. ,
2 3
E k x k k
E k x k k
40. tg x ≤a (tg x ≥a) тригонометр
тэнцэтгэл биш бодох загвар
Координатын эх дээр төвтэй нэгж тойрог зурж
тангенсийн тасралтын цэг ( ) ийг
тойрог дээр тэмдэглэнэ.
Тангенсийн шугам ( ) дээр (1;а) цэгийг
тэмдэглэж , (1;а) цэг болон координатын эхийг
дайрсан шулуун татаж тойрогтой огтлолцох
цэгүүдийг тэмдэглэж утгыг бичнэ.
Шийдийг дүрсэлж хариуг бичнэ
◦ Жишээ 1: tg x ≤
◦ Жишээ 2: tg x >-2
,
2
x k k Z
1x
3
41. y
x
a
tg t≥a шийд:
tg t≤a шийд:
, ,
2
n arctg a t n n Z a
, ,
2
m t arctg a m m Z a
42. Дүгнэлт :Шийдийг тохируул.
1. tgx=1
2. tgx>1
3. ctgx=-1
4. tgx ≤-1
5. sinx=0
. ,
. ,
4
. ,
2 4
. ,
4 2
3
. ,
4
a x n n
b x m m
c l x l l
d n x n n
e x k k
Хариу: 1.b 2.d 3.e 4.c 5.a
43. y
x
a
tg t≥a шийд:
tg t≤a шийд:
, ,
2
n arctg a t n n Z a
, ,
2
m t arctg a m m Z a
44. Даалгавар
Сурах бичгийн 54-р хуудас. № 101-103
Сурах бичгийн 54-р хуудас. № 104-108
МУИС-ийн тест 130-р хуудас №508-510
ХИЧЭЭЛД АМЖИЛТТАЙ ОРОЛЦСОН та бүхэнд
БАЯРЛАЛАА.
45. • 1. a=-0.5 үед ctg t ≤-0.5 2. ctg t ≥ -0.5
ctg t≥a (≤, >,< )
y
x
(-0.5;1)
1
2arcctg
1
1. ,
2
arcctg n t n n
1
2. ,
2
n t arcctg n n
0 20
46. Тэнцэтгэл бишийг бодож
шийдийг нэгж тойрог дээр
дүрсэл.
. 1; 1
. 1; 1
. 1; 1
. 3; 3
. 3; 3
E ctgx ctgx
D ctgx ctgx
C ctgx ctgx
B ctgx ctgx
Actgx ctgx
47. Хариу:5
1. ,
6
5
2. ,
6
A k x k k
A k x k k
1. ,
6
2. ,
6
B k x k k
B k x k k
1. ,
4
2. ,
4
C k x k k
C k x k k
3
1. ,
4
3
2. ,
4
D k x k k
D k x k k
1. ,
4
2. ,
4
E k x k k
E k x k k
48. ctg x ≤a (ctg x ≥a) тригонометр
тэнцэтгэл биш бодох загвар Координатын эх дээр төвтэй нэгж тойрог зурна.
Котангенсийн тасралтын цэг ( ) ийг
тойрог дээр тэмдэглэнэ
Котангенсийн шугам ( ) дээр (а;1) цэгийг
тэмдэглэж, (а;1) цэг болон координатын эхийг
дайрсан шулуун татаж тойрогтой огтлолцох
цэгүүдийг тэмдэглэж, утгыг олж бичнэ.
Шийдийг дүрсэлж хариуг бичнэ
Жишээ 1: ctg x ≥ -
Жишээ 2: ctg x <
,x k k Z
1y
3
3
3
49. 50. Дүгнэлт :Шийдийг тохируул.
1. tgx=1
2. ctgx>1
3. ctgx=-1
4. tgx ≤-1
5. sinx=0
. ,
. ,
4
. ,
2 4
. ,
4
3
. ,
4
a x n n
b x m m
c l x l l
d n x n n
e x k k
Хариу: 1.b 2.d 3.e 4.c 5.a
51. 0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
1 2 3 4 5
3.96
3.89
3.61 3.68
4.14
3.81
4.06
3.89 3.83 3.92
3.41
3.86
3.49 3.59 3.62
Бодлогын дугаар
Дадлагуудын дундаж үзүүлэлт
10-3 анги
10-6 анги
10-8 анги