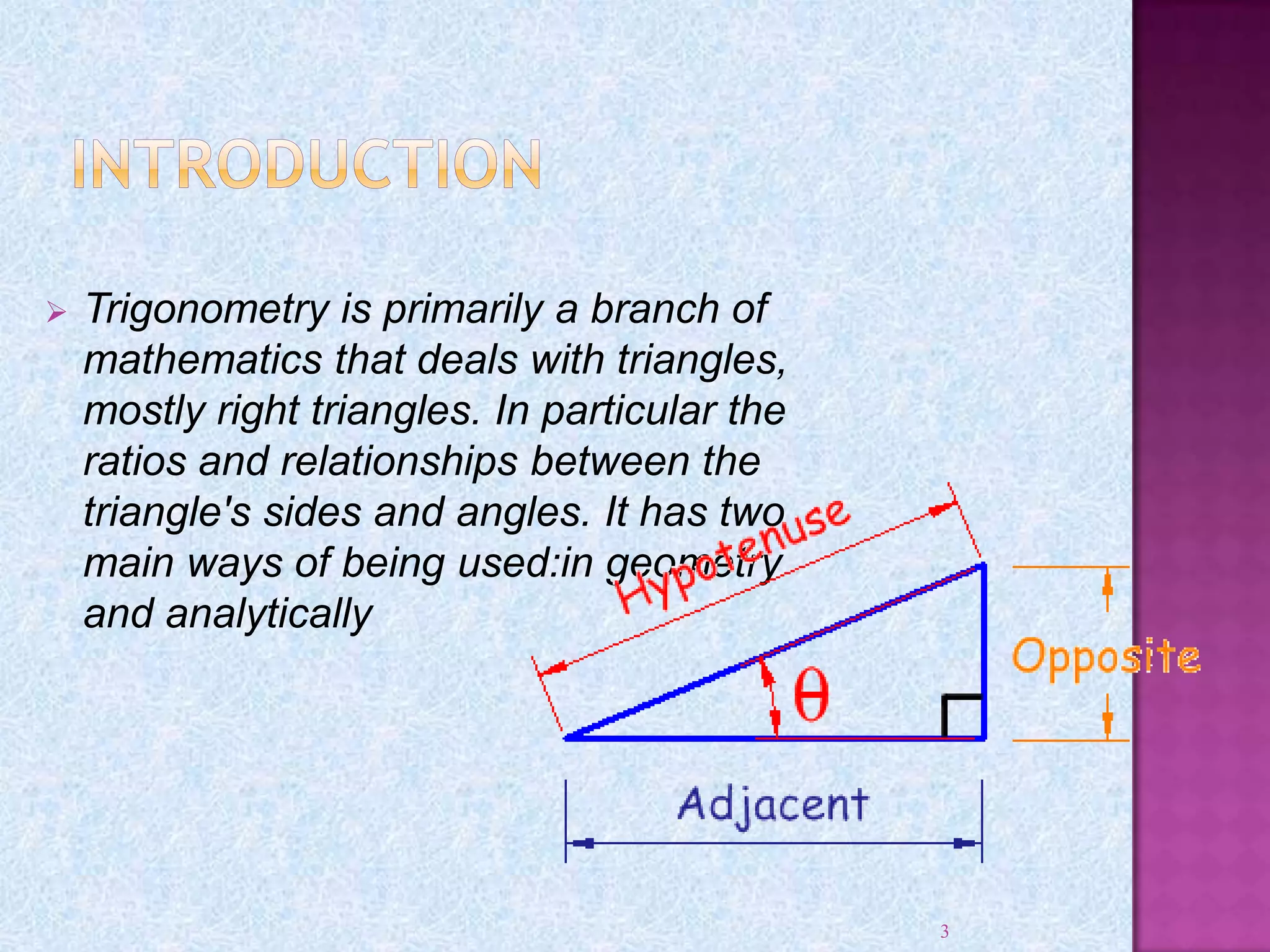
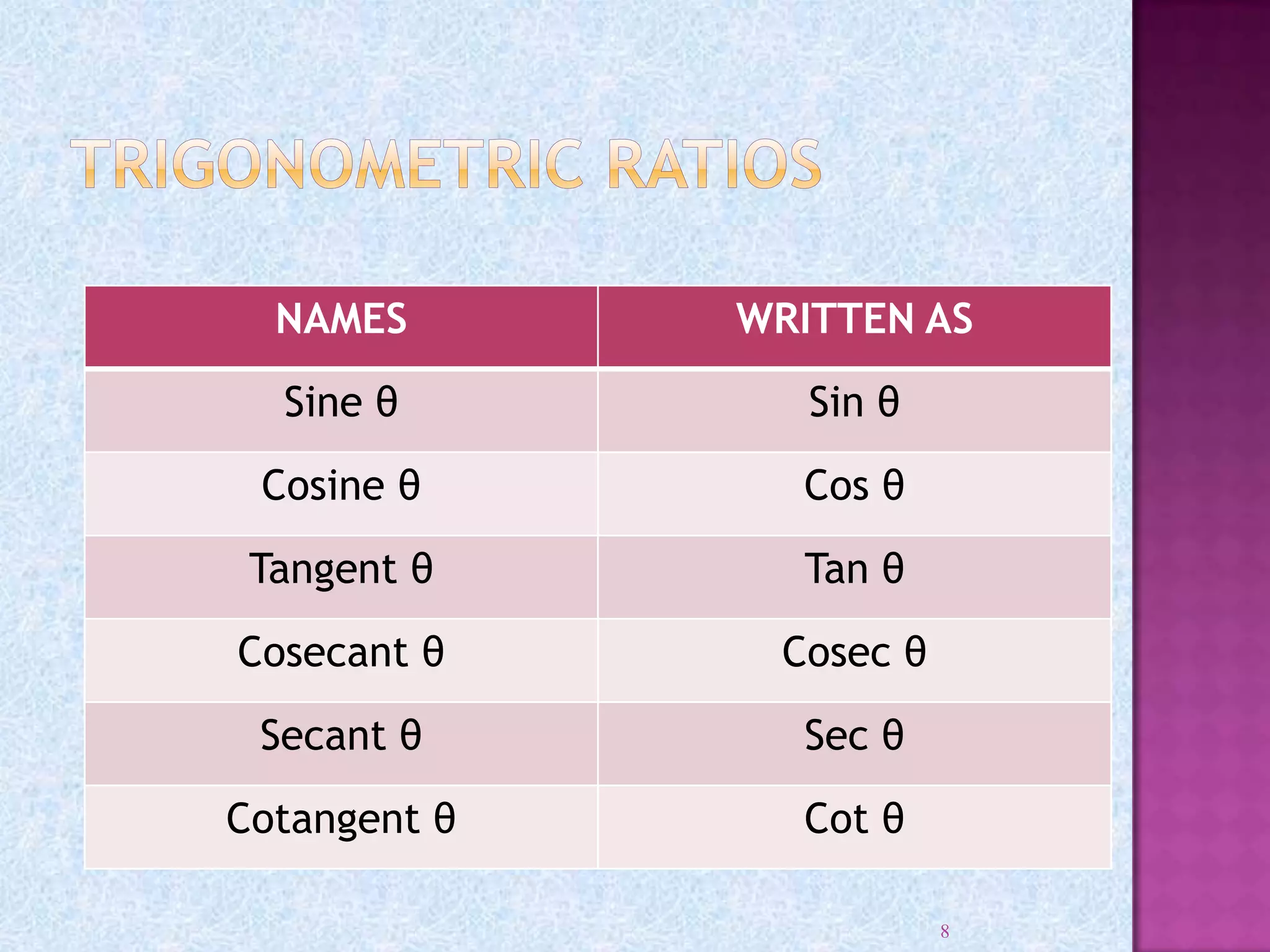
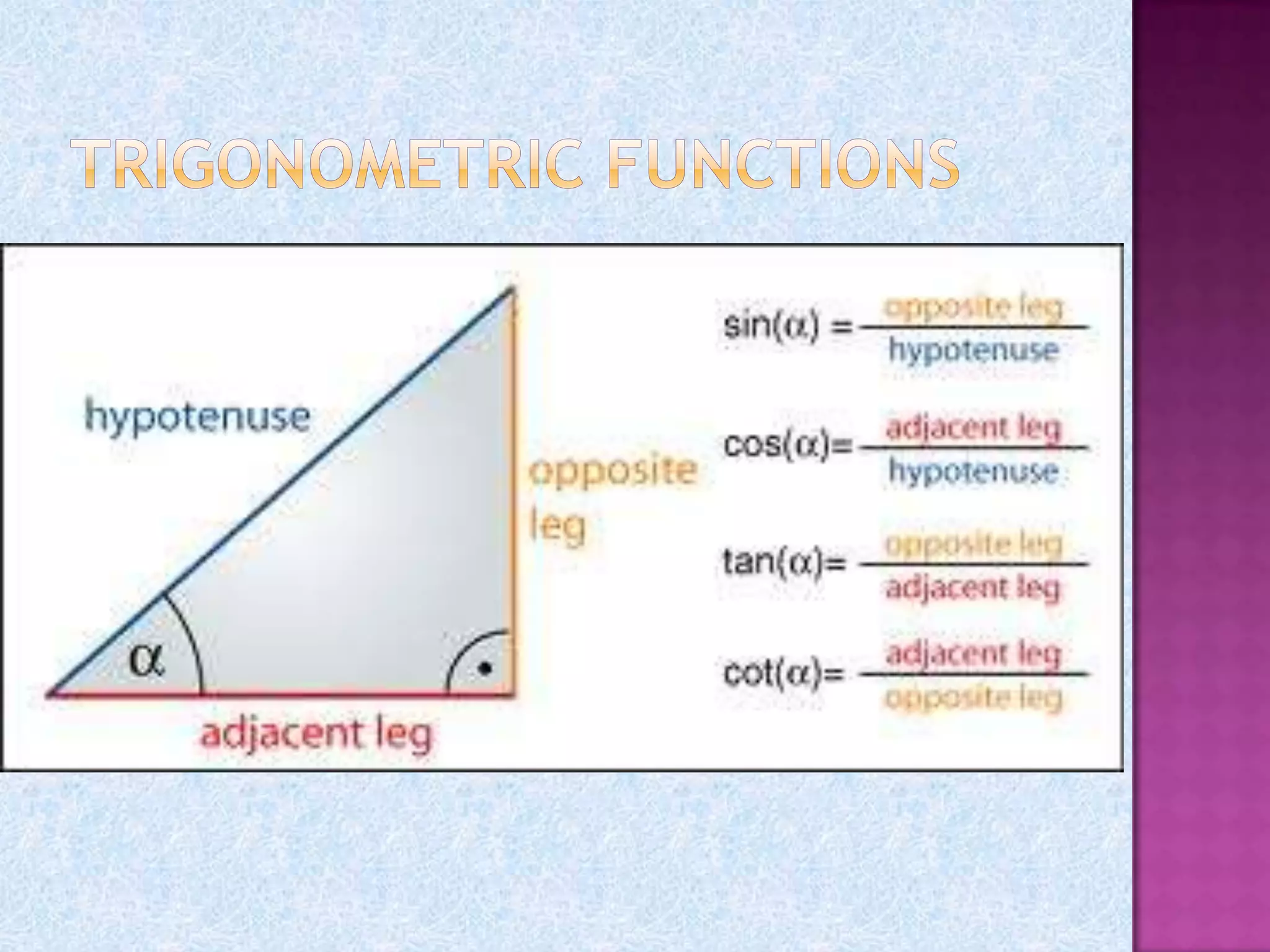
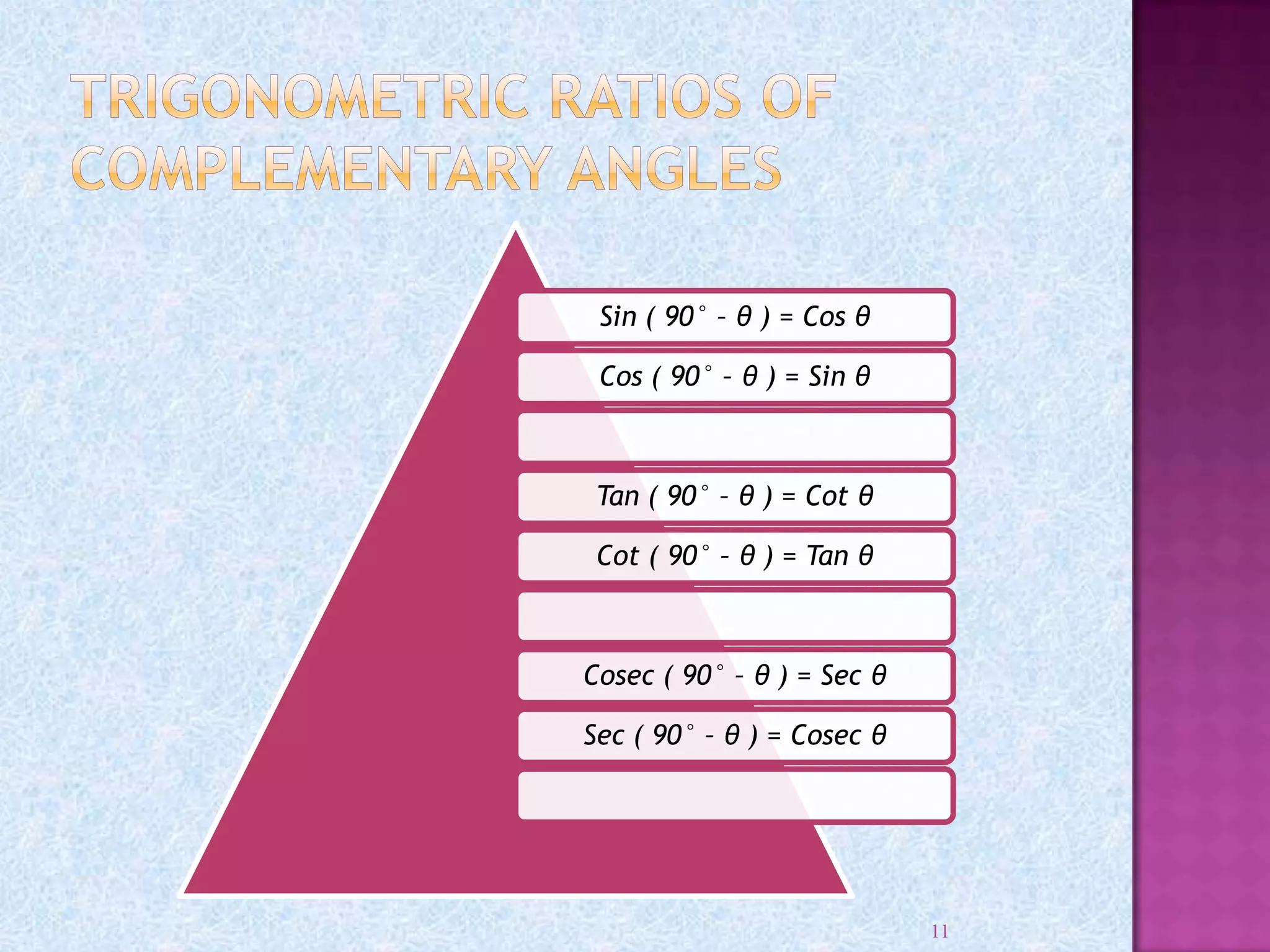
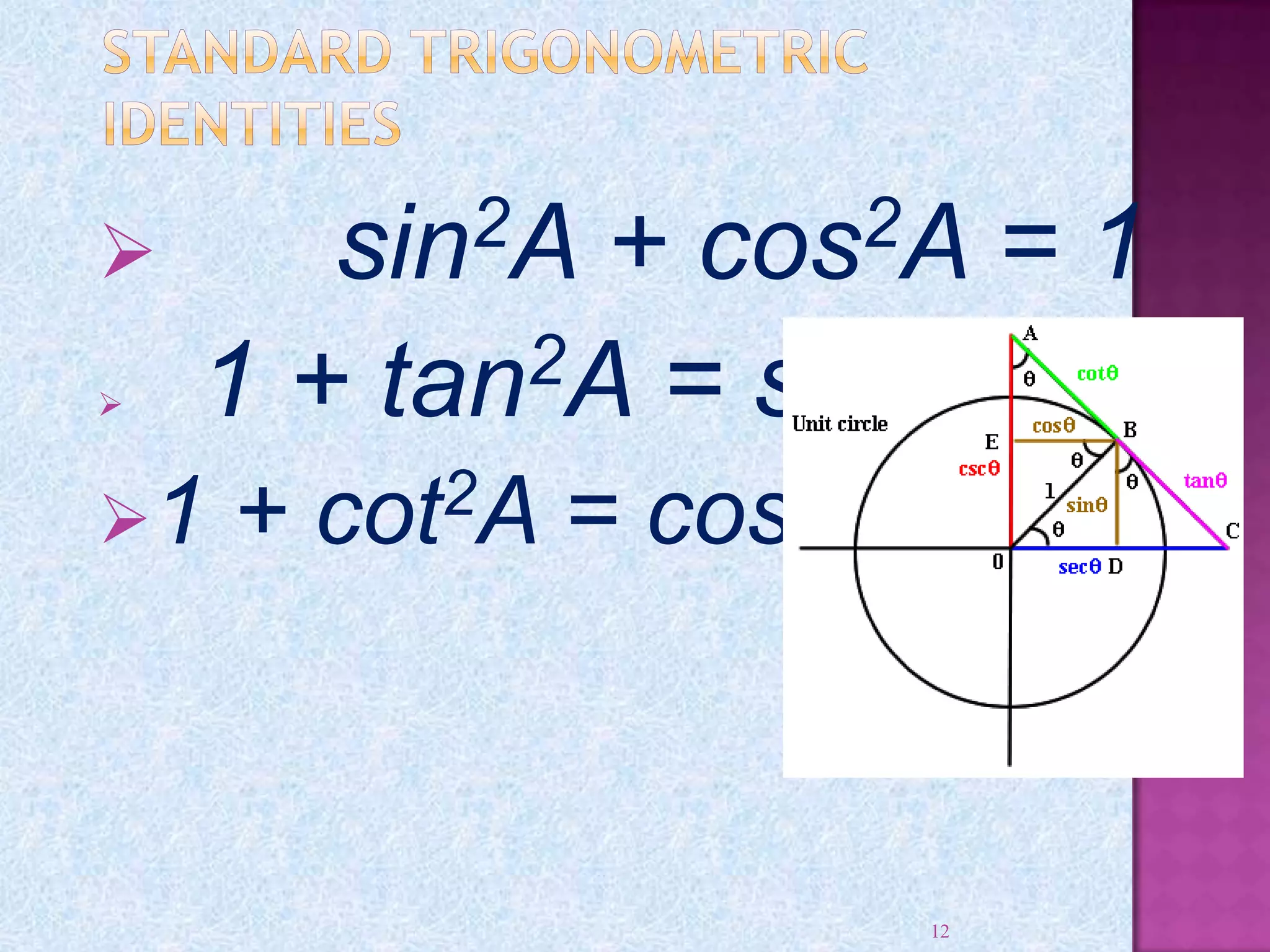
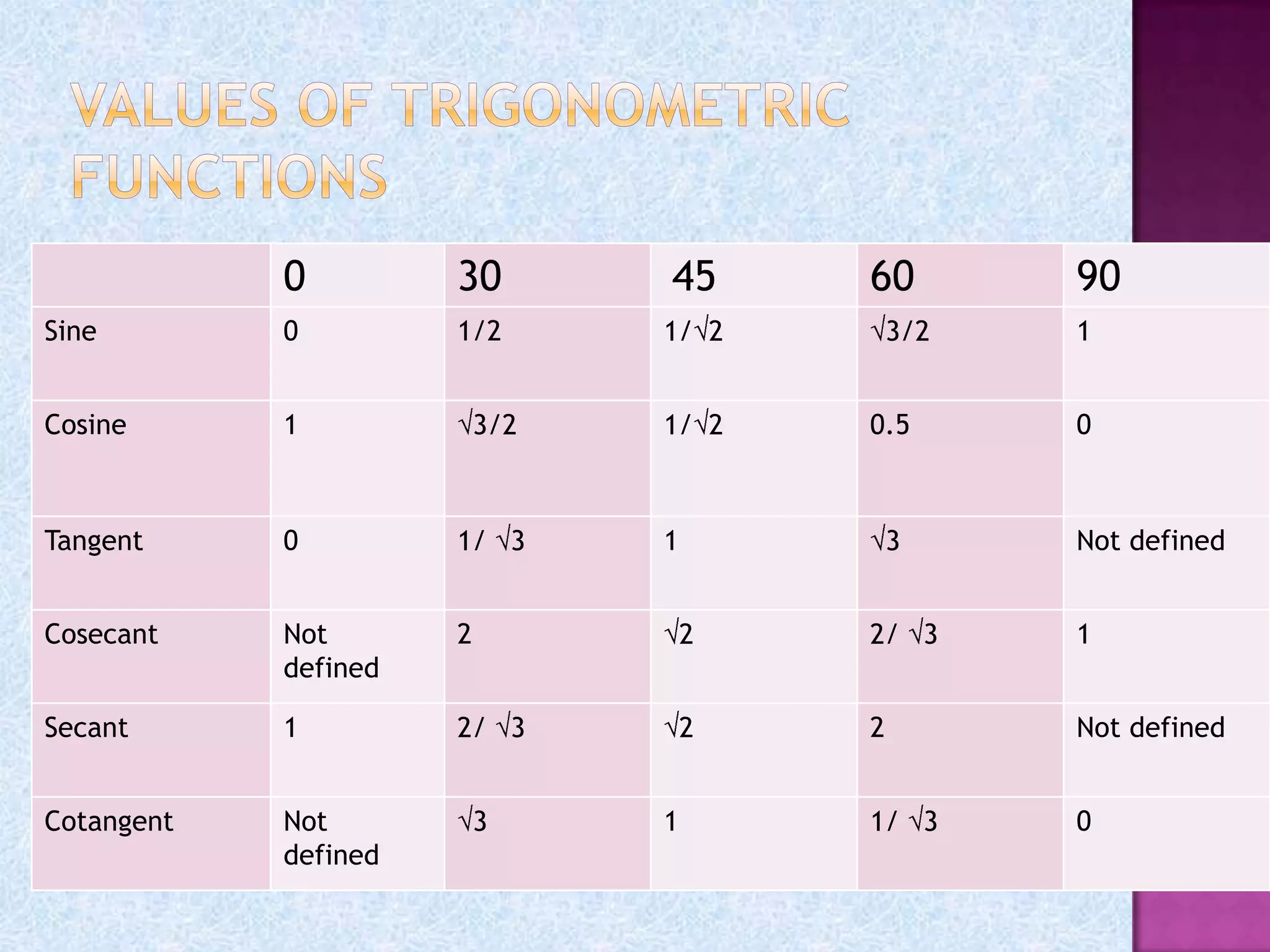
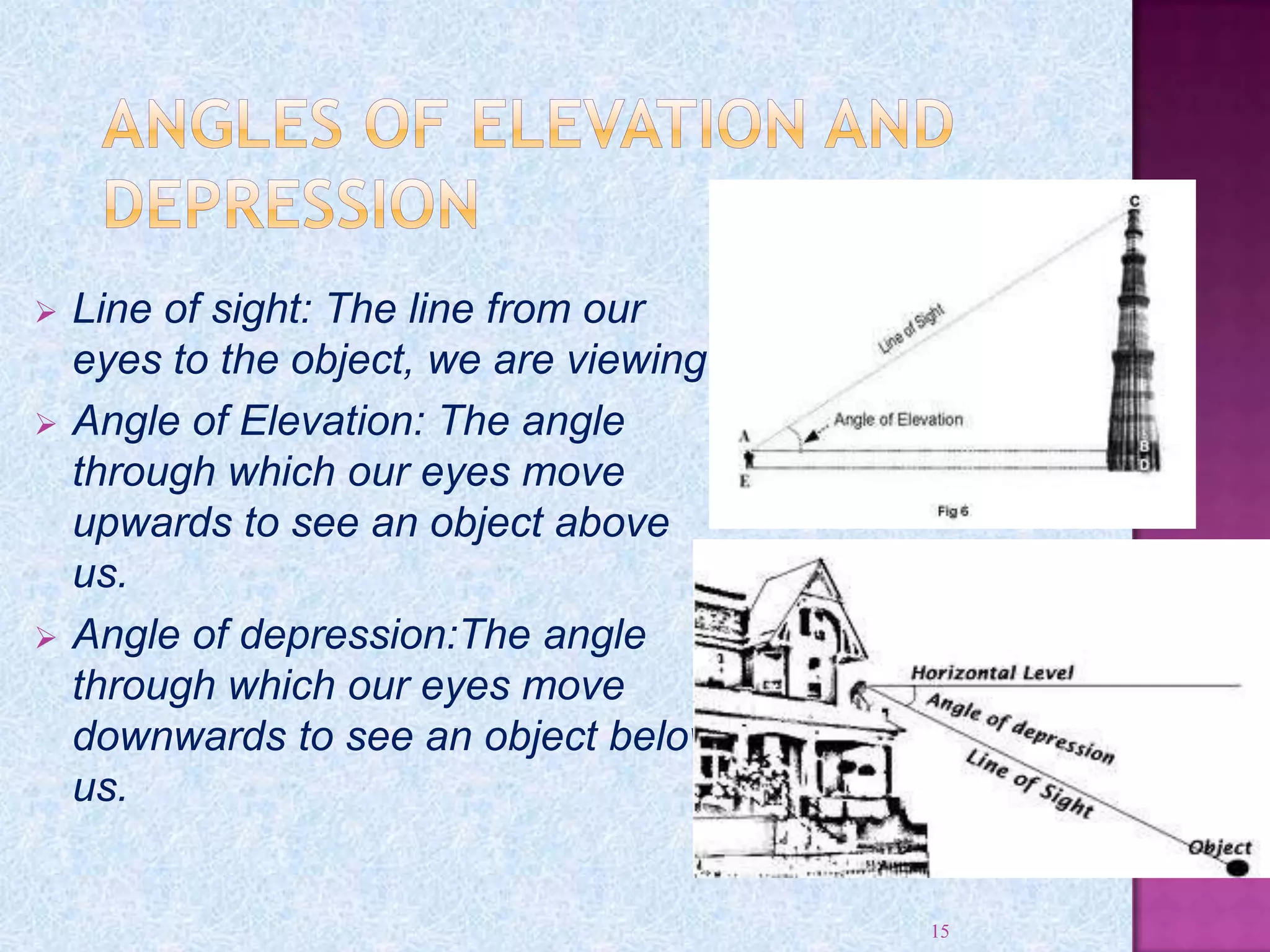
Kartikeya Pandey thanks his teacher Ms. Meha Bhargava and principal Ms. Jasleen Kaur for allowing him to complete a project on trigonometry. He also thanks his parents and friends for their help. The document then provides information on trigonometry including its origins in ancient mathematics, definitions of key terms like sine, cosine, and tangent. It also discusses right triangles, angle measurement in degrees and radians, trigonometric functions, trigonometric identities, and applications of trigonometry.

1. Kartikeya Pandey
10th Class – Section: A
Cambridge School Indirapuram
1

2. I would like to express my special thanks of
gratitude to my teacher Ms Meha Bhargava
as well as our principal Ms Jasleen Kaur who
gave me the golden opportunity to do this
wonderful project on the topic Trigonometry,
which also helped me in doing a lot of
Research and I came to know about so many
new things
I am really thankful to them.
Secondly I would also like to thank my
parents and friends who helped me a lot in
finishing this project within the limited time.
2

3.  Trigonometry is primarily a branch of
mathematics that deals with triangles,
mostly right triangles. In particular the
ratios and relationships between the
triangle's sides and angles. It has two
main ways of being used:in geometry
and analytically
3

4.  The complex origins of trigonometry are
embedded in the history of the simple
word "sine," a mistranslation of an Arabic
transliteration of a Sanskrit mathematical
term! The complex etymology of "sine"
reveals trigonometry's roots in Babylonian,
Greek, Hellenistic, Indian, and Arabic
mathematics and astronomy. Although
trigonometry now is usually taught
beginning with plane triangles, its origins
lie in the world of astronomy and spherical
triangles. Before the sixteenth century,
astronomy was based on the notion that
the earth stood at the center of a series of
nested spheres. To calculate the positions
of stars or planets, one needed to use 4

5.  A right triangle is a special
type of triangle in which one
angle is equal to 90
degrees.
 Although trigonometry can
be used in non right
triangles it mainly deals
with right triangles
5

6.  Degrees are used to express directionality
and angle size. If you stand facing directly
north, you are facing the direction of zero
degrees, written as 0 . If you turn yourself
fully around, so you end up facing north
again, you have "turned through" 360 ; that is,
one revolution (one circle) is 360 .
 1 degree = 60 minutes
 1 minute = 60 seconds
6

7.  The radian measure of an angle drawn in standard position
in the plane is equal to the length of arc on the unit circle
subtended by that angle.
In the figure, the angle drawn subtends an arc length of size
t on the unit circle so the radian measure of the angle is also
t. The symbol represents the real number constant which is
the ratio of the circumference of a circle to its diameter. Its
value is approximately 3.14159. Since the circumference of
the unit circle is 2 it follows that the radian measure of an
angle of one revolution is 2. The radian measure of an angle
whose terminal side is along the negative x -axis is .
7

8. 8
NAMES WRITTEN AS
Sine θ Sin θ
Cosine θ Cos θ
Tangent θ Tan θ
Cosecant θ Cosec θ
Secant θ Sec θ
Cotangent θ Cot θ

9. 9
Sin θ = reciprocal=
Cosec θ
Cos θ = reciprocal =
Sec θ
Tan θ = reciprocal =
Means :-
Sin θ = 1/
Cosec θ
(sin θ * cosec θ
= 1 )
Cos θ = 1/ Sec
θ
( cos θ * sec θ =
1 )

11. Sin ( 90° – θ ) = Cos θ
Cos ( 90° – θ ) = Sin θ
Tan ( 90° – θ ) = Cot θ
Cot ( 90° – θ ) = Tan θ
Cosec ( 90° – θ ) = Sec θ
Sec ( 90° – θ ) = Cosec θ
11

12.  sin2A + cos2A = 1
 1 + tan2A = sec2A
1 + cot2A = cosec2A
12

13. sin(A+B) = sinAcosB +
cosAsin B
cos(A+B) = cosAcosB –
sinAsinB
 sin2A =2sinAcosA
cos2A=cos2A - sin2A
13

14. 14
0 30 45 60 90
Sine 0 1/2 1/ 2 3/2 1
Cosine 1 3/2 1/ 2 0.5 0
Tangent 0 1/ 3 1 3 Not defined
Cosecant Not
defined
2 2 2/ 3 1
Secant 1 2/ 3 2 2 Not defined
Cotangent Not
defined
3 1 1/ 3 0

15.  Line of sight: The line from our
eyes to the object, we are viewing.
 Angle of Elevation: The angle
through which our eyes move
upwards to see an object above
us.
 Angle of depression:The angle
through which our eyes move
downwards to see an object below
us.
15

16. 16
Trigonometric tables were created over two
thousand years ago for computations in
astronomy. The stars were thought to be fixed on
a crystal sphere of great size, and that model was
perfect for practical purposes. Only the planets
moved on the sphere. (At the time there were
seven recognized planets: Mercury, Venus, Mars,
Jupiter, Saturn, the moon, and the sun. Those are
the planets that we name our days of the week
after. The earth wasn't yet considered to be a
planet since it was the center of the universe, and
the outer planets weren't discovered then.) The
kind of trigonometry needed to understand
positions on a sphere is called spherical
trigonometry. Spherical trigonometry is rarely

17.  Although trigonometry was first applied to spheres, it has had
greater application to planes. Surveyors have used trigonometry
for centuries. Engineers, both military engineers and otherwise,
have used trigonometry nearly as long. Physics lays heavy
demands on trigonometry. Optics and statics are two early fields
of physics that use trigonometry, but all branches of physics use
trigonometry since trigonometry aids in understanding space.
Related fields such as physical chemistry naturally use trig.
17

18. Of course, trigonometry is used throughout
mathematics, and, since mathematics is
applied throughout the natural and social
sciences, trigonometry has many applications.
Calculus, linear algebra, and statistics, in
particular, use trigonometry and have many
applications in the all the sciences.
18

19. Trigonometry is an important branch of mathematics.
The basics of trigonometry are used in every aspect
of our life. Trigonometry has resulted in many
remarkable discoveries which have changed the
human world
19