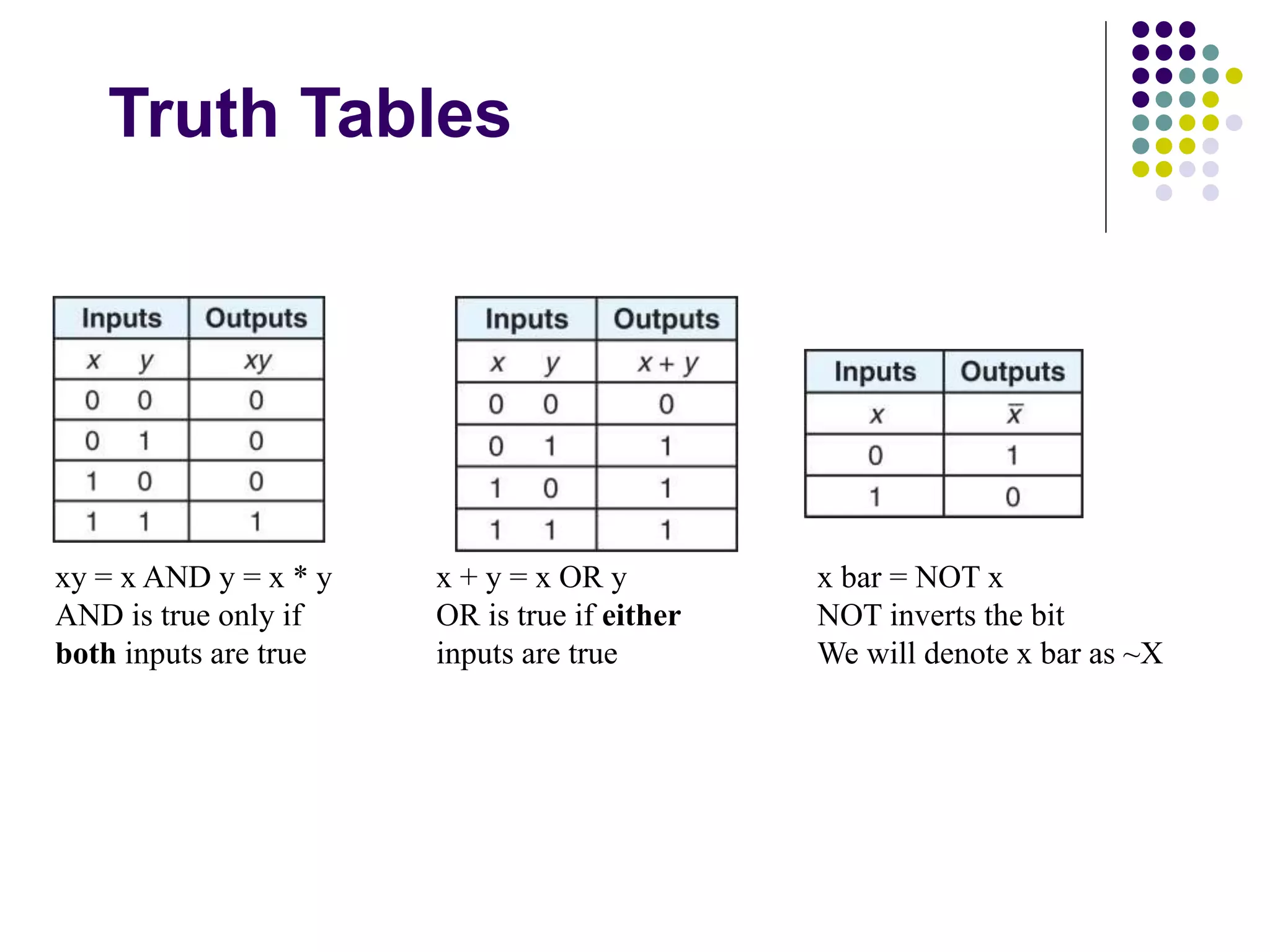
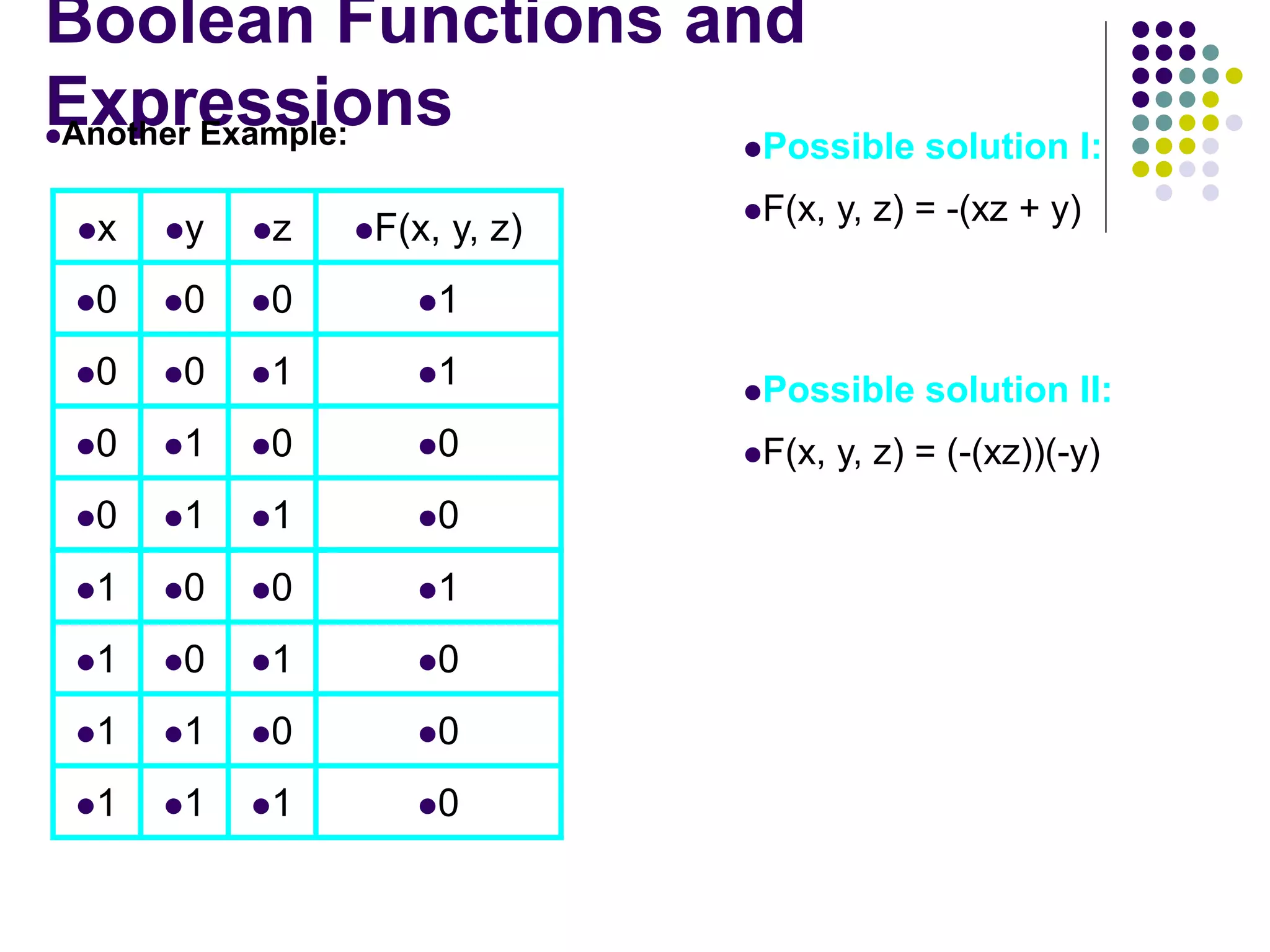
Boolean algebra is the algebra of binary values 0 and 1, also called false and true. The basic operations are AND, OR, and NOT. Boolean expressions represent Boolean functions and can be used to derive truth tables. Boolean algebra follows principles like duality, where operators are interchanged, and DeMorgan's laws, relating AND and OR operations on complements. Theorems prove identities like absorption and involution that simplify Boolean expressions.

1. BOOLEAN ALGEBRA

2. Boolean Algebra
 The basis for Boolean algebra:
 Boolean algebra is the algebra of binary values.
 we refer to these values as 0 and 1
 although we could also refer to them as true and false
 the basic Boolean algebra operations are
 AND, OR, NOT.

3. Basic Boolean Identities
 As with algebra, there will be Boolean
operations that we will want to simplify
 We apply the following Boolean identities to help
 For instance, in algebra, x = y * (z + 0) + (z * 0) can be
simplified to just x = y * z

5. Terminology
 Element 0 is called “FALSE”.
 Element 1 is called “TRUE”.
 ‘+’ operation “OR”,‘*’ operation “AND” and ’ operation “NOT”.
 Juxtaposition implies * operation: ab = a * b
 Operator order of precedence is: (), ’, *, +.
a+bc = a+(b*c) ≠ (a+b)*c
ab’ = a(b’) ≠ (a*b)’
 Single Bit Boolean Algebra(1’ = 0 and 0’ = 1)
+ 0 1
0 0 1
1 1 1
* 0 1
0 0 0
1 0 1

6. Truth Tables
xy = x AND y = x * y x + y = x OR y x bar = NOT x
AND is true only if OR is true if either NOT inverts the bit
both inputs are true inputs are true We will denote x bar as ~X

7. Boolean Functions and
Expressions
Definition: Let B = {0, 1}. The variable x is called
a Boolean variable if it assumes values only from
B.
A function from Bn, the set {(x1, x2, …, xn) |xiB,
1  i  n}, to B is called a Boolean function of
degree n.
Boolean functions can be represented using
expressions made up from the variables and
Boolean operations.

8. Boolean Functions and
Expressions
The Boolean expressions in the variables x1,
x2, …, xn are defined recursively as follows:
 0, 1, x1, x2, …, xn are Boolean expressions.
 If E1 and E2 are Boolean expressions, then (-
E1),
(E1E2), and (E1 + E2) are Boolean expressions.
Each Boolean expression represents a Boolean
function. The values of this function are obtained
by substituting 0 and 1 for the variables in the
expression.

9. Boolean Expressions
 We form Boolean expressions out of Boolean
operations on Boolean variables or Boolean values
 So, like algebraic expressions, we can create more
complex Boolean expressions as we might need
 Consider the expression:
 F = X + ~Y*Z
 What is it’s truth table?
Notice that it is easier to derive the
truth table for the entire expression
by breaking it into subexpressions
So first we determine ~Y
next, ~Y * Z
finally, X + ~Y*Z

10. Boolean Functions and
Expressions
Example: Give a Boolean expression for the
Boolean function F(x, y) as defined by the
following table:
x y F(x, y)
0 0 0
0 1 1
1 0 0
1 1 0
Possible solution: F(x, y) = (-x)y

11. Boolean Functions and
Expressions
Another Example: Possible solution I:
F(x, y, z) = -(xz + y)
0
0
1
1
F(x, y, z)
1
0
1
0
z
0
0
1
0
1
0
0
0
y
x
0
0
0
1
1
0
1
0
1
1
1
1
0
1
0
1
Possible solution II:
F(x, y, z) = (-(xz))(-y)

12. Duality
The dual of a Boolean expression is obtained by
interchanging Boolean sums and Boolean
products and interchanging 0s and 1s.
Examples:
The dual of x(y + z) is x +( yz)
The dual of -x1 + (-y + z) is (-x + 0)((-y)z).
The dual of a Boolean function F represented by a Boolean
expression is the function represented by the dual of this expression.

13. The dual of a statement S is obtained by interchanging * and +; 0
and 1.
Dual of (a*1)*(0+a’) = 0 is (a+0)+(1*a’) = 1
Dual of any theorem in a Boolean Algebra is also a theorem.
This is called the Principle of Duality.
Principle of Duality

14. Theorem 1
The complement of x is unique
Proof :
Assume x1' and x2' are both complements of x.
x + x1' = 1, x • x1' = 0, x + x2' = 1, x • x2' = 0
x1' = x1' • 1 1 is the identity for AND
= x1' • (x + x2') substitution, x + x2' = 1
= (x1' • x) + (x1' • x2') AND distributes over OR
= (x • x1') + (x1' • x2') AND is commutative
= 0 + (x1' • x2') substitution, x • x1' = 0
= (x • x2') + (x1' • x2') substitution, x • x2' = 0
= (x2' • x) + (x2' • x1') AND is commutative, twice
= x2' • (x + x1') AND distributes over OR
= x2' • 1 substitution, x + x1' = 1
= x2' 1 is the identity for AND
Thus, any two elements that are the complement of x are equal.
This implies that x' is unique

15. Theorem 2
x + 1 = 1
Proof:
x + 1 = 1 • (x + 1) 1 is the identity for AND
= (x + x') • (x + 1) Complement, x + x' = 1
= x + (x' • 1) OR distributes over AND
= x + x' 1 is the identity for AND
= 1 Complement, x + x' = 1
Theorem 3
AND's identity is the complement of OR's identity
0' = 1
Proof:
0' = 0 + 0' 0 is the identity for OR
= 1 Complement, x + x' = 1

16. Theorem 4
Idempotent
x + x = x
Proof:
x + x = (x + x) • 1 1 is the identity for AND
= (x + x) • (x + x') Complement, x + x' = 1
= x + (x • x') OR distributes over AND
= x + 0 Complement, x • x' = 0
= x 0 is the identity for OR

17. Theorem 5
Involution
(x')' = x
Proof:
Let x' be the complement of x and (x')' be the complement of x'.
x + x' = 1, xx' = 0, x' + (x')' = 1, and x'(x')' = 0
(x')' = (x')' + 0 0 is the identity for OR
= (x')' + xx' Substitution, xx' = 0
= [(x')' + x][(x')' + x'] OR distributes over AND
= [x + (x')'][x' + (x')'] OR is commutative (P3), twice
= [x + (x')'] • 1 Substitution, x' + (x')' = 1
= [x + (x')'][x + x'] Substitution, x + x' = 1
= x + [(x')' • x'] OR distributes over AND
= x + [x' • (x')'] AND is commutative
= x + 0 Substitution, x'(x')' = 0
= x 0 is the identity for OR

18. Theorem 6
Absorption
x + xy = x
Proof:
x + xy = (x • 1) + xy 1 is the identity for AND
= x(1 + y) AND distributes over OR
= x(y + 1) OR is commutative
= x • 1 x + 1 = 1 (Thm 2-1)
= x 1 is the identity for AND
Theorem 7
x + x'y = x + y
Proof:
x + x'y = (x + x') (x + y) OR distributes over AND
= 1 • (x + y) Complement x + x' = 1
= x + y 1 is the identity for AND

19. Theorem 8
DeMorgan's Law 1
(x + y)' = x' y'
Proof:
By Theorem 1 (complements are unique) and Postulate P9 (complement), for every x in a Boolean
algebra there is a unique x' such that
x + x' = 1 and x • x' = 0
So it is sufficient to show that x'y' is the complement of x + y. We'll do this by showing that (x + y)
+
(x'y') = 1 and (x + y) • (x'y') = 0
(x + y) + (x'y') = [(x + y) + x'] [(x + y) + y'] OR distributes over AND
= [(y + x) + x'] [(x + y) + y'] OR is commutative
= [y + (x + x')] [x + (y + y')] OR is associative,twice
= (y + 1)(x + 1) Complement, x + x' = 1, twice
= 1 • 1 x + 1 = 1 (Thm 2-1), twice
= 1 Idempotent, x • x = x (Thm 4-2)
Also,
(x + y)(x'y') = (x'y')(x + y) AND is commutative
= [(x'y')x] + [(x'y')y] AND distributes over OR
= [(y'x')x] + [(x'y')y] AND is commutative
= [y'(x'x)] + [x'(y'y)] AND is associative (Thm 8-2),twice
= [y'(xx')] + [x'(yy')] AND is commutative, twice
= [y' • 0] + [x' • 0] Complement, x • x' = 0, twice
= 0 + 0 x • 0 = 0 (Thm 2-2), twice
= 0 Idempotent, x + x = x (Thm 4-1)

20. Prove x + yz = (x + y)(x + z)
x + yz = (x + y)(x + z)
= xx + xz + xy + yz
= x + xz + xy + yz
= x (1 + z + y) + yz
= x (1) + yz
= x + yz
Prove (x + y) · (x + y') = x
x = (x + y) · (x + y')
= xx + xy + xy' + yy'
= x + xy + xy' + yy'
= x + xy + xy' + 0
= x (1 + y + y')
= x (1)
= x