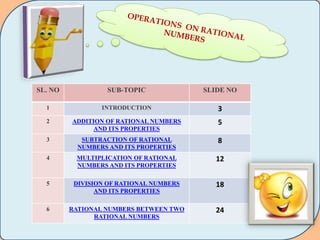
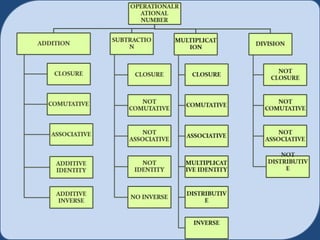
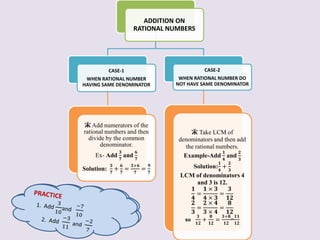
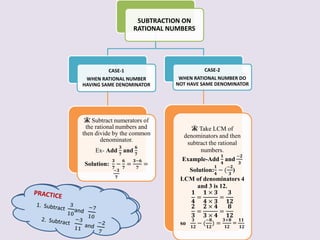
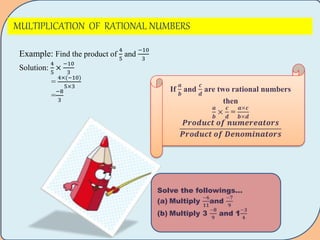
This document discusses properties of operations on rational numbers. It covers: 1) Addition of rational numbers, including having the same or different denominators. Properties include closure, commutativity, and additive identity. 2) Subtraction of rational numbers and its properties, noting the difference property and lack of an identity element. 3) Multiplication of rational numbers by multiplying numerators and denominators. Properties are closure, commutativity, associativity, identity of 1, and annihilation by 0. 4) Distributive property relating multiplication and addition/subtraction of rational numbers.

1. SL. NO SUB-TOPIC SLIDE NO
1 INTRODUCTION 3
2 ADDITION OF RATIONAL NUMBERS
AND ITS PROPERTIES
5
3 SUBTRACTION OF RATIONAL
NUMBERS AND ITS PROPERTIES
8
4 MULTIPLICATION OF RATIONAL
NUMBERS AND ITS PROPERTIES
12
5 DIVISION OF RATIONAL NUMBERS
AND ITS PROPERTIES
18
6 RATIONAL NUMBERS BETWEEN TWO
RATIONAL NUMBERS
24

2. INTRODUCTION
One day two children of Real number, Whole number and Rational
number have a talk with each other;
Whole number: Do you know rational ,different operations like
Addition,Subtraction ,MULTIPLICATION and DIVISION can act on me
and they also satisfies different properties.
Rational number: But brother I do not have any knowledge that how
these operations act on me. Let’s ask our teacher about this…
Teacher- I will definitely clear your doubts but
before that answer my questions…
 What is the additive identity for whole numbers ?
 Does whole number obeys commutative law under Subtraction ?
 What is the multiplicative inverse of 5 ?
 Define distributive property of Multiplication over Addition ?
 Say two whole numbers between 5 and 12 ?
 Tell whether division obeys closure property or not ?

3. The numbers of the form
𝒑
𝒒
,Where 𝒑 𝒂𝒏𝒅 𝒒 𝒂𝒓𝒆 𝒊𝒏𝒕𝒆𝒈𝒆𝒓𝒔 𝒂𝒏𝒅 𝒒 ≠ 𝒐 𝒂𝒓𝒆 𝒌𝒏𝒐𝒘𝒏 𝒂𝒔 𝒓𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝒏𝒖𝒎𝒃𝒆𝒓
Rational numbers include natural numbers, whole numbers, integer sand all positive and negative
fractions.
Example:
𝟓
𝟔
,
−𝟑
𝟖
, 𝟓
𝟐
𝟔
,… etc
Rational Numbers
As that of Whole numbers for rational numbers,also there are four operations they
are as following. Let’s discuss one after another…
 ADDITION
 SUBTRACTION
 MULTIPLICATION
 DIVISION

4. ADDITION ON
RATIONAL NUMBERS
CASE-1
WHEN RATIONAL NUMBER
HAVING SAME DENOMINATOR
Ӂ Add numerators of the
rational numbers and then
divide by the common
denominator.
Ex- Add
𝟑
𝟕
and
𝟔
𝟕
Solution:
𝟑
𝟕
+
𝟔
𝟕
=
𝟑+𝟔
𝟕
=
𝟗
𝟕
CASE-2
WHEN RATIONAL NUMBER DO
NOT HAVE SAME DENOMINATOR
Ӂ Take LCM of
denominators and then add
the rational numbers.
Example-Add
𝟏
𝟒
and
𝟐
𝟑
Solution:
𝟏
𝟒
+
𝟐
𝟑
LCM of denominators 4
and 3 is 12.
𝟏
𝟒
=
𝟏 × 𝟑
𝟒 × 𝟑
=
𝟑
𝟏𝟐
𝟐
𝟑
=
𝟐 × 𝟒
𝟑 × 𝟒
=
𝟖
𝟏𝟐
so
𝟑
𝟏𝟐
+
𝟖
𝟏𝟐
=
𝟑+𝟖
𝟏𝟐
=
𝟏𝟏
𝟏𝟐

5. PROPERTIES OF ADDITION OF RATIONAL NUMBERS
 Closure property:
Sum of any two rational number is always a rational number i.e if x and y are two rational numbers then x+y
will also became a rational number.
EXAMPLE :
1
2
+
3
4
=
5
4
Here
1
2
and
3
4
are both Rational number And sum
5
4
is also a rational number.
Hence Rational numbers are closed under Addition.
 Commutative property:
The sum of two rational numbers does not depend on the order in which they are added.i.e 𝑥 + 𝑦 = 𝑦 +
LHS=
𝟏
𝟐
+
𝟐
𝟑
+
𝟓
𝟒
=
𝟑+𝟒
𝟔
+
𝟓
𝟒
=
𝟕
𝟔
+
𝟓
𝟒
=
𝟏𝟒+𝟏𝟓
𝟏𝟐
=
𝟐𝟗
𝟏𝟐
RHS=
1
2
+
2
3
+
5
4
=
1
2
+
8+15
12
=
1
2
+
23
12
=
6+23
12
=
29
12

6.  Additive identity property:
When ‘o’ is added to any rational number the sum of the rational number is becomes
itself, If x is a rational number then 𝒙 + 𝟎 = 𝟎 + 𝒙 = 𝒙 .
EXAMPLE: let 𝑥 =
5
4
LHS=
5
4
+ 0 =
5
4
RHS=0 +
5
4
=
5
4
As LHS = RHS so this property valids.
Zero is called the identity element in Addition .
 Additive inverse property:
The negative of a rational number is it’s additive inverse.
The sum of a rational number and its additive inverse is always equal to Zero.
If x is a rational number then (-x) is the additive inverse of it and
𝑥 + −𝑥 = 0
Let a rational number be
5
4
𝑎𝑛𝑑 𝑖𝑡𝑠 𝑎𝑑𝑑𝑖𝑡𝑖𝑣𝑒 𝑖𝑛𝑣𝑒𝑟𝑠𝑒 𝑖𝑠
−5
4
Then
5
4
+
−5
4
=
5+ −5)
4
=
0
4
= 0
Negative of a rational number is called its additive inverse.
Try these—
(a) Simplify
−3
10
+
12
−10
+
14
10
(b) For x =
1
5
and y=
3
7
, verify that –(x+y) = (-x) + (-y)
(c) For x =
2
3
and y=
−5
6
and z=
7
9
, verify that (x+y)+ z = x + (y+z)

7. SUBTRACTION ON
RATIONAL NUMBERS
CASE-1
WHEN RATIONAL NUMBER
HAVING SAME DENOMINATOR
Ӂ Subtract numerators of
the rational numbers and
then divide by the common
denominator.
Ex- Add
𝟑
𝟕
and
𝟔
𝟕
Solution:
𝟑
𝟕
−
𝟔
𝟕
=
𝟑−𝟔
𝟕
=
−𝟑
𝟕
CASE-2
WHEN RATIONAL NUMBER DO
NOT HAVE SAME DENOMINATOR
Ӂ Take LCM of
denominators and then
subtract the rational
numbers.
Example-Add
𝟏
𝟒
and
−𝟐
𝟑
Solution:
𝟏
𝟒
−
−𝟐
𝟑
)
LCM of denominators 4
and 3 is 12.
𝟏
𝟒
=
𝟏 × 𝟑
𝟒 × 𝟑
=
𝟑
𝟏𝟐
𝟐
𝟑
=
𝟐 × 𝟒
𝟑 × 𝟒
=
𝟖
𝟏𝟐
so
𝟑
𝟏𝟐
−
−𝟖
𝟏𝟐
) =
𝟑+𝟖
𝟏𝟐
=
𝟏𝟏
𝟏𝟐

8. PROPERTIES OF SUBTRACTION OF RATIONAL NUMBERS
 EXAMPLE:
Difference of any two rational number is always a rational number i.e if x and y are two rational numbers then
x - y will also became a rational number.
VERIFICATION :
1
2
−
3
4
=
−1
4
Here
1
2
and
3
4
are both Rational numbers And their Difference
−1
4
is also
a rational number.
Hence Rational numbers are closed under Subtraction.
 PROPERTY-1:
The difference of two rational numbers does not remain same if their order is changed i.e 𝑥 − 𝑦) ≠
LHS=
𝟏
𝟐
−
𝟐
𝟑
-
𝟓
𝟒
=
𝟑−𝟒
𝟔
−
𝟓
𝟒
=
−𝟏
𝟔
+
𝟓
𝟒
=
−𝟐+𝟏𝟓
𝟏𝟐
=
𝟏𝟑
𝟏𝟐
RHS=
1
2
−
2
3
−
5
4
=
1
2
−
8−15
12
=
1
2
+
−7
12
=
6−7
12
=
−1
12

9.  EXAMPLE ;
For all rational number 𝒙 we have 𝒙 − 𝟎 = 𝒙 𝒃𝒖𝒕 𝟎 − 𝒙 = −𝒙
Show that,Ifx is a rational number then 𝒙 − 𝟎 ≠ 𝟎 − 𝒙 .
VERIFICATION: let 𝑥 =
5
4
LHS=
5
4
− 0 =
5
4
But RHS=0 −
5
4
=
−5
4
As LHS ≠ RHS so this property does not valid.
Identity element in Subtraction does not exist .
 EXAMPLE:
Since identity of subtraction does not exist so inverse for Subtraction does
not arise.
Try thesee—
(a) Simplify
−3
10
−
12
−10
−
14
10
(b) For x =
2
3
and y=
−5
6
and z=
7
9
, verify that (x-y)-z = x –(y-z)

10. MULTIPLICATION OF RATIONAL NUMBERS
Example: Find the product of
4
5
and
−10
3
Solution:
4
5
×
−10
3
=
4× −10)
5×3
=
−8
3
If
𝒂
𝒃
and
𝒄
𝒅
are two rational numbers
then
𝒂
𝒃
×
𝒄
𝒅
=
𝒂×𝒄
𝒃×𝒅
𝑷𝒓𝒐𝒅𝒖𝒄𝒕 𝒐𝒇 𝒏𝒖𝒎𝒆𝒓𝒆𝒂𝒕𝒐𝒓𝒔
𝑷𝒓𝒐𝒅𝒖𝒄𝒕 𝒐𝒇 𝑫𝒆𝒏𝒐𝒎𝒊𝒏𝒂𝒕𝒐𝒓𝒔
Solve the followings…
(a) Multiply
−𝟔
𝟏𝟏
and
−𝟕
𝟗
(b) Multiply 3
−𝟖
𝟗
and 1
−𝟑
𝟒

11. PROPERTIES OF MULTIPLICATION OF RATIONAL NUMBERS
 CLOSURE PROPERTY:
Product of any two rational number is always a rational number
EXAMPLE:
1
2
×
3
4
=
3
8
Here
1
2
and
3
4
are both Rational number And product
3
8
are rational number
Hence Rational numbers are closed under multiplication.
 COMMUTATIVE PROPERTY:
The product of two rational numbers remain same even if we change their
order . If 𝑥 and 𝑦 are two rational number then 𝑥 × 𝑦 = 𝑦 × 𝑥
Example: Verify that product of two rational number
−2
7
and
1
4
remains same
even if the order is changed .
LHS=
−2
7
×
1
4
=
−1
14
Hence LHS=RHS
RHS=
1
4
×
−2
7
=
−1
14
Commutative property holds TRUE in multiplication of rational number.

12.  Associative Property:
The product of three rational numbers remains same even after
changing the groups.
If x , y, z are three rational numbers then 𝑥 × 𝑦) × 𝑧 = 𝑥 × 𝑦 × 𝑧
Example: Verify that product of three rational numbers
−3
4
,
5
7
and
−2
11
remains same
even after changing the groupings.
LHS=
−3
4
×
5
7
×
−2
11
=
−15
28
×
−2
11
=
15
154
RHS=
−3
4
×
5
7
×
−2
11
=
−3
4
×
−10
77
=
15
154
LHS=RHS

13.  MULTIPLICATIVE IDENTITY:
When 1 is multiplied to any rational number then the product of the rational
number is equal to itself
If x is a rational number then 𝑥 × 1 = 1 × 𝑥 = 𝑥
Example: let 𝑥 =
5
4
LHS=
5
4
× 1 =
5
4
RHS=1 ×
5
4
=
5
4
Hence LHS = RHS
1 is the identity element under the multiplication
 PRODUCT OF A RATIONAL NUMBER AND ZERO IS ALWAYS
ZERO
If 𝑥 𝑖𝑠 𝑎𝑛𝑦 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑡ℎ𝑒𝑛 𝑥 × 0 = 0 × 𝑥 = 0
EXAMPLE: The product of
−4
7
𝑎𝑛𝑑 0
−4
7
× 0 =
−4×0
7×1
=
0
7
= 0
Again 0 ×
−4
7
=
0×−4
1×7
=
0
7
= 0

14. Distributive property:
If 𝑥, 𝑦𝑎𝑛𝑑 𝑧 𝑎𝑟𝑒 𝑡ℎ𝑒 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠 𝑡ℎ𝑒𝑛
i)𝑥 × 𝑦 + 𝑧 = 𝑥 × 𝑦) + 𝑥 × 𝑧)
(ii) 𝑥 × 𝑦 − 𝑧 = 𝑥 × 𝑦) − 𝑥 × 𝑧)
Example: For three rational number𝑥 =
5
6
, 𝑦 =
−7
3
, 𝑧 =
2
9
𝑡ℎ𝑒𝑛 𝑣𝑒𝑟𝑖𝑓𝑦 𝑡ℎ𝑎𝑡
LHS = 𝑥 × 𝑦 − 𝑧
=
5
6
×
−7
3
−
2
9
=
5
6
×
−21−2
9
=
5× −23)
6×9
=
−115
54
RHS= (𝑥 × 𝑦) − 𝑥 × 𝑧)
=
5
3
×
−7
3
−
5
6
×
2
9
=
−35
18
−
10
54
=
−105−10
54
=
−115
54
LHS=RHS Hence verified…
So Rational numbers obeys Distributive property of multiplication over
Addition and Subtraction.

15.  Reciprocal of a rational number(Multiplicative Inverse)
Reciprocal of rational number means interchanging of numerator and
denominator in other words Rational number obtained after inverting the
given rational number is called Reciprocal of rational number
Example : The Reciprocal of
9
4
is
4
9
Note:
(1)Zero has no Reciprocal
(ii)Reciprocal of 1 is 1
(iii) if x is any non zero rational number,then its
reciprocal is denoted by 𝑥−1
which is equal to
1
𝑥

16. DIVISION OF RATIONAL NUMBERS
EXAMPLE: Divide
7
3
𝑏𝑦
5
3
Solution :
7
3
÷
5
3
=
7
3
×
5
3
−1
𝑥 ÷ 𝑦 = 𝑥 × 𝑦−1
=
7
3
×
3
5
=
7
5
Dividing one rational number by
another except by zero, is the same
as the multiplication of the first by
the reciprocal of the second,
i.ex÷y = x×y-1
Divide followings…
(a) -10 by
1
5
(b)
1
13
by -2

17. PROPORTIES OF DIVISION OF RATIONAL NUMBER
Property: 1
Divisionof a rational number by another rational number except zero is always
rational number.
Example: (i)
5
3
−
4
3
=
5
3
×
3
−4
=
−5
4
(ii) 0 ÷
−4
5
= 0
(iii)
−4
5
÷ 0 =
−4
5
×
1
0
=
−4
0
𝑤ℎ𝑖𝑐ℎ 𝑖𝑠 𝑛𝑜𝑡 𝑎 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟)
Property-2
When a nonzero rational number divided by itself we get always 1
Example :
3
4
÷
3
4
=
3
4
×
4
3
= 1
Property-3
When non zero rational number divided by 1 the quotient is
the same rational number
Example
−4
5
÷ 1 =
−4
5
×
1
1
=
−4
5

18. PROPERTY-4
The division of two rational number does not remain same if
the order of the number are changed.
If 𝑥 𝑎𝑛𝑑 𝑦 are two rational number then 𝑥 ÷ 𝑦 ≠ 𝑦 ÷ 𝑥
Example:Verify that if 𝑥 =
2
3
and 𝑦 =
−4
5
then 𝑥 ÷ 𝑦 ≠ 𝑦 ÷ 𝑥
• LHS=𝑥 ÷ 𝑦
=
3
2
÷
−4
5
=
3
2
×
5
−4
=
−15
8
• RHS=𝑦 ÷ 𝑥
=
−4
5
÷
3
2
=
−4
5
×
2
3
=
−8
15
LHS≠RHS
H𝑒𝑛𝑐𝑒 𝑐𝑜𝑢𝑚𝑢𝑡𝑎𝑡𝑎𝑖𝑣𝑒 𝑝𝑟𝑜𝑝𝑒𝑟𝑡𝑦 𝑑𝑜𝑒𝑠𝑛𝑜𝑡 ℎ𝑜𝑙𝑑 𝑡𝑟𝑢𝑒 𝑓𝑜𝑟 𝑑𝑖𝑣𝑖𝑠𝑖𝑜𝑛

19. PROPERTY-5
The division of three rational numbers does not remains same even after
changing the groups.
If x , y, z are three rational numbers then 𝑥 ÷ 𝑦) ÷ 𝑧 ≠ 𝑥 ÷ 𝑦 ÷ 𝑧
Example:Verify that if 𝑥 =
2
3
, 𝑦 =
−4
9
,𝑧 =
5
6
then 𝑥 ÷ 𝑦) ÷ 𝑧 ≠ 𝑥 ÷ 𝑦 ÷ 𝑧
• LHS= 𝑥 ÷ 𝑦) ÷ 𝑧
=
2
3
÷
−4
9
÷
5
6
=
−3
2
÷
5
6
=
−3
2
×
6
5
=
−9
5
• RHS=𝑥 ÷ 𝑦 ÷ 𝑧)
=
2
3
÷
−4
9
÷
5
6
=
2
3
÷
−8
15
=
2
3
×
15
−8
=
−5
4
LHS≠RHS
Associative property does not holds true for division

20. PROPERTY-6:
If 𝒙, 𝒚 𝒂𝒏𝒅 𝒛 are rational numbers, then
𝒙 + 𝒚 ÷ 𝒛 = 𝒙 ÷ 𝒛) + 𝒚 ÷ 𝒛) and 𝒙 − 𝒚 ÷ 𝒛 =
𝒙 ÷ 𝒛 − 𝒚 ÷ 𝒛)
Example : If 𝒙 =
−𝟐
𝟑
, 𝒚 =
𝟓
𝟗
, 𝒛 =
−𝟏
𝟔
𝒕𝒉𝒆𝒏 𝒔𝒉𝒐𝒘 𝒕𝒉𝒂𝒕
𝒙 + 𝒚 ÷ 𝒛 = 𝒙 ÷ 𝒛 + 𝒚 ÷ 𝒛
LHS = 𝑥 + 𝑦 ÷ 𝑧
=
−2
3
+
5
9
÷
−1
6
=
−6+5
9
÷
−1
6
=
−1
9
÷
−1)
6
=
−1
9
×
6
−1
=
2
3
RHS = 𝑥 ÷ 𝑧) + 𝑦 ÷ 𝑧)
=
−2
3
÷
−1)
6
+
5
9
÷
−1)
6
=
−2
3
×
6
−1)
+
5
9
×
6
−1)
= 4 −
5×2
3
=
4
1
−
10
3
=
12−10
3
=
2
3
LHS = RHS

21. PROPERTY- 7
For three non-zero rational numbers 𝒙, 𝒚 𝒂𝒏𝒅 𝒛,
𝒙 ÷ 𝒚 + 𝒛 ≠ 𝒙 ÷ 𝒚 + 𝒙 ÷ 𝒛
Example :- If 𝒙 =
𝟐
𝟓
, 𝒚 =
−𝟑
𝟏𝟎
, 𝒛 =
𝟒
𝟏𝟓
show that
𝒙 ÷ 𝒚 + 𝒛 ≠ 𝒙 ÷ 𝒚 + 𝒙 ÷ 𝒛
• LHS=𝑥 ÷ 𝑦 + 𝑧
=
2
5
÷
−3
10
+
4
15
=
2
5
÷
−9+8
30
=
2
5
÷
−1
30
=
2
5
×
30
−1
= −2 × 6 = −12
• RHS=𝑥 ÷ 𝑦 + 𝑥 ÷ 𝑧
=
2
5
÷
−3
10
+
2
5
÷
4
15
=
2
5
×
10
−3
+
2
5
×
15
4
=
−2×2
3
+
1×3
1×2
=
−4
3
+
3
2
=
−8+9
6
=
1
6
LHS ≠ RHS
Distributive property does not hold true for division

22. RATIONALS BETWEEN TWO RATIONAL NUMBERS
Example: Find two rational number between
1
2
𝑎𝑛𝑑
−1
2
Solution: Step-1 Find a rational number between
1
2
𝑎𝑛𝑑
−1
2
1
2
×
1
2
+
−1
2
=
1
2
× 0 = 0
Step-2 Find a rational number between
1
2
𝑎𝑛𝑑 0
1
2
×
1
2
+ 0 =
1
2
×
1
2
=
1
4
Hence 0,
1
4
are two rational number between
1
2
𝑎𝑛𝑑
−1
2
If 𝒙 𝒂𝒏𝒅𝒚 𝒂𝒓𝒆 𝒕𝒘𝒐 𝒓𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝒏𝒖𝒎𝒃𝒆𝒓𝒔 , 𝒕𝒉𝒆𝒏
𝒙+𝒚
𝟐
𝒊𝒔 𝒂
𝒓𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝒏𝒖𝒎𝒃𝒆𝒓 𝒃𝒆𝒕𝒘𝒆𝒆𝒏 𝒙 𝒂𝒏𝒅 𝒚.

23. Introduction of Rational number
Operation of rational number
Properties of addition of rational number
Properties of subtraction of rational number
Properties of Multiplication of rational
number
Properties of division of rational number
Insert rational numbers between two given
rational number
KEY POINTS