Recommended
Recommended
More Related Content
Similar to AIOU Code 1349 Solved Assignment 2 Autumn 2022.pptx
Similar to AIOU Code 1349 Solved Assignment 2 Autumn 2022.pptx (20)
More from Zawarali786
More from Zawarali786 (20)
Recently uploaded
Recently uploaded (20)
AIOU Code 1349 Solved Assignment 2 Autumn 2022.pptx
- 1. Course: Introduction to Business Mathematics (1349) Semester: Autumn, 2022 ASSIGNMENT No. 2 Q. 1 (a) Find the inverse of the given matrix: 2 1 2 3 0 3 1 4 5 0314-4646739 0336-4646739 Skilling.pk Diya.pk 1 Stamflay.com 0332-4646739
- 4. (b) Define even and odd functions with examples. Decide whether the equation x2 + y2 = 1 is a function? Explain. There are different types of functions in mathematics that we study. We can determine whether a function is even or odd algebraically or graphically. Even and Odd functions can be checked by plugging in the negative inputs (-x) in place of x into the function f(x) 0314-4646739 Skilling.pk Diya.pk 4 Stamflay.com 0336-4646739 0332-4646739
- 5. and considering the corresponding output value. Even and odd functions are classified on the basis of their symmetry relations. Even and odd functions are named based on the fact that the power function f(x) = xn is an even function, if n is even, and f(x) is an odd function if n is odd. Generally, we consider a real-valued function to be even or odd. To identify if a function is even or odd, we plug in -x in place of x into the function f(x), that is, we check the output value of f(-x) to determine the type of the function. Even and odd functions are symmetrical. Let us first understand their definitions. Even and Odd Functions Definition Even Function - For a real-valued function f(x), when the output value of f(-x) is the same as f(x), for all values of x in the domain of f, the function is said to be 0314-4646739 0336-4646739 0332-4646739 Skilling.pk Diya.pk 5 Stamflay.com
- 6. an even function. An even function should hold the following equation: f(-x) = f(x), for all values of x in D(f), where D(f) denotes the domain of the function f. In other words, we can say that the equation f(-x) - f(x) = 0 holds for an even function, for all x. Let us consider an example, f(x) = x2. f(-x) = (-x)2 = x2 for all values of x, as the square of a negative number is the same as the square of the positive value of the number. This implies f(-x) = f(x), for all x. Hence, f(x) = x2 is an even function. Similarly, functions like x4, x6, x8, etc. are even functions. Odd Function - For a real-valued function f(x), when the output value of f(-x) is the same as the negative of f(x), for all values of x in the domain of f, the function is said to be an odd function. An odd function should hold the following equation: 0314-4646739 0336-4646739 0332-4646739 Skilling.pk Diya.pk 6 Stamflay.com
- 7. f(-x) = -f(x), for all values of x in D(f), where D(f) denotes the domain of the function f. In other words, we can say that the equation f(-x) + f(x) = 0 holds for an odd function, for all x. Let us consider an example, f(x) = x3. f(-x) = (-x)3 = -(x3) for all values of x, as the cube of a negative number is the same as the negative of the cube of the positive value of the number. This implies f(-x) = -f(x), for all x. Hence, f(x) = x3 is an odd function. Similarly, functions like x5, x7, x9 etc. are odd functions. Both Even and Odd Functions - A real-valued function f(x) is said to be both even and odd if it satisifies f(-x) = f(x) and f(-x) = -f(x) for all values of x in the domain of the function f(x). There is only one function which is both even and odd and that is the zero function, f(x) = 0 for all x. We know that for zero function, 0314-4646739 0336-4646739 0332-4646739 Skilling.pk Diya.pk 7 Stamflay.com
- 8. f(-x) = -f(x) = f(x) = 0, for all values of x. Hence, f(x) = 0 is an even and odd function. Neither Even Nor Odd Function - A real-valued function f(x) is said to be neither even nor odd if it does not satisfy f(-x) = f(x) and f(-x) = -f(x) for atleast one value of x in the domain of the function f(x). Let us consider an example to understand the definition better. Consider f(x) = 2x5 + 3x2 + 1, f(-x) = 2(-x)5 + 3(-x)2 + 1 = - 2x5 + 3x2 + 1 which is neither equal to f(x) nor -f(x). Hence, f(x) = 2x5 + 3x2 + 1 is neither even nor odd function. In the first quadrant (where x and y coordinates are all positive), all six trigonometric ratios have positive values. In the second quadrant, only sine and cosecant are positive. In the third quadrant, only tangent and cotangent are positive. In the fourth quadrant, only 0314-4646739 0336-4646739 0332-4646739 Skilling.pk Diya.pk 8 Stamflay.com
- 9. cosine and secant are positive. Based on these signs, we will categorize them as even and odd functions. If a trigonometric ratio is even or odd can be checked through a unit circle. An angle measured in anticlockwise direction is a positive angle whereas the angle measured in the clockwise direction is a negative angle. The graph of an even function is symmetric with respect to the y-axis. In other words, the graph of an even function remains the same after reflection about the y-axis. For any 0314-4646739 0336-4646739 0332-4646739 Skilling.pk Diya.pk 9 Stamflay.com
- 10. two opposite input values of x, the function value will remain the same all along the curve. Whereas the graph of an odd function is symmetric with respect to the origin. In other words, the graph of an odd function is at the same distance from the origin but in opposite directions. For any two opposite input values of x, the function has opposite y values. Here are a few examples of even and odd functions. 0314-4646739 0336-4646739 0332-4646739 Skilling.pk Diya.pk 10 Stamflay.com
- 11. The graph of an even function is symmetric with respect to the y-axis. In other words, the graph of an even function remains the same after reflection about the y-axis. For any two opposite input values of x, the function value will remain the same all along the curve. 0314-4646739 Skilling.pk Diya.pk 11 Stamflay.com 0336-4646739 0332-4646739
- 12. Whereas the graph of an odd function is symmetric with respect to the origin. In other words, the graph of an odd function is at the same distance from the origin but in opposite directions. For any two opposite input values of x, the function has opposite y values. Here are a few examples of even and odd functions. 0314-4646739 0336-4646739 0332-4646739 Skilling.pk Diya.pk 12 Stamflay.com
- 13. x 3 f (x) x . (c) Find the domain of the function Interval Notation: (−∞,3)∪(3,∞)(-∞,3)∪(3,∞) 0314-4646739 Skilling.pk Diya.pk 13 Stamflay.com 0336-4646739 0332-4646739
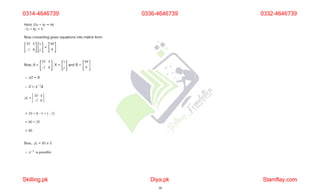
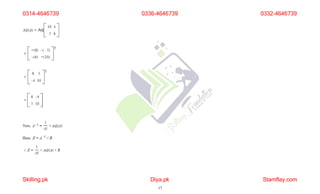
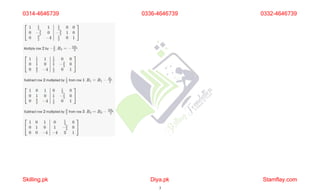
- 14. Set-Builder Notation: {x|x≠3} Q. 2 (a) If A is a square matrix, then show that A +At is symmetric. Let B=A+AT. Now, BT =(A+AT)T =AT+(AT)T =AT+A [ Since (AT)T=A] =B. So, A+AT is a symmetric matrix. 0314-4646739 Skilling.pk Diya.pk 14 Stamflay.com 0336-4646739 0332-4646739
- 15. (b) Determine the solution of the system of equations by (i) Matrix method (ii) Cramer’s rule: 10x1 + 4x2 = 46 –5x1 + 6x2 = 9 Let x1 = x x2 = y 0314-4646739 Skilling.pk Diya.pk 15 Stamflay.com 0336-4646739 0332-4646739
- 18. By Cramers Rule 0314-4646739 Skilling.pk Diya.pk 18 Stamflay.com 0336-4646739 0332-4646739
- 21. Q. 3 (a) Find the solution of the given equation by factorization and completing square method. x2 – 8x + 15 = 0 By Factorization x2 – 5x – 3x + 15 = 0 x (x – 5) – 3 (x – 5) = 0 (x – 3) (x – 5) = 0 X = 3, 5 By Completing Square Method x2 – 8x + 15 = 0 0314-4646739 0336-4646739 0332-4646739 Skilling.pk Diya.pk 21 Stamflay.com
- 23. (b) Solve the equation: 2 1 x3 2x3 8 0 0314-4646739 Skilling.pk Diya.pk 23 Stamflay.com 0336-4646739 0332-4646739
- 26. Q. 4 (a) Find two numbers whose sum and product are 14 and 45 respectively. 0314-4646739 Skilling.pk Diya.pk 26 Stamflay.com 0336-4646739 0332-4646739
- 28. (b) Find the market equilibrium point for the following supply and demand functions: Demand: P = –3q + 26 Supply: P = 4q – 9 Demand = Supply –3q + 26 = 4q – 9 -3q – 4q = -26 – 9 -7q = -33 q = 33 / 7 = 4.71 p = -3(33/7) + 26 p = -99/7 + 26 0314-4646739 0336-4646739 0332-4646739 Skilling.pk Diya.pk 28 Stamflay.com
- 29. p = -14.14 + 26 = 12 p = 11.9 (c)Find the x and y intercept if: y = x2 – 2x – 8 Let x = 0 Y = -8 y-intercept = (0, -8) Let y = 0 0 = x2 – 2x – 8 x2 – 2x – 8 = 0 x2 – 4x + 2x – 8 = 0 0314-4646739 Skilling.pk Diya.pk 29 Stamflay.com 0336-4646739 0332-4646739
- 30. x (x-4) + 2(x-4) = 0 (x-4) (x+2) = 0 X = 4, -2 X intercept = (4,0) and (-2, 0) List the intersections. x-intercept(s): (4,0) ,(-2,0) y-intercept(s): (0, −8) Q. 5 (a) Simplify the following in binary system: i) {[10001101)2 x (2335)10} – (278)10 = {[10001101)2 x (100100011111)2} - (100010110)2 First First we will solve [10001101)2 x (100100011111)2} 0314-4646739 Skilling.pk Diya.pk 30 Stamflay.com 0336-4646739 0332-4646739
- 32. Now, =(1 0 1 0 0 0 0 0 1 1 0 0 0 0 1 0 0 1 1 )2 - (100010110)2 ii) {[11011101)2 ÷ (134)10} x (1011101)2 Converting (134)10 into decimal we get (10000110)2 Now we need to solve, {[11011101)2 ÷ (134)10} 0314-4646739 0336-4646739 Skilling.pk Diya.pk 32 Stamflay.com 0332-4646739
- 34. =( 1.10100110001101011)2 x (1011101)2 0314-4646739 0336-4646739 Skilling.pk Diya.pk 34 Stamflay.com 0332-4646739
- 35. b) Evaluate the following: i) (10001111.101)2 – (1101011)2 ii) (10101.101)2 x (1011.011)2 0314-4646739 Skilling.pk Diya.pk 35 Stamflay.com 0336-4646739 0332-4646739