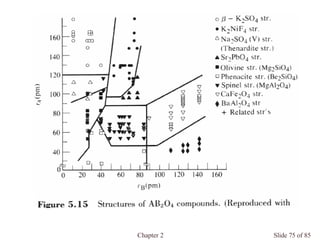
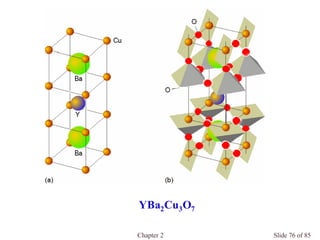
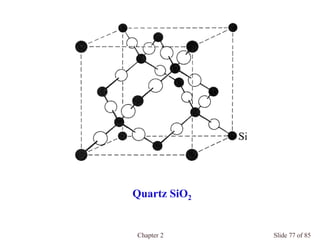
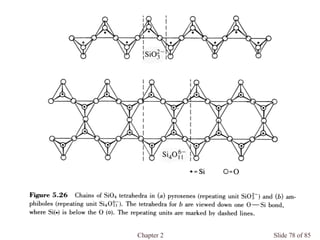
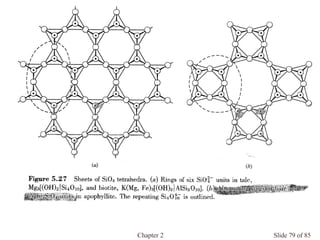
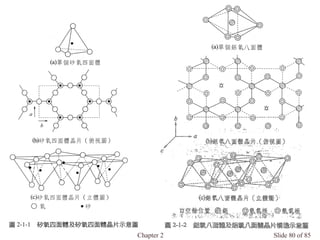
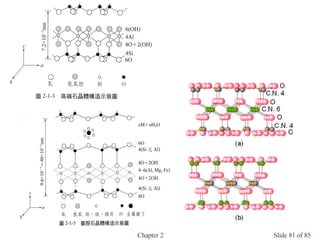
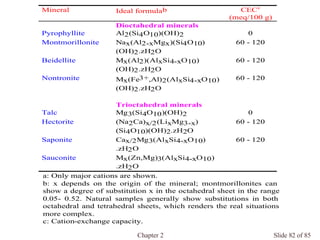
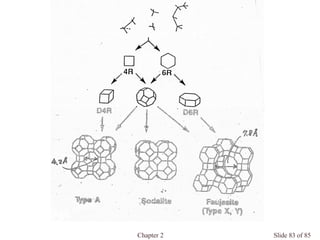
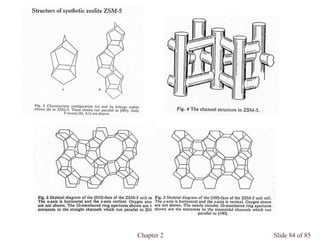
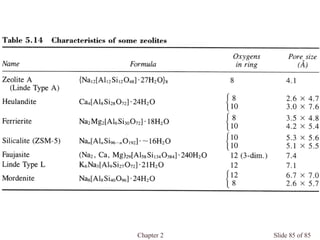
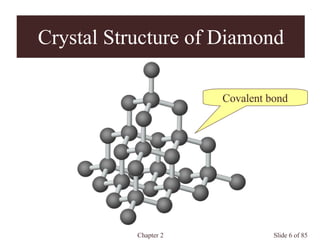
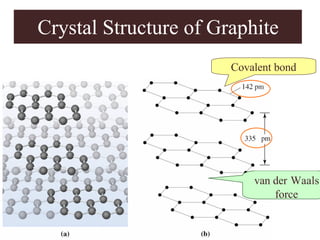
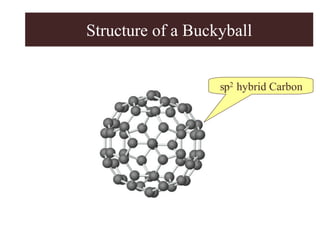
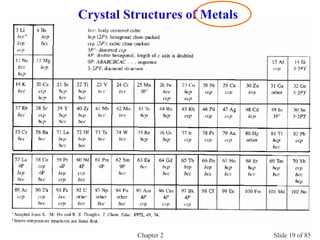
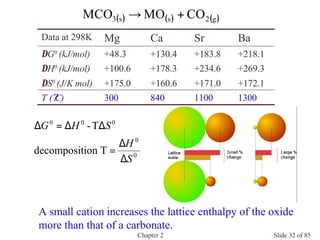
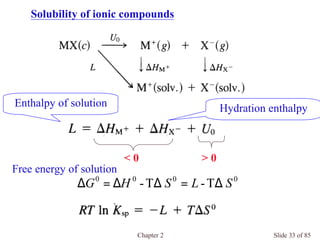
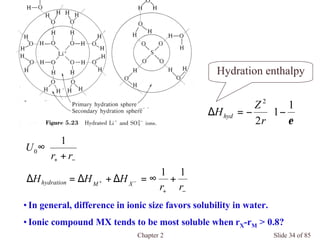
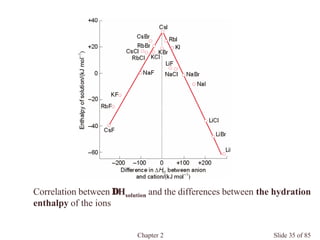
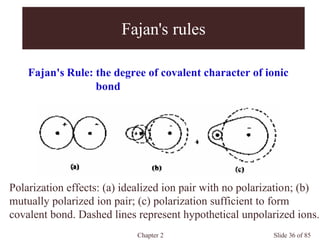
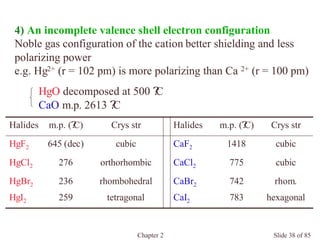
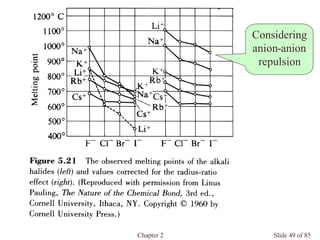
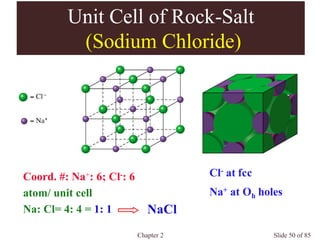
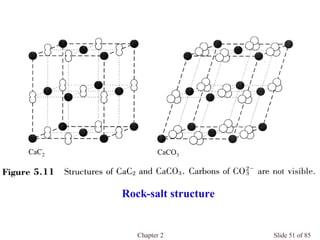
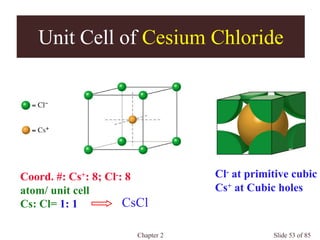
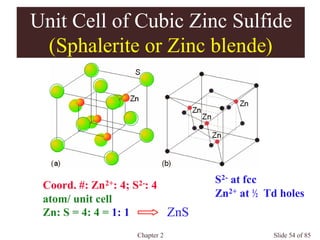
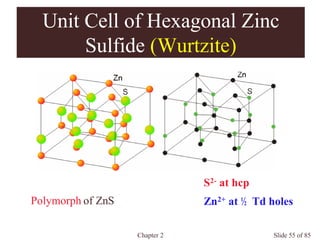
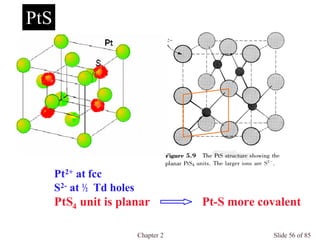
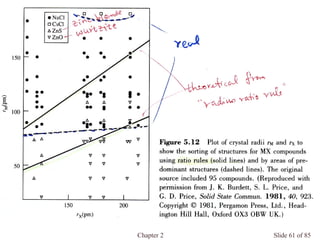
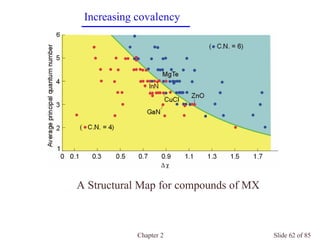
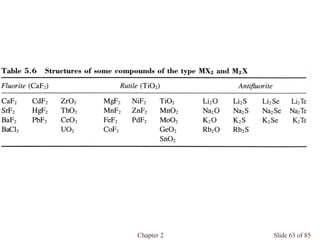
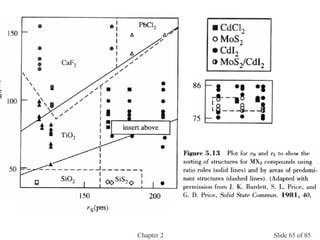
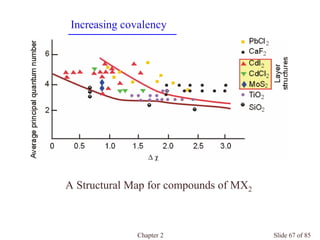
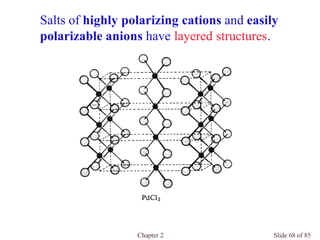
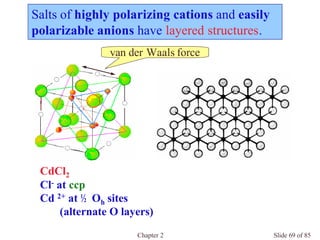
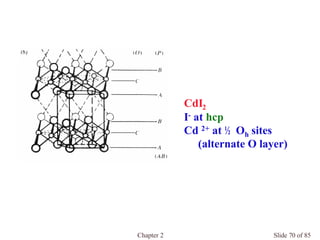
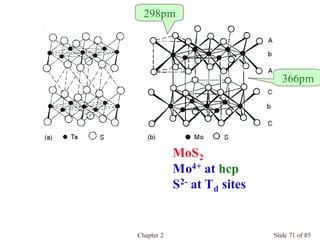
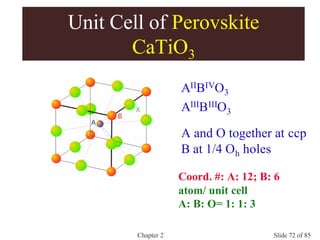
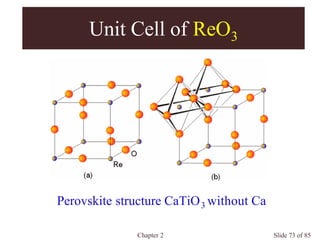
Chapter 2 discusses the structures of solids, focusing on crystalline solids and their characteristics, including the concept of polymorphism and allotropy in materials like carbon and iron. It elaborates on different crystal structures such as cubic lattices and their variations (simple cubic, body-centered cubic, and face-centered cubic), as well as techniques like x-ray diffraction for determining crystal structures. Additionally, the chapter addresses factors affecting lattice energy and covalent character in ionic compounds, illustrating through various examples such as sodium chloride and calcium fluoride.










![Chapter 2 Slide 16 of 85
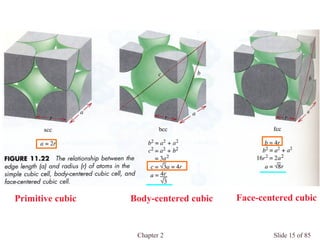
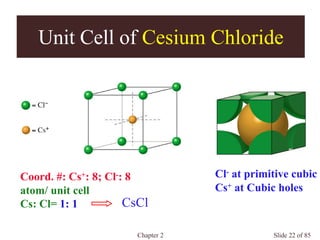
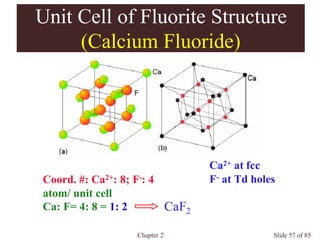
Occupancies per Unit Cells
Primitive cubic: a = 2r
1 atom/unit cell
occupancy = [4/3(πr3)]/a3 = [4/3(πr3)]/(2r)3
= 0.52 = 52%
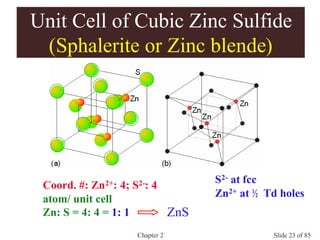
Body-centered cubic: a = 4r/(3)1/2
2 atom/unit cell
occupancy = 2 x [4/3(πr3)]/a3 = 2 x [4/3(πr3)]/[4r/(3)1/2]3
= 0.68 = 68%
Face-centered cubic: a = (8)1/2 r
4 atom/unit cell
occupancy = 4 x [4/3(πr3)]/a3 = 4 x [4/3(πr3)]/[(8)1/2 r]3
= 0.74 = 74%
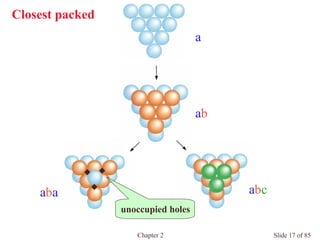
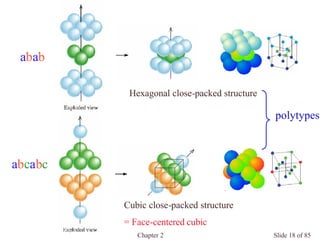
Closest packed](https://image.slidesharecdn.com/structuresofsolids-200516094044/85/Structures-of-solids-16-320.jpg)











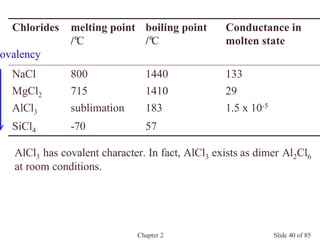
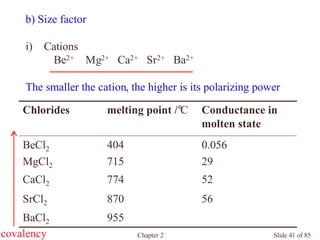

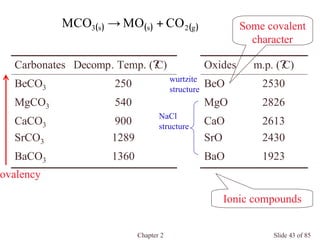
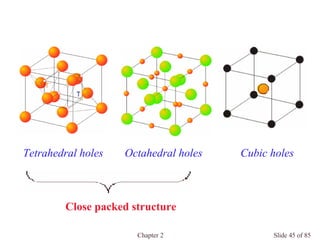
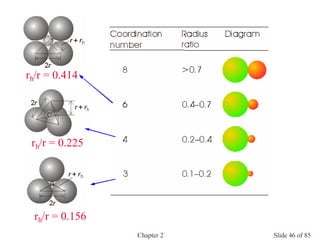
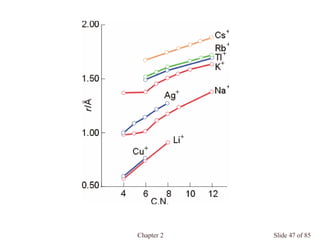
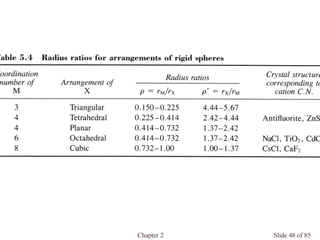


![Chapter 2 Slide 74 of 85
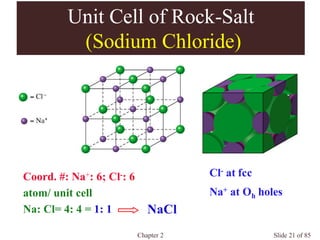
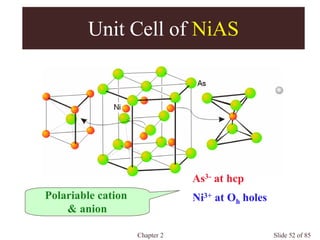
Unit Cell of Spinel
MgAl2O4
Normal Spinel
AII[BIII]2O4, AIV[BII]2O4 , AVI[BI]2O4
e.g. NiCr2O4, Co3O4 , Mn3O4
Inverse Spinel
B[AB]O4
e.g. Fe3O4
O 2- at fcc
A at 1/8 Td holes
B at 1/2 Oh holes](https://image.slidesharecdn.com/structuresofsolids-200516094044/85/Structures-of-solids-74-320.jpg)