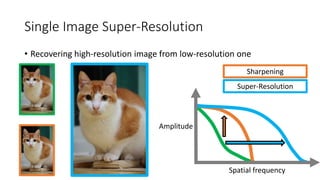
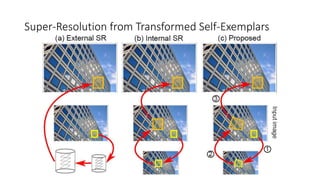
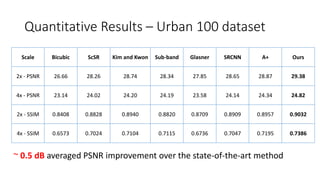
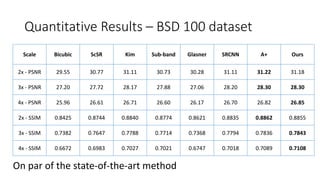
The document discusses a method for single image super-resolution using transformed self-exemplars, aiming to recover high-resolution images from low-resolution inputs without requiring external training data. It outlines various techniques and results, demonstrating improvements in performance on multiple datasets compared to state-of-the-art methods. The approach shows particular effectiveness for urban scenes, achieving comparable results while avoiding complex learning algorithms.

1. Single Image Super-Resolution from
Transformed Self-Exemplars
Jia-Bin Huang Narendra AhujaAbhishek Singh

2. Single Image Super-Resolution
• Recovering high-resolution image from low-resolution one
Spatial frequency
Amplitude
Super-Resolution
Sharpening

3. Multi-image vs. Single-image
Multi-image
Source: [Park et al. SPM 2003]
Single-image
Source: [Freeman et al. CG&A 2002]

4. External Example-based Super-Resolution
Learning to map from low-res to high-res patches
• Nearest neighbor [Freeman et al. CG&A 02]
• Neighborhood embedding [Chang et a. CVPR 04]
• Sparse representation [Yang et al. TIP 10]
• Kernel ridge regression [Kim and Kwon PAMI 10]
• Locally-linear regression [Yang and Yang ICCV 13] [Timofte et al. ACCV 14]
• Convolutional neural network [Dong et al. ECCV 14]
• Random forest [Schulter et al. CVPR 15]
External dictionary

5. Internal Example-based Super-Resolution
Low-res and high-res example pairs from patch
recurrence across scale
• Non-local means with self-examples [Ebrahimi and Vrscay ICIRA 2007]
• Unified classical and example SR [Glasner et al. ICCV 2009]
• Local self-similarity [Freedman and Fattal TOG 2011]
• In-place regression [Yang et al. ICCV 2013]
• Nonparametric blind SR [Michaeli and Irani ICCV 2013]
• SR for noisy images [Singh et al. CVPR 2014]
• Sub-band self-similarity [Singh et al. ACCV 2014]
Internal dictionary

6. Motivation
• Internal dictionary
• More “relevant” patches
• Limited number of examples
• High-res patches are often available in the transformed domain
Symmetry Surface orientation Perspective distortion

7. Super-Resolution from Transformed Self-Exemplars

8. LR input image Matching error LR patch HR patch
Translation
Perspective
Ground truth
LR/HR patch

9. Translation
Ground truth
LR/HR patch
Affine
transform
LR input image Matching error LR patch HR patch

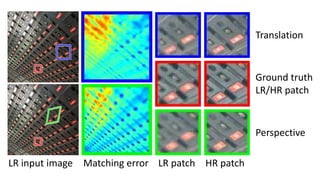
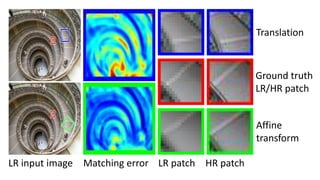
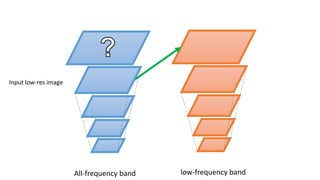
10. Input low-res image
All-frequency band low-frequency band
Super-Resolution Scheme
Multi-scale version of [Freedman and Fattal TOG 2011]

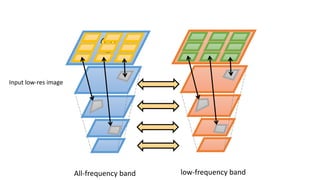
11. Input low-res image
LR/HR example pairs
Super-Resolution Scheme
Multi-scale version of [Freedman and Fattal TOG 2011]
low-frequency bandAll-frequency band

12. Input low-res image
low-frequency bandAll-frequency band

13. Input low-res image
low-frequency bandAll-frequency band

14. Super-Resolution as Nearest Neighbor Field Estimation
Appearance cost Plane compatibility Scale cost
[Huang et al. SIGGRAPH 2014] Scale

15. Search Patch Transformation
• Generalized PatchMatch [Barnes et al. ECCV 2010]
• Randomization
• Spatial propagation
• Backward compatible when planar structures were not detected
Perspective Similarity Affine
[Huang et al. SIGGRAPH 2014]

16. Results

17. Datasets – BSD 100 and Urban 100
Berkeley segmentation dataset (100 test images) Urban image dataset from Flickr (100 test images)

18. Dataset – Set5, Set14, and Sun-Hays 80
Set5
Set 14 Sun-Hays 80 [Sun and Hays ICCP 12]

19. Ground-truth HR
SRCNN [Dong et al. ECCV 14] Glasner [Glasner et al. ICCV 2009]
Our result
SR Factor 4x
Bicubic
A+ [Timofte et al. ACCV 14]

20. SR Factor 4x
Ground-truth HR
SRCNN [Dong et al. ECCV 14] Glasner [Glasner et al. ICCV 2009]
Our result
Bicubic
A+ [Timofte et al. ACCV 14]

21. SR Factor 4x
Ground-truth HR
SRCNN [Dong et al. ECCV 14] Glasner [Glasner et al. ICCV 2009]
Our result
Bicubic
A+ [Timofte et al. ACCV 14]

22. Bicubic
SRCNN [Dong et al. ECCV 14] A+ [Timofte et al. ACCV 14]
Our result
Ground-truth HR
Sub-band [Singh et al. ACCV 2014]

23. Ground-truth
SRCNN [Dong et al. ECCV 14]
Glasner [Glasner et al. ICCV 2009]
Our result

24. Ground-truth HR
SRCNN [Dong et al. ECCV 14]
Glasner [Glasner et al. ICCV 2009]
Our result

25. Bicubic
SRCNN [Dong et al. ECCV 14] A+ [Timofte et al. ACCV 14]
Our result
Ground-truth HR
Sub-band [Singh et al. ACCV 2014]

26. Bicubic
SRCNN [Dong et al. ECCV 14] A+ [Timofte et al. ACCV 14]
Our result
Ground-truth HR
Our resultSub-band [Singh et al. ACCV 2014]

27. Bicubic
SRCNN [Dong et al. ECCV 14] A+ [Timofte et al. ACCV 14]
Our result
Ground-truth HR
Glasner [Glasner et al. ICCV 2009]

28. Bicubic
SRCNN [Dong et al. ECCV 14] A+ [Timofte et al. ACCV 14]
Our result
Ground-truth HR
ScSR [Yang et al. TIP 10]

29. Bicubic
SRCNN [Dong et al. ECCV 14] A+ [Timofte et al. ACCV 14]
Our result
Ground-truth HR
ScSR [Yang et al. TIP 10]

30. Bicubic
SRCNN [Dong et al. ECCV 14] A+ [Timofte et al. ACCV 14]
Our result
Ground-truth HR
ScSR [Yang et al. TIP 10]

31. BSD 100 Dataset – SR factor 4x

32. Quantitative Results – Urban 100 dataset
Scale Bicubic ScSR Kim and Kwon Sub-band Glasner SRCNN A+ Ours
2x - PSNR 26.66 28.26 28.74 28.34 27.85 28.65 28.87 29.38
4x - PSNR 23.14 24.02 24.20 24.19 23.58 24.14 24.34 24.82
2x - SSIM 0.8408 0.8828 0.8940 0.8820 0.8709 0.8909 0.8957 0.9032
4x - SSIM 0.6573 0.7024 0.7104 0.7115 0.6736 0.7047 0.7195 0.7386
~ 0.5 dB averaged PSNR improvement over the state-of-the-art method

33. Quantitative Results – BSD 100 dataset
On par of the state-of-the-art method
Scale Bicubic ScSR Kim Sub-band Glasner SRCNN A+ Ours
2x - PSNR 29.55 30.77 31.11 30.73 30.28 31.11 31.22 31.18
3x - PSNR 27.20 27.72 28.17 27.88 27.06 28.20 28.30 28.30
4x - PSNR 25.96 26.61 26.71 26.60 26.17 26.70 26.82 26.85
2x - SSIM 0.8425 0.8744 0.8840 0.8774 0.8621 0.8835 0.8862 0.8855
3x - SSIM 0.7382 0.7647 0.7788 0.7714 0.7368 0.7794 0.7836 0.7843
4x - SSIM 0.6672 0.6983 0.7027 0.7021 0.6747 0.7018 0.7089 0.7108

34. Ground truth HR image
Input LR image
128 x 96

35. Bicubic SR Factor 8x

36. Internet-scale scene matching [Sun and Hays ICCP 12] SR Factor 8x
#Training images
6.3 millions

37. SRCNN [Dong et al. ECCV 14] SR Factor 8x
#Training images
395,909
from ImageNet

38. Our result SR Factor 8x
#Training image
1 LR input

39. Our result: coarse-to-fine super-resolution

40. Ground truth HR image
Input LR image
128 x 96

41. Bicubic SR Factor 8x

42. Sparse coding [Yang et al. TIP 10] SR Factor 8x

43. SRCNN [Dong et al. ECCV 14] SR Factor 8x

44. Our result SR Factor 8x

45. Our result: coarse-to-fine super-resolution

46. Ground truth HR image
Input LR image
128 x 96

47. Bicubic SR Factor 8x

48. SR Factor 8xInternet-scale scene matching [Sun and Hays ICCP 12]

49. SR Factor 8xSRCNN [Dong et al. ECCV 14]

50. Our result SR Factor 8x

51. Our result: coarse-to-fine super-resolution

52. Bicubic SR Factor 8x

53. SRCNN [Dong ECCV 2014] SR Factor 8x

54. Ours SR Factor 8x

55. Bicubic SR Factor 8x

56. SRCNN [Dong ECCV 2014] SR Factor 8x

57. Ours SR Factor 8x

58. Low-Res
TI-DTV
[Fernandez-Granda
and Candes ICCV 2013]
Ours
SR Factor 4x

59. Low-Res
TI-DTV
[Fernandez-Granda
and Candes ICCV 2013]
Ours
SR Factor 4x

60. Limitations – Blur Kernel Model
• Suffer from blur kernel mismatch
• Blind SR to estimate kernel
[Michaeli and Irani ICCV 2013]
[Efrat et al. ICCV 2013]
• With ground truth kernel, we can
get significantly improvement
• External example-based method
would need to retrain the model

61. Limitations
• Slow computation time
• On average, 40 seconds for super-resolving 2x on an image in BSD 100 dataset
on a 2.8Ghz PC, 12G RAM PC
SRF 4x
Ground truth HR Our result
A+ [Timofte et al. ACCV 14]SRCNN [Dong et al. ECCV 14]

62. Conclusions
• Super-resolution based on transformed self-exemplars
• No training data, no feature extraction, no complicated learning algorithms
• Works particularly well on urban scenes
• On par with state-of-the-art on natural scenes
Code and data available: http://bit.ly/selfexemplarsr
See us on poster #82

63. Single Image Super-Resolution
from Transformed Self-Exemplars
http://bit.ly/selfexemplarsr