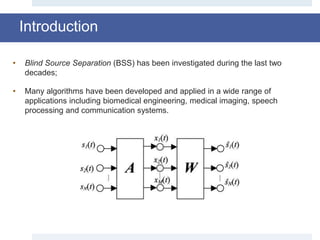
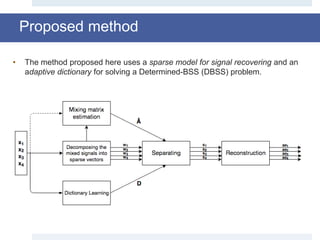
This document discusses a method for blind source separation (BSS) using dictionary learning, highlighting its relevance across various applications like biomedical engineering and communication systems. The proposed approach employs a sparse coding model with an adaptive dictionary to accurately estimate the mixing matrix and recover original sources from mixed signals. Experimental results indicate that the algorithm performs better with adaptive dictionaries compared to fixed ones, suggesting future work could explore undetermined BSS scenarios.

1. PARTHENOPE
UNIVERSITY
Blind Source Separation using
Dictionary Learning
Davide Nardone
October 24, 2016

2. Summary
1. Introduction
2. Blind Source Separation
3. Sparse Coding
4. Dictionary Learning
5. Proposed method
6. Experimental results
7. Real case study
8. Conclusions

3. • Blind Source Separation (BSS) has been investigated during the last two
decades;
• Many algorithms have been developed and applied in a wide range of
applications including biomedical engineering, medical imaging, speech
processing and communication systems.
Introduction

4. • Given m observations {x1,…,xm} where each {xi}i=1,…m is a row vector of size t,
each measurement is the linear mixture of n source processes:
• This linear mixture model is conveniently rewritten as:
X = AS + N
where A is the m×n mixing matrix, X is the m×t mixture of signals, S is the n×t
source data matrix and N is the m×t noise matrix.
BSS: Problem statement (1)
"i Î {1,…m}, xi = aijsj
j=1
n
å

5. • Usually in the BSS problem the only known information is the mixture X and the
number of sources.
• Ones need to determine both the mixing matrix A and the sources S, i.e.,
mathematically, one needs to solve
• It clear that such problem has an infinite number of solution, i.e., the problem is
ill-posed.
BSS: Problem statement (2)
min
A,S
X - AS F
2

6. BSS: Problem statement (3)
• The aim of BSS is to to estimate the S matrix from X, without the knowledge of
the the two matrices A and N.
• The BSS problem may be expressed in several ways, depending on the
number of sensors (m) and sources (n):
1. Under-determined case: m < n
2. Determined case: m = n
3. Over-determined case: m > n

7. • In order to find the true sources and the mixing matrix, it’s often required to add
extra constraints to the problem formulation.
• Most BSS techniques can be separated into two main classes, depending on
the way the sources are distinguished:
1. Statistical approach-ICA: well-known method called Independent Component
Analysis (ICA) assumes that the original sources {si}i=1,…,n are statistically
independent and non Gaussian. This has led to some widely approaches such as:
• Infomax
• Maximum likelihood estimation
• Maximum a posterior (MAP)
• FastICA
2. Sparsity/sparse approach: The basic assumption is that the sources are sparse in a
particular basis D and only a small number of sources differ significantly from zero.
BSS: Approaches

8. Sparse coding
• Given a signal x in Rm , we say it admits a sparse approximation α in Rk, when
one can find a linear combination of a few atoms from D that’s close to the
original signal.

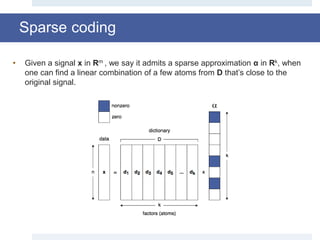
9. • Mathematically speaking we say that, since the signal x is a vector and the
dictionary D is a normalized basis, α in Rk is the vector that satisfies the
following optimization problem:
where ψ(α) is the l0 pseudo norm of α.
• In this form the optimization problem is NP-hard [1], but…
aÎÂk
min
1
2
x - Da 2
2
+ ly(a)
Sparse coding (cont.)

10. • Several techniques reduce this problem to a solvable problem that are
classified as:
1. Pursuit algorithms
2. Regularization algorithms
• Pursuit Algorithms are essentially greedy algorithms that try to find a sparse
representation one coefficient at time:
• It iteratively constructs a p-term approximation by maintaining a set of active columns
(initially set to zero) and expanding the set one column at time.
• After each iteration the residual is computed and the algorithm terminates whether it
becomes lower than a given threshold.
Sparse coding (cont.)

11. Orthogonal Matching Pursuit [2]
• Orthogonal Matching Pursuit(OMP) falls into the class of Pursuit Algorithms and
it’s able to identify the “best corresponding projections” of multidimensional data
over the span of a redundant dictionary D.
• Given a matrix of signals X = [x1,…,xn] in Rm×n and a dictionary D = [d1,…,dk] in
Rm×k, the algorithm computes a matrix A = [α1,…,αn] in Rk×n, where for each
column of X, it returns a coefficient vector α which is an approximation solution
of the following NP-hard problem [1]:
aÎÂk
min x - Da 2
2
s.t. a £ L
or
aÎÂk
min a 0
s.t. x - Da 2
2
£e
or
aÎÂk
min
1
2
x - Da 2
2
+ l a 0

12. The Dictionary Learning problem
• The “sparse signal decomposition” is mostly based on the degree of fitting
between the data and the dictionary, that leads to another important issue,
that is, the designing of the dictionary D.
• The most known approaches are:
1. Analytic approach
A mathematical model is given in advance so that a dictionary can be built by means of the
Discrete Cosine Transform (DCT), the Discrete Wavelet Transform (DWT), the Fast Four
Transform (FFT), etc.
2. Learning based approach
Machine Learning techniques are used for learning the dictionary from a set of data, so that its
atoms may represents the features of the signals.
• NB: The latter approach allows the model to be suitable for a broad class of
signals and it’s dependent on the underlying empirical data rather than a
theoretical model.

13. Learning based approach
• The method for learning the dictionary uses a training set of signals xi and it’s
equivalent to the following optimization problems:
• This problem tries to jointly find the sparse signal representation and the
dictionary so that all the representations are sparse.
Note, however, that the join optimization over both D and A is non-convex.
D,{ai }i=1
N
min ai 0
i=1
N
å s.t. xi - Dai 2
2
£e, 1£ i £ N
or
D,{ai }i=1
N
min xi - Dai 2
2
i=1
N
å s.t. ai 0
£ L, 1£ i £ N

14. Learning based approach (cont.)
• Packing all the x vectors into a matrix X in Rmxn and the corresponding sparse
representations into a matrix A in Rk×n, the dictionary D in Rm×k would satisfy
the following relation:
• In this work it’s been used the Method of Optimal Directions (MOD) and the
Online Dictionary Learning (ODL) for learning the dictionary.
• We have exclusively exanimated the resolution of BSS determined case using
an approach to Sparse Coding.
X = DA

15. Proposed method
• The method proposed here uses a sparse model for signal recovering and an
adaptive dictionary for solving a Determined-BSS (DBSS) problem.

16. Block signals representation
• The DBSS method proposed considers any kind of signals split into
blocks/patches.
• For instance, this process is used to correctly shape the training set matrix X
for the dictionary learning stage as well as for decomposing the generated
mixture.

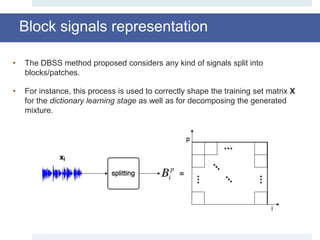
17. Dictionary Learning: MOD [3]
• This method views the problem posed in the previous equation as a nested
minimization problem:
1. An inner minimization to find a sparse representation A, given the source signals X
and dictionary D.
2. An outer minimization to find D.
• At the k-th step we have that:
D = D(k-1)
A = OMP(X,D)
• The techniques goes on for a defined number of iterations or until a
convergence criteria is satisfied.
D(k) =
D
argmin X - DA F
2
= XAk
T
(AAk
T
)-1
= XAk
+

18. Sparsifying the mixture
• Since the Separating Process exploits Compressive Sensing (CS) techniques,
it’s necessary to represent the mixture X = AS as a sparse matrix Xs.
• This process makes the Mixing Matrix Estimation and Recovering of Sources
processes computationally less expensive.
• To do so, we solve as many OMP problems as the number of the
blocks previously generated, followed by a step of reshaping and
concatenation.
• NB: The sparsity factor L (OMP parameter) used for obtaining the sparse
representation Xs might considerably impact on the estimation of the mixing matrix.
Bi
P

19. Mixing matrix estimation
• BSS approach may be divided into two categories:
• Methods which jointly estimate the mixing matrix and the signals and
• methods which first estimate the mixing matrix and then use it to reconstruct the
original signal.
• The method presented here is a two step methods since the separation and
reconstruction processes do not happen within the mixing estimation step.
• Due the lack of an efficient technique for estimating the mixing matrix from a
sparse mixture, here, for this project we’ve used the Generalized
Morphological Component Analysis (GMCA) [4] for estimating the mixing
matrix.

20. Mixing matrix estimation: GMCA
• GMCA is a novel approach that exploits both the morphological diversity and
sparsity of the signals.
• It’s a thresholding iterative algorithm where each sources and the
corresponding columns of A are estimated in an alternating way.
• The whole optimization schema progressively redefine the estimated sources S and
the mixing matrix A.
• Assuming that the dictionary D is redundant, this method is able to solve the
following optimization problem:
{ ˆA, ˆS}= arg min
A, S
k X - AS 2
2
+ S 0

21. Mixing matrix estimation: GMCA (2)
• GMCA algorithm is mainly made of two steps:
1. Estimate of S assuming A is fixed;
2. Compute of the mixing matrix A assuming S is fixed.
• The first step boils down to an estimate of the Least-Squares (LS) of the
sources, followed by a step of thresholding
• is the pseudo-inverse of the current estimated mixing matrix ;
• is a thresholding operator where is a threshold that decreases at each step.
• The second step is an update to the LS of the mixing matrix :
S = ld ( ˆA+
X)
ˆA+ ˆA
ld d
ˆA
ˆA = XST
(SST
)-1

22. Sparse source separation
• Once the mixing matrix is estimated, we formulate the DBSS problem as a
“recovery of sparse signal” by resolving T OMP problems for the following
expression:
where s(t) denotes the i-th sparse column vector of S at time t.
• The sources separation problem tries to find the vector s(t) given the
vector x(t) for all t.
• The problem of estimating the sparse representation of the signal sources is
equivalent to the following optimization problem:
ˆA
x(t) = As(t)+n(t), 1£ t £T
min
s(t)
s(t) 1
s.t. x(t)- As(t) 2
2
<e, t =1,…,T

23. Source reconstruction
ˆS = DS
• The sparse representations S, achieved at previous step, is then
expanded on the dictionary D for recovering the original sources.

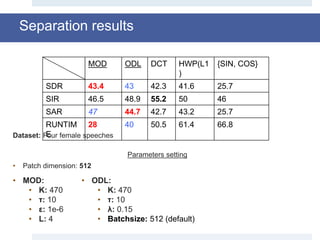
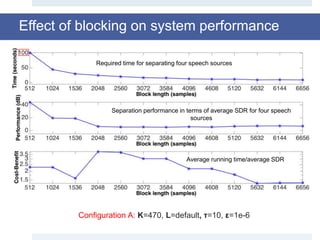
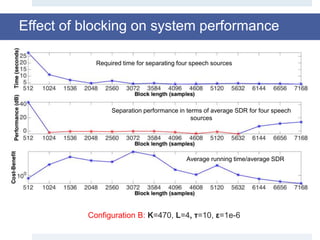
24. Experimental results
• Dataset: Sixth Community-Based Signal Separation Evaluation
Campaign, Sisec 2015 [5, 6].
• WAV audio file related to male or female voices and musical
instruments.
• Each source is sampled at16 KHz (160,000 sample), with a duration of 10 sec.
• All the results shown here have been averaged on 10 run, so that the
method could be statistically evaluated.
• The mixing matrix is randomly generated for each test, and the same
matrix is used in each run.

25. Evaluation metrics
• For objective quality assessment, we use three performance criteria defined in
the BSSEVAL toolbox [7] to evaluate the estimated source signals.
, e
• The estimated source can be composed as follows:
• According to [7], both SIR and SAR measure local performance,
• while SDR is global performance index, which may give better assessment to
the overall performance of the algorithms under comparison.
SDR =10log
starget
2
einterf +enoise +eartif
2
SIR =10log
starget
2
einterf
2
SAR =10log
starget +einterf +enoise
2
eartif
2

26. Separation performance: Fixed dictionary
• Fixed dictionary
• DCT
• Haar wavelet packet (level 1)
• {SIN, COS}
• It’s been used an ad hoc MATLAB function for building a dictionary D in
Rnxp.
• n: is the length of each column, depending on the length of the input
sources
• p: is the number of atoms.

27. Separation performance: Learned dictionary
• Strategies for learning the dictionary
• MOD
• ODL
• The parameters for learning the dictionary by using MOD are:
1. K: number atoms for the dictionary;
2. P: atom’s dimensionality ;
3. τ: number of iterations of the method;
4. ε: threshold on the squared l2-norm of the residual
5. L: maximum number of elements different from zero in each decomposition;
6. λ: penalty parameter.
• Because of the different approach used by ODL for learning the dictionary, the
parameters ε and L have been removed while λ has been set to 0.15.

28. Separation results
MOD ODL DCT HWP(L1
)
{SIN, COS}
SDR 43.4 43 42.3 41.6 25.7
SIR 46.5 48.9 55.2 50 46
SAR 47 44.7 42.7 43.2 25.7
RUNTIM
E
28 40 50.5 61.4 66.8
Dataset: Four female speeches
Parameters setting
• Patch dimension: 512
• MOD:
• K: 470
• τ: 10
• ε: 1e-6
• L: 4
• ODL:
• K: 470
• τ: 10
• λ: 0.15
• Batchsize: 512 (default)

29. Effect of blocking on system performance
Required time for separating four speech sources
Separation performance in terms of average SDR for four speech
sources
Average running time/average SDR
Configuration A: K=470, L=default, τ=10, ε=1e-6

30. Effect of blocking on system performance
Required time for separating four speech sources
Separation performance in terms of average SDR for four speech
sources
Average running time/average SDR
Configuration B: K=470, L=4, τ=10, ε=1e-6

31. Real case study: BSS in a Wireless Sensor Network
LEACH [8]
• A Wireless Sensor Network (WSN) is an interconnection of autonomous
sensors that:
1. Collect data from the environment.
2. Relay data through the network to
to a main location.
• Each node may be connect to
several other nodes, thus it may receive
a mixture of signals at its receiver.
• To transmit the message across the
network effectively, it’s necessary for
the receiver to separate the sources
from the mixture.

32. BSS for WSN(cont.)
• By using LEACH as protocol for a WSN, the following steps describe how the
proposed BSS method works in a real case study:
1. Learning stage: Data sample obtained from sensor node are used for building the
dictionary D (i.e. directly form the mixture)
2. Data transmission stage: Each sensor node sends at same time-instant t a
message containing information about the observed event.
3. Decomposing stage: The generic CH decomposes the signals mixture into a sparse
vectors which linked together generate the sparse signals mixture Xs.
4. Estimate mixing matrix stage: Basing on the the sparse mixture, each CH estimate
the de-mixing matrix by means of GMCA.
5. Sparse source separation stage: At each time instant t, the CH tries to find a vector
s(t) given x(t) and the de-mixing matrix.
6. Source reconstruction stage: Finally, the obtained sparse vectors are then
expanded using the dictionary D.

33. Conclusions
• The separation algorithm shows high accuracy results for a determined
BSS case.
• On average the algorithm seems to perform better with a adaptive
dictionary than with a fixed one.
Future works
• The method should be tested for an undetermined BSS case.
• The work can be extended to design dictionaries according to the
mixing matrix to ensure maximal separation.

34. [1] D. L. Donoho, “Compressed sensing,” IEEE Trans. Inform. Theory, vol. 52, no. 4, pp. 1289–1306, 2006.
[2] Y. C. Pati, R. Rezaiifar, and P. S. Krishnaprasad. "Orthogonal matching pursuit: Recursive function approximation with applications
to wavelet decomposition." IEEE Asilomar Conference on Signals, Systems and Computers, pp. 40-44., 1993.[2] Engan, Kjersti, Karl
Skretting, and John H°akon Husøy. ”Family of iterative LS-based dictionary learning algorithms, ILS-DLA, for sparse signal
representation.” Digital Signal Processing 17.1(2007): 32-49.
[3] Engan, Kjersti, Karl Skretting, and John H°akon Husøy. ”Family of iterative LS-based dictionary learning algorithms, ILS-DLA, for
sparse signal representation.” Digital Signal Processing 17.1 (2007): 32-49.
[4] Bobin, Jerome, et al. Sparsity and morphological diversity in blind source separation. IEEE Transactions on Image Processing 16.11
(2007): 2662-2674.
[5] E. Vincent, S. Araki, F.J. Theis, G. Nolte, P. Bofill, H. Sawada, A. Ozerov, B.V. Gowreesunker, D. Lutter and N.Q.K. Duong, The
Signal Separation Evaluation Campaign (2007-2010): Achievements and remaining challenges (external link), Signal Processing, 92,
pp. 1928-1936, 2012.
[6] E. Vincent, S. Araki and P. Bofill, The 2008 Signal Separation Evaluation Campaign: A community-based approach to large-scale
evaluation (external link), in Proc. Int. Conf. on Independen Component Analysis and Signal Separation, pp. 734-741, 2009.
[7] Vincent, E., Gribonval, R., Fevotte, C., 2006. Performance measurement in blind audio source separation. IEEE Trans. Audio,
Speech Language Process. 14 (4), 1462–1469.
[8] Heinzelman, W., Chandrakasan, A., and Balakrishnan, H., ”Energy-Efficient Communication Protocols for Wireless Microsensor
Networks”, Proceedings of the 33rd Hawaaian International Conference on Systems Science (HICSS), January 2000.
References

35. That’s all
−
Thank your for your attention.