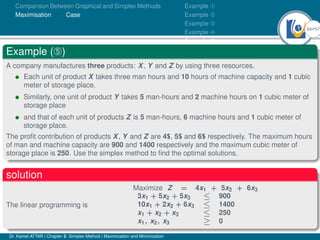
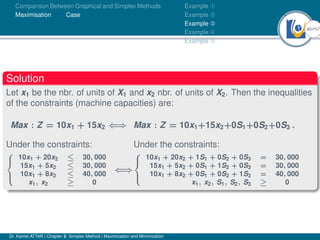
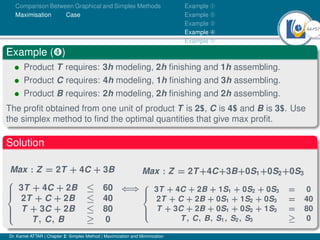
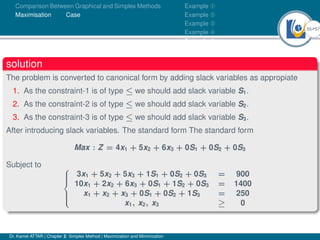
- The document discusses the comparison between graphical and simplex methods for solving linear programming problems involving maximization. - It explains that the graphical method is used for problems with two decision variables, while the simplex method can handle any number of decision variables. - The simplex method converts inequalities into equations by introducing slack or surplus variables, while the graphical method assumes inequalities are equations. 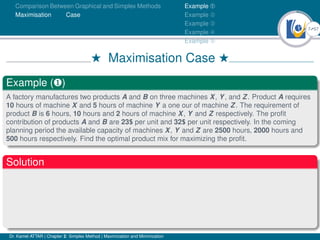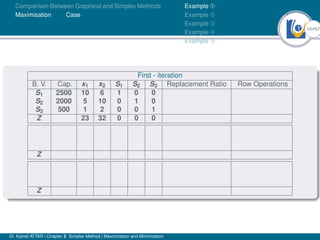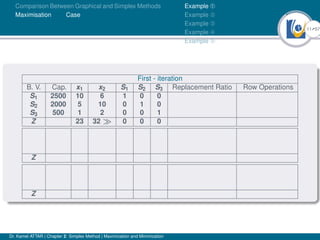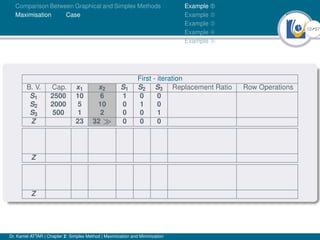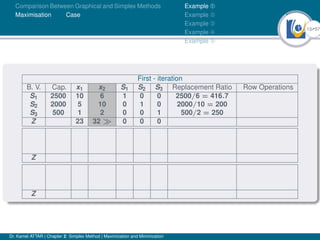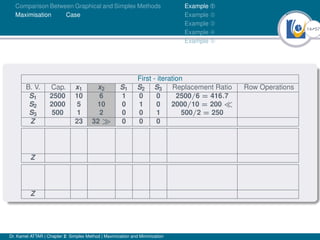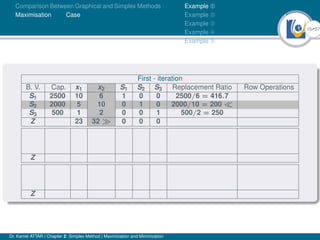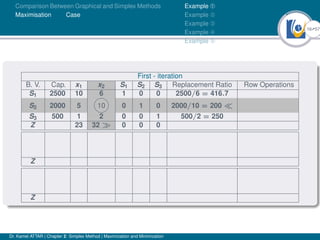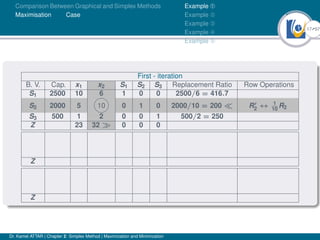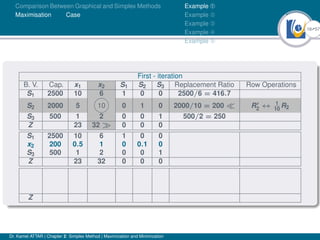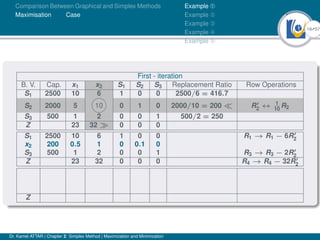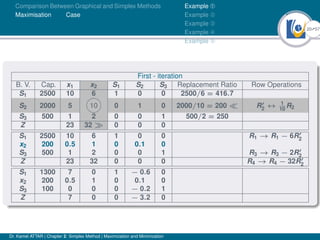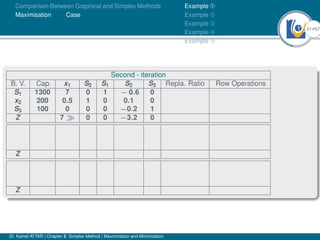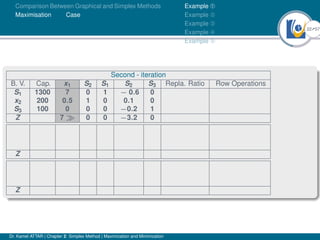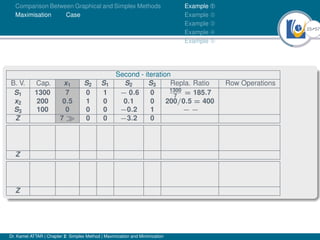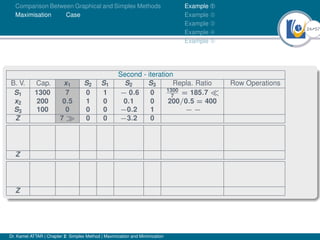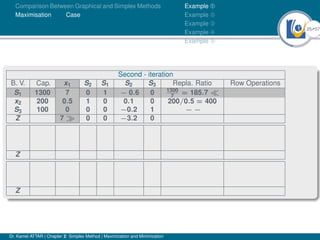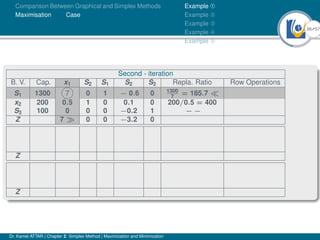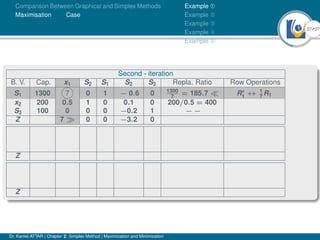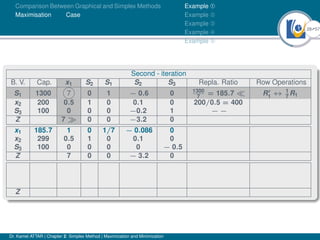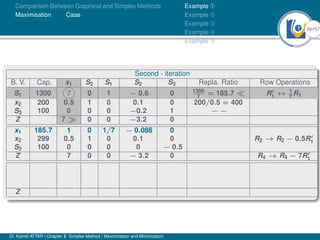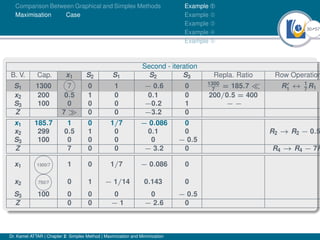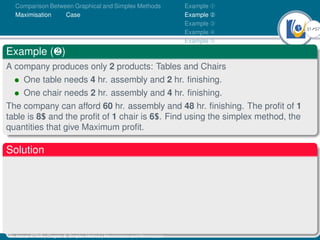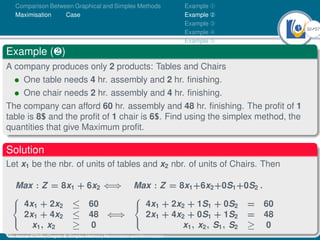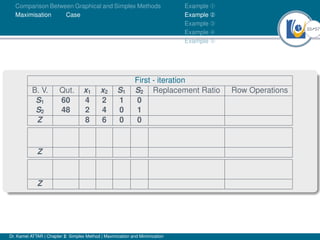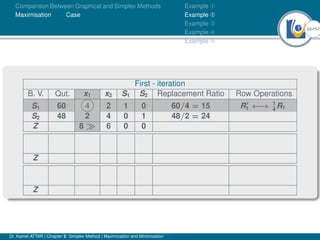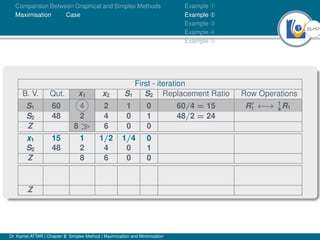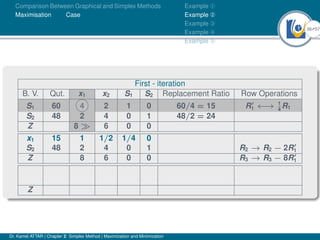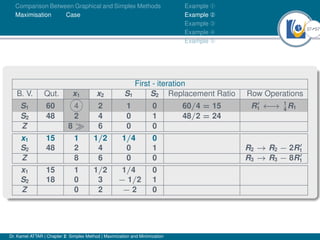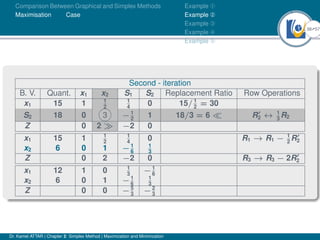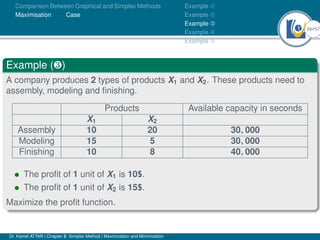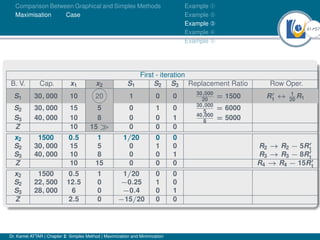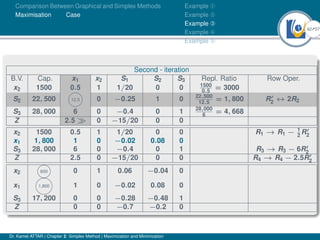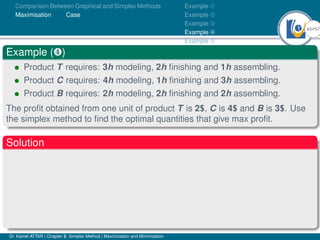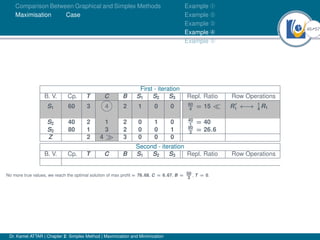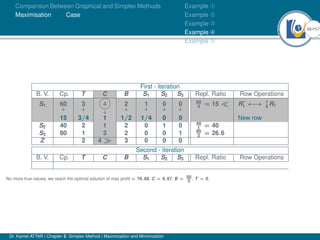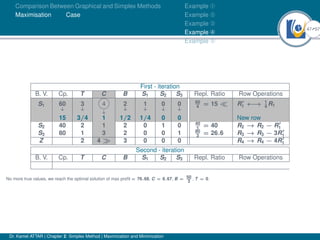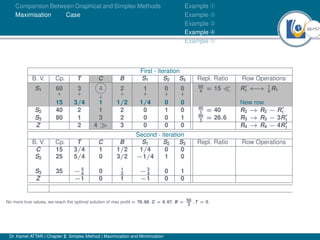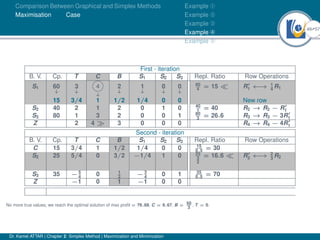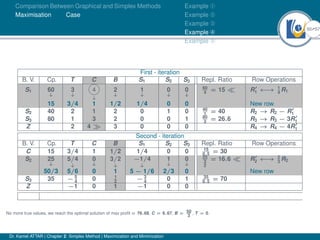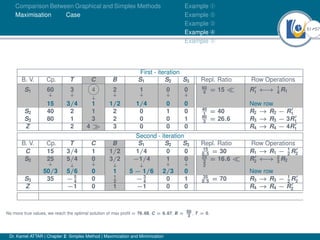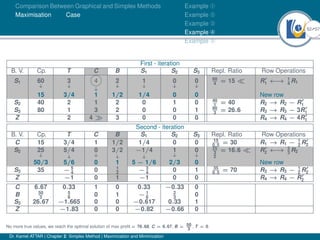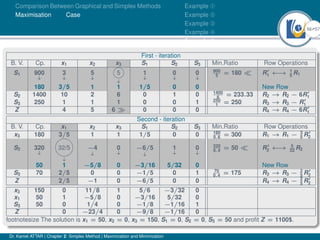- An example problem is presented and the first two iterations of the simplex method are shown to solve the problem and maximize profit.

1. Faculty of Economics and Business Administration
Lebanese University
Chapter 2: Simplex Method
(Maximization and Minimization)
Dr. Kamel ATTAR
attar.kamel@gmail.com
Lecture #3 F Monday 8/Mar/2021 F

2. 2Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
1 Comparison Between Graphical and Simplex Methods
2 Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

3. 3Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
H Comparison Between Graphical and Simplex Methods H
À I Graphical method is used when we have two decision variables in the
problem.
I Simplex method, is used when we have any number of decision variables.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

4. 4Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
H Comparison Between Graphical and Simplex Methods H
À I Graphical method is used when we have two decision variables in the
problem.
I Simplex method, is used when we have any number of decision variables.
Á I In graphical method, the inequalities are assumed to be equations, so as to
enable to draw straight lines.
I In Simplex method, the inequalities are converted into equations by:
(i) Adding a SLACK VARIABLE in maximisation problem.
(ii) Subtracting a SURPLUS VARIABLE in case of minimization problem.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

5. 5Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
H Comparison Between Graphical and Simplex Methods H
À I Graphical method is used when we have two decision variables in the
problem.
I Simplex method, is used when we have any number of decision variables.
Á I In graphical method, the inequalities are assumed to be equations, so as to
enable to draw straight lines.
I In Simplex method, the inequalities are converted into equations by:
(i) Adding a SLACK VARIABLE in maximisation problem.
(ii) Subtracting a SURPLUS VARIABLE in case of minimization problem.
 I In graphical method, the areas outside the feasible area (area covered by all
the lines of constraints in the problem) indicates idle capacity of resource
I In Simplex method, the presence of slack variable indicates the idle capacity
of the resources.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

6. 6Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
H Comparison Between Graphical and Simplex Methods H
À I Graphical method is used when we have two decision variables in the
problem.
I Simplex method, is used when we have any number of decision variables.
Á I In graphical method, the inequalities are assumed to be equations, so as to
enable to draw straight lines.
I In Simplex method, the inequalities are converted into equations by:
(i) Adding a SLACK VARIABLE in maximisation problem.
(ii) Subtracting a SURPLUS VARIABLE in case of minimization problem.
 I In graphical method, the areas outside the feasible area (area covered by all
the lines of constraints in the problem) indicates idle capacity of resource
I In Simplex method, the presence of slack variable indicates the idle capacity
of the resources.
à I In graphical method, if the isoprofit line coincides with more than one point of
the feasible polygon, then the problem has second alternate solution.
I In Simplex method, the netevaluation row has zero for non-basis variable the
problem has alternate solution.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

7. 7Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
H Maximisation Case H
Example (¶)
A factory manufactures two products A and B on three machines X, Y, and Z. Product A requires
10 hours of machine X and 5 hours of machine Y a one our of machine Z. The requirement of
product B is 6 hours, 10 hours and 2 hours of machine X, Y and Z respectively. The profit
contribution of products A and B are 23$ per unit and 32$ per unit respectively. In the coming
planning period the available capacity of machines X, Y and Z are 2500 hours, 2000 hours and
500 hours respectively. Find the optimal product mix for maximizing the profit.
Solution
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

8. 8Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
H Maximisation Case H
Example (¶)
A factory manufactures two products A and B on three machines X, Y, and Z. Product A requires
10 hours of machine X and 5 hours of machine Y a one our of machine Z. The requirement of
product B is 6 hours, 10 hours and 2 hours of machine X, Y and Z respectively. The profit
contribution of products A and B are 23$ per unit and 32$ per unit respectively. In the coming
planning period the available capacity of machines X, Y and Z are 2500 hours, 2000 hours and
500 hours respectively. Find the optimal product mix for maximizing the profit.
Solution
Machines Products Available capacity in hours
A B
X 10 6 2500
Y 5 10 2000
Z 1 2 500
Profit per unit in $ 23 32
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

9. 9Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Let the company manufactures x1 units of A and x2 units of B. Then the
inequalities of the constraints (machine capacities) are:
Max : Z = 23x1 + 32x2 ⇐⇒
Under the constraints:



10x1 + 6x2 ≤ 2500
5x1 + 10x2 ≤ 2000
x1 + 2x2 ≤ 500
⇐⇒
x1, x2 ≥ 0
Max : Z = 23x1+32x2+0S1+0S2+0S3 .
Under the constraints:



10x1 + 6x2 + 1S1 = 2500
5x1 + 10x2 + 1S2 = 2000
x1 + 2x2 + 1S3 = 500
x1, x2, S1, S2, S3 ≥ 0
Here we represent the idle capacity by means of a SLACK VARIABLE
represented by S. Slack variable for the first inequality is S1, that of the second
one is S2 and that of the n-th inequality is Sn.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

10. 10Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0
S2 2000 5 10 0 1 0
S3 500 1 2 0 0 1
Z 23 32 0 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

11. 11Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0
S2 2000 5 10 0 1 0
S3 500 1 2 0 0 1
Z 23 32 0 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

12. 12Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0
S2 2000 5 10 0 1 0
S3 500 1 2 0 0 1
Z 23 32 0 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

13. 13Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0 2500/6 = 416.7
S2 2000 5 10 0 1 0 2000/10 = 200
S3 500 1 2 0 0 1 500/2 = 250
Z 23 32 0 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

14. 14Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0 2500/6 = 416.7
S2 2000 5 10 0 1 0 2000/10 = 200
S3 500 1 2 0 0 1 500/2 = 250
Z 23 32 0 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

15. 15Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0 2500/6 = 416.7
S2 2000 5 10 0 1 0 2000/10 = 200
S3 500 1 2 0 0 1 500/2 = 250
Z 23 32 0 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

16. 16Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0 2500/6 = 416.7
S2 2000 5 10 0 1 0 2000/10 = 200
S3 500 1 2 0 0 1 500/2 = 250
Z 23 32 0 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

17. 17Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0 2500/6 = 416.7
S2 2000 5 10 0 1 0 2000/10 = 200 R0
2 ↔ 1
10
R2
S3 500 1 2 0 0 1 500/2 = 250
Z 23 32 0 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

18. 18Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0 2500/6 = 416.7
S2 2000 5 10 0 1 0 2000/10 = 200 R0
2 ↔ 1
10
R2
S3 500 1 2 0 0 1 500/2 = 250
Z 23 32 0 0 0
S1 2500 10 6 1 0 0
x2 200 0.5 1 0 0.1 0
S3 500 1 2 0 0 1
Z 23 32 0 0 0
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

19. 19Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0 2500/6 = 416.7
S2 2000 5 10 0 1 0 2000/10 = 200 R0
2 ↔ 1
10
R2
S3 500 1 2 0 0 1 500/2 = 250
Z 23 32 0 0 0
S1 2500 10 6 1 0 0 R1 → R1 − 6R0
2
x2 200 0.5 1 0 0.1 0
S3 500 1 2 0 0 1 R3 → R3 − 2R0
2
Z 23 32 0 0 0 R4 → R4 − 32R0
2
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

20. 20Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Operations
S1 2500 10 6 1 0 0 2500/6 = 416.7
S2 2000 5 10 0 1 0 2000/10 = 200 R0
2 ↔ 1
10
R2
S3 500 1 2 0 0 1 500/2 = 250
Z 23 32 0 0 0
S1 2500 10 6 1 0 0 R1 → R1 − 6R0
2
x2 200 0.5 1 0 0.1 0
S3 500 1 2 0 0 1 R3 → R3 − 2R0
2
Z 23 32 0 0 0 R4 → R4 − 32R0
2
S1 1300 7 0 1 − 0.6 0
x2 200 0.5 1 0 0.1 0
S3 100 0 0 0 − 0.2 1
Z 7 0 0 − 3.2 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

21. 21Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operations
S1 1300 7 0 1 − 0.6 0
x2 200 0.5 1 0 0.1 0
S3 100 0 0 0 −0.2 1
Z 7 0 0 −3.2 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

22. 22Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operations
S1 1300 7 0 1 − 0.6 0
x2 200 0.5 1 0 0.1 0
S3 100 0 0 0 −0.2 1
Z 7 0 0 −3.2 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

23. 23Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operations
S1 1300 7 0 1 − 0.6 0 1300
7
= 185.7
x2 200 0.5 1 0 0.1 0 200/0.5 = 400
S3 100 0 0 0 −0.2 1 − −
Z 7 0 0 −3.2 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

24. 24Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operations
S1 1300 7 0 1 − 0.6 0 1300
7
= 185.7
x2 200 0.5 1 0 0.1 0 200/0.5 = 400
S3 100 0 0 0 −0.2 1 − −
Z 7 0 0 −3.2 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

25. 25Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operations
S1 1300 7 0 1 − 0.6 0 1300
7
= 185.7
x2 200 0.5 1 0 0.1 0 200/0.5 = 400
S3 100 0 0 0 −0.2 1 − −
Z 7 0 0 −3.2 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

26. 26Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operations
S1 1300 7 0 1 − 0.6 0 1300
7
= 185.7
x2 200 0.5 1 0 0.1 0 200/0.5 = 400
S3 100 0 0 0 −0.2 1 − −
Z 7 0 0 −3.2 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

27. 27Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operations
S1 1300 7 0 1 − 0.6 0 1300
7
= 185.7 R0
1 ↔ 1
7
R1
x2 200 0.5 1 0 0.1 0 200/0.5 = 400
S3 100 0 0 0 −0.2 1 − −
Z 7 0 0 −3.2 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

28. 28Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operations
S1 1300 7 0 1 − 0.6 0 1300
7
= 185.7 R0
1 ↔ 1
7
R1
x2 200 0.5 1 0 0.1 0 200/0.5 = 400
S3 100 0 0 0 −0.2 1 − −
Z 7 0 0 −3.2 0
x1 185.7 1 0 1/7 − 0.086 0
x2 299 0.5 1 0 0.1 0
S3 100 0 0 0 0 − 0.5
Z 7 0 0 − 3.2 0
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

29. 29Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operations
S1 1300 7 0 1 − 0.6 0 1300
7
= 185.7 R0
1 ↔ 1
7
R1
x2 200 0.5 1 0 0.1 0 200/0.5 = 400
S3 100 0 0 0 −0.2 1 − −
Z 7 0 0 −3.2 0
x1 185.7 1 0 1/7 − 0.086 0
x2 299 0.5 1 0 0.1 0 R2 → R2 − 0.5R0
1
S3 100 0 0 0 0 − 0.5
Z 7 0 0 − 3.2 0 R4 → R4 − 7R0
1
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

30. 30Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Cap. x1 S2 S1 S2 S3 Repla. Ratio Row Operation
S1 1300 7 0 1 − 0.6 0 1300
7
= 185.7 R0
1 ↔ 1
7
R1
x2 200 0.5 1 0 0.1 0 200/0.5 = 400
S3 100 0 0 0 −0.2 1 − −
Z 7 0 0 −3.2 0
x1 185.7 1 0 1/7 − 0.086 0
x2 299 0.5 1 0 0.1 0 R2 → R2 − 0.5
S3 100 0 0 0 0 − 0.5
Z 7 0 0 − 3.2 0 R4 → R4 − 7R
x1 1300/7 1 0 1/7 − 0.086 0
x2 750/7 0 1 − 1/14 0.143 0
S3 100 0 0 0 0 − 0.5
Z 0 0 − 1 − 2.6 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

31. 31Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Example (·)
A company produces only 2 products: Tables and Chairs
• One table needs 4 hr. assembly and 2 hr. finishing.
• One chair needs 2 hr. assembly and 4 hr. finishing.
The company can afford 60 hr. assembly and 48 hr. finishing. The profit of 1
table is 8$ and the profit of 1 chair is 6$. Find using the simplex method, the
quantities that give Maximum profit.
Solution
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

32. 32Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Example (·)
A company produces only 2 products: Tables and Chairs
• One table needs 4 hr. assembly and 2 hr. finishing.
• One chair needs 2 hr. assembly and 4 hr. finishing.
The company can afford 60 hr. assembly and 48 hr. finishing. The profit of 1
table is 8$ and the profit of 1 chair is 6$. Find using the simplex method, the
quantities that give Maximum profit.
Solution
Let x1 be the nbr. of units of tables and x2 nbr. of units of Chairs. Then
Max : Z = 8x1 + 6x2 ⇐⇒



4x1 + 2x2 ≤ 60
2x1 + 4x2 ≤ 48
x1, x2 ≥ 0
⇐⇒
Max : Z = 8x1+6x2+0S1+0S2 .



4x1 + 2x2 + 1S1 + 0S2 = 60
2x1 + 4x2 + 0S1 + 1S2 = 48
x1, x2, S1, S2 ≥ 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

33. 33Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Qut. x1 x2 S1 S2 Replacement Ratio Row Operations
S1 60 4 2 1 0
S2 48 2 4 0 1
Z 8 6 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

34. 34Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Qut. x1 x2 S1 S2 Replacement Ratio Row Operations
S1 60 4 2 1 0 60/4 = 15 R0
1 ←→ 1
4
R1
S2 48 2 4 0 1 48/2 = 24
Z 8 6 0 0
Z
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

35. 35Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Qut. x1 x2 S1 S2 Replacement Ratio Row Operations
S1 60 4 2 1 0 60/4 = 15 R0
1 ←→ 1
4
R1
S2 48 2 4 0 1 48/2 = 24
Z 8 6 0 0
x1 15 1 1/2 1/4 0
S2 48 2 4 0 1
Z 8 6 0 0
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

36. 36Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Qut. x1 x2 S1 S2 Replacement Ratio Row Operations
S1 60 4 2 1 0 60/4 = 15 R0
1 ←→ 1
4
R1
S2 48 2 4 0 1 48/2 = 24
Z 8 6 0 0
x1 15 1 1/2 1/4 0
S2 48 2 4 0 1 R2 → R2 − 2R0
1
Z 8 6 0 0 R3 → R3 − 8R0
1
Z
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

37. 37Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Qut. x1 x2 S1 S2 Replacement Ratio Row Operations
S1 60 4 2 1 0 60/4 = 15 R0
1 ←→ 1
4
R1
S2 48 2 4 0 1 48/2 = 24
Z 8 6 0 0
x1 15 1 1/2 1/4 0
S2 48 2 4 0 1 R2 → R2 − 2R0
1
Z 8 6 0 0 R3 → R3 − 8R0
1
x1 15 1 1/2 1/4 0
S2 18 0 3 − 1/2 1
Z 0 2 − 2 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

38. 38Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B. V. Quant. x1 x2 S1 S2 Replacement Ratio Row Operations
x1 15 1 1
2
1
4
0 15/1
2
= 30
S2 18 0 3 −1
2
1 18/3 = 6 R0
2 ↔ 1
3
R2
Z 0 2 −2 0
x1 15 1 1
2
1
4
0 R1 → R1 − 1
2
R0
2
x2 6 0 1 −1
6
1
3
Z 0 2 −2 0 R3 → R3 − 2R0
2
x1 12 1 0 1
3
−1
6
x2 6 0 1 −1
6
1
3
Z 0 0 −5
3
−2
3
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

39. 39Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Example (¸)
A company produces 2 types of products X1 and X2. These products need to
assembly, modeling and finishing.
Products Available capacity in seconds
X1 X2
Assembly 10 20 30, 000
Modeling 15 5 30, 000
Finishing 10 8 40, 000
• The profit of 1 unit of X1 is 10$.
• The profit of 1 unit of X2 is 15$.
Maximize the profit function.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

40. 40Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Solution
Let x1 be the nbr. of units of X1 and x2 nbr. of units of X2. Then the inequalities
of the constraints (machine capacities) are:
Max : Z = 10x1 + 15x2 ⇐⇒
Under the constraints:



10x1 + 20x2 ≤ 30, 000
15x1 + 5x2 ≤ 30, 000
10x1 + 8x2 ≤ 40, 000
x1, x2 ≥ 0
⇐⇒
Max : Z = 10x1+15x2+0S1+0S2+0S3 .
Under the constraints:



10x1 + 20x2 + 1S1 + 0S2 + 0S3 = 30, 000
15x1 + 5x2 + 0S1 + 1S2 + 0S3 = 30, 000
10x1 + 8x2 + 0S1 + 0S2 + 1S3 = 40, 000
x1, x2, S1, S2, S3 ≥ 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

41. 41Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cap. x1 x2 S1 S2 S3 Replacement Ratio Row Oper.
S1 30, 000 10 20 1 0 0 30,000
20
= 1500 R0
1 ↔ 1
20
R1
S2 30, 000 15 5 0 1 0 30,000
5
= 6000
S3 40, 000 10 8 0 0 1 40,000
8
= 5000
Z 10 15 0 0 0
x2 1500 0.5 1 1/20 0 0
S2 30, 000 15 5 0 1 0 R2 → R2 − 5R0
1
S3 40, 000 10 8 0 0 1 R3 → R3 − 8R0
1
Z 10 15 0 0 0 R4 → R4 − 15R0
1
x2 1500 0.5 1 1/20 0 0
S2 22, 500 12.5 0 −0.25 1 0
S3 28, 000 6 0 −0.4 0 1
Z 2.5 0 −15/20 0 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

42. 42Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Second - iteration
B.V. Cap. x1 x2 S1 S2 S3 Repl. Ratio Row Oper.
x2 1500 0.5 1 1/20 0 0 1500
0.5
= 3000
S2 22, 500 12.5 0 −0.25 1 0 22,500
12.5
= 1, 800 R0
2 ↔ 2R2
S3 28, 000 6 0 −0.4 0 1 28,000
6
= 4, 668
Z 2.5 0 −15/20 0 0
x2 1500 0.5 1 1/20 0 0 R1 → R1 − 1
2
R0
2
x1 1, 800 1 0 −0.02 0.08 0
S3 28, 000 6 0 −0.4 0 1 R3 → R3 − 6R0
2
Z 2.5 0 −15/20 0 0 R4 → R4 − 2.5R0
2
x2 600 0 1 0.06 −0.04 0
x1 1,800 1 0 −0.02 0.08 0
S3 17, 200 0 0 −0.28 −0.48 1
Z 0 0 −0.7 −0.2 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

43. 43Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Example (¹)
• Product T requires: 3h modeling, 2h finishing and 1h assembling.
• Product C requires: 4h modeling, 1h finishing and 3h assembling.
• Product B requires: 2h modeling, 2h finishing and 2h assembling.
The profit obtained from one unit of product T is 2$, C is 4$ and B is 3$. Use
the simplex method to find the optimal quantities that give max profit.
Solution
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

44. 44Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Example (¹)
• Product T requires: 3h modeling, 2h finishing and 1h assembling.
• Product C requires: 4h modeling, 1h finishing and 3h assembling.
• Product B requires: 2h modeling, 2h finishing and 2h assembling.
The profit obtained from one unit of product T is 2$, C is 4$ and B is 3$. Use
the simplex method to find the optimal quantities that give max profit.
Solution
Max : Z = 2T + 4C + 3B







3T + 4C + 2B ≤ 60
2T + C + 2B ≤ 40
T + 3C + 2B ≤ 80
T, C, B ≥ 0
⇐⇒
Max : Z = 2T+4C+3B+0S1+0S2+0S3





3T + 4C + 2B + 1S1 + 0S2 + 0S3 = 0
2T + C + 2B + 0S1 + 1S2 + 0S3 = 40
T + 3C + 2B + 0S1 + 0S2 + 1S3 = 80
T, C, B, S1, S2, S3 ≥ 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

45. 45Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
S1 60 3 4 2 1 0 0 60
4 = 15 R0
1 ←
→ 1
4 R1
S2 40 2 1 2 0 1 0 40
1 = 40
S3 80 1 3 2 0 0 1 80
3 = 26.6
Z 2 4 3 0 0 0
Second - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
No more true values, we reach the optimal solution of max profit = 76.68, C = 6.67, B = 50
3
, T = 0.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

46. 46Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
S1 60
↓
3
↓
4
↓
2
↓
1
↓
0
↓
0
↓
60
4 = 15 R0
1 ←
→ 1
4 R1
15 3/4 1 1/2 1/4 0 0 New row
S2 40 2 1 2 0 1 0 40
1 = 40
S3 80 1 3 2 0 0 1 80
3 = 26.6
Z 2 4 3 0 0 0
Second - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
No more true values, we reach the optimal solution of max profit = 76.68, C = 6.67, B = 50
3
, T = 0.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

47. 47Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
S1 60
↓
3
↓
4
↓
2
↓
1
↓
0
↓
0
↓
60
4 = 15 R0
1 ←
→ 1
4 R1
15 3/4 1 1/2 1/4 0 0 New row
S2 40 2 1 2 0 1 0 40
1 = 40 R2 → R2 − R0
1
S3 80 1 3 2 0 0 1 80
3 = 26.6 R3 → R3 − 3R0
1
Z 2 4 3 0 0 0 R4 → R4 − 4R0
1
Second - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
No more true values, we reach the optimal solution of max profit = 76.68, C = 6.67, B = 50
3
, T = 0.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

48. 48Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
S1 60
↓
3
↓
4
↓
2
↓
1
↓
0
↓
0
↓
60
4 = 15 R0
1 ←
→ 1
4 R1
15 3/4 1 1/2 1/4 0 0 New row
S2 40 2 1 2 0 1 0 40
1 = 40 R2 → R2 − R0
1
S3 80 1 3 2 0 0 1 80
3 = 26.6 R3 → R3 − 3R0
1
Z 2 4 3 0 0 0 R4 → R4 − 4R0
1
Second - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
C 15 3/4 1 1/2 1/4 0 0
S2 25 5/4 0 3/2 −1/4 1 0
S3 35 − 5
4 0 1
2 − 3
4 0 1
Z −1 0 1 −1 0 0
No more true values, we reach the optimal solution of max profit = 76.68, C = 6.67, B = 50
3
, T = 0.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

49. 49Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
S1 60
↓
3
↓
4
↓
2
↓
1
↓
0
↓
0
↓
60
4 = 15 R0
1 ←
→ 1
4 R1
15 3/4 1 1/2 1/4 0 0 New row
S2 40 2 1 2 0 1 0 40
1 = 40 R2 → R2 − R0
1
S3 80 1 3 2 0 0 1 80
3 = 26.6 R3 → R3 − 3R0
1
Z 2 4 3 0 0 0 R4 → R4 − 4R0
1
Second - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
C 15 3/4 1 1/2 1/4 0 0 15
0.5 = 30
S2 25 5/4 0 3/2 −1/4 1 0 25
3
2
= 16.6 R0
2 ←
→ 2
3 R2
S3 35 − 5
4 0 1
2 − 3
4 0 1 35
0.5 = 70
Z −1 0 1 −1 0 0
No more true values, we reach the optimal solution of max profit = 76.68, C = 6.67, B = 50
3
, T = 0.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

50. 50Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
S1 60
↓
3
↓
4
↓
2
↓
1
↓
0
↓
0
↓
60
4 = 15 R0
1 ←
→ 1
4 R1
15 3/4 1 1/2 1/4 0 0 New row
S2 40 2 1 2 0 1 0 40
1 = 40 R2 → R2 − R0
1
S3 80 1 3 2 0 0 1 80
3 = 26.6 R3 → R3 − 3R0
1
Z 2 4 3 0 0 0 R4 → R4 − 4R0
1
Second - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
C 15 3/4 1 1/2 1/4 0 0 15
0.5 = 30
S2 25
↓
5/4
↓
0
↓
3/2
↓
−1/4
↓
1
↓
0
↓
25
3
2
= 16.6 R0
2 ←
→ 2
3 R2
50/3 5/6 0 1 5 − 1/6 2/3 0 New row
S3 35 − 5
4 0 1
2 − 3
4 0 1 35
0.5 = 70
Z −1 0 1 −1 0 0
No more true values, we reach the optimal solution of max profit = 76.68, C = 6.67, B = 50
3
, T = 0.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

51. 51Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
S1 60
↓
3
↓
4
↓
2
↓
1
↓
0
↓
0
↓
60
4 = 15 R0
1 ←
→ 1
4 R1
15 3/4 1 1/2 1/4 0 0 New row
S2 40 2 1 2 0 1 0 40
1 = 40 R2 → R2 − R0
1
S3 80 1 3 2 0 0 1 80
3 = 26.6 R3 → R3 − 3R0
1
Z 2 4 3 0 0 0 R4 → R4 − 4R0
1
Second - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
C 15 3/4 1 1/2 1/4 0 0 15
0.5 = 30 R1 → R1 − 1
2 R0
2
S2 25
↓
5/4
↓
0
↓
3/2
↓
−1/4
↓
1
↓
0
↓
25
3
2
= 16.6 R0
2 ←
→ 2
3 R2
50/3 5/6 0 1 5 − 1/6 2/3 0 New row
S3 35 − 5
4 0 1
2 − 3
4 0 1 35
0.5 = 70 R3 → R3 − 1
2 R0
2
Z −1 0 1 −1 0 0 R4 → R4 − R0
2
No more true values, we reach the optimal solution of max profit = 76.68, C = 6.67, B = 50
3
, T = 0.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

52. 52Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
S1 60
↓
3
↓
4
↓
2
↓
1
↓
0
↓
0
↓
60
4 = 15 R0
1 ←
→ 1
4 R1
15 3/4 1 1/2 1/4 0 0 New row
S2 40 2 1 2 0 1 0 40
1 = 40 R2 → R2 − R0
1
S3 80 1 3 2 0 0 1 80
3 = 26.6 R3 → R3 − 3R0
1
Z 2 4 3 0 0 0 R4 → R4 − 4R0
1
Second - iteration
B. V. Cp. T C B S1 S2 S3 Repl. Ratio Row Operations
C 15 3/4 1 1/2 1/4 0 0 15
0.5 = 30 R1 → R1 − 1
2 R0
2
S2 25
↓
5/4
↓
0
↓
3/2
↓
−1/4
↓
1
↓
0
↓
25
3
2
= 16.6 R0
2 ←
→ 2
3 R2
50/3 5/6 0 1 5 − 1/6 2/3 0 New row
S3 35 − 5
4 0 1
2 − 3
4 0 1 35
0.5 = 70 R3 → R3 − 1
2 R0
2
Z −1 0 1 −1 0 0 R4 → R4 − R0
2
C 6.67 0.33 1 0 0.33 −0.33 0
B 50
3
5
6 0 1 − 1
6
2
3 0
S3 26.67 −1.665 0 0 −0.617 0.33 1
Z −1.83 0 0 −0.82 −0.66 0
No more true values, we reach the optimal solution of max profit = 76.68, C = 6.67, B = 50
3
, T = 0.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

53. 53Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Example (Ä)
A company manufactures three products: X, Y and Z by using three resources.
• Each unit of product X takes three man hours and 10 hours of machine capacity and 1 cubic
meter of storage place.
• Similarly, one unit of product Y takes 5 man-hours and 2 machine hours on 1 cubic meter of
storage place
• and that of each unit of products Z is 5 man-hours, 6 machine hours and 1 cubic meter of
storage place.
The profit contribution of products X, Y and Z are 4$, 5$ and 6$ respectively. The maximum hours
of man and machine capacity are 900 and 1400 respectively and the maximum cubic meter of
storage place is 250. Use the simplex method to find the optimal solutions.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

54. 54Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
Example (Ä)
A company manufactures three products: X, Y and Z by using three resources.
• Each unit of product X takes three man hours and 10 hours of machine capacity and 1 cubic
meter of storage place.
• Similarly, one unit of product Y takes 5 man-hours and 2 machine hours on 1 cubic meter of
storage place
• and that of each unit of products Z is 5 man-hours, 6 machine hours and 1 cubic meter of
storage place.
The profit contribution of products X, Y and Z are 4$, 5$ and 6$ respectively. The maximum hours
of man and machine capacity are 900 and 1400 respectively and the maximum cubic meter of
storage place is 250. Use the simplex method to find the optimal solutions.
solution
The linear programming is
Maximize Z = 4x1 + 5x2 + 6x3
3x1 + 5x2 + 5x3 ≤ 900
10x1 + 2x2 + 6x3 ≤ 1400
x1 + x2 + x3 ≤ 250
x1, x2, x3 ≥ 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

55. 55Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
solution
The problem is converted to canonical form by adding slack variables as appropiate
1. As the constraint-1 is of type ≤ we should add slack variable S1.
2. As the constraint-2 is of type ≤ we should add slack variable S2.
3. As the constraint-3 is of type ≤ we should add slack variable S3.
After introducing slack variables. The standard form The standard form
Max : Z = 4x1 + 5x2 + 6x3 + 0S1 + 0S2 + 0S3
Subject to 






3x1 + 5x2 + 5x3 + 1S1 + 0S2 + 0S3 = 900
10x1 + 2x2 + 6x3 + 0S1 + 1S2 + 0S3 = 1400
x1 + x2 + x3 + 0S1 + 0S2 + 1S3 = 250
x1, x2, x3 ≥ 0
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

56. 56Ú57
Comparison Between Graphical and Simplex Methods
Maximisation Case
Example À
Example Á
Example Â
Example Ã
Example Ä
First - iteration
B. V. Cp. x1 x2 x3 S1 S2 S3 Min.Ratio Row Operations
S1 900
↓
3
↓
5
↓
5
↓
1
↓
0
↓
0
↓
900
5 = 180 R0
1 ←
→ 1
5 R1
180 3/5 1 1 1/5 0 0 New Row
S2 1400 10 2 6 0 1 0 1400
6 = 233.33 R2 → R2 − 6R0
1
S3 250 1 1 1 0 0 1 250
1 = 250 R3 → R3 − R0
1
Z 4 5 6 0 0 0 R4 → R4 − 6R0
1
Second - iteration
B. V. Cp. x1 x2 x3 S1 S2 S3 Min.Ratio Row Operations
x3 180 3/5 1 1 1/5 0 0 180
0.6 = 300 R1 → R1 − 3
5 R0
2
S2 320
↓
32/5
↓
−4
↓
0
↓
−6/5
↓
1
↓
0
↓
320
6.4 = 50 R0
2 ←
→ 5
32 R2
50 1 −5/8 0 −3/16 5/32 0 New Row
S3 70 2/5 0 0 −1/5 0 1 70
0.4 = 175 R3 → R3 − 2
5 R0
2
Z 2/5 −1 0 −6/5 0 0 R4 → R4 − 2
5 R0
2
x3 150 0 11/8 1 5/6 −3/32 0
x1 50 1 −5/8 0 −3/16 5/32 0
S3 50 0 1/4 0 −1/8 −1/16 1
Z 0 −23/4 0 −9/8 −1/16 0
footnotesize The solution is x1 = 50, x2 = 0, x3 = 150, S1 = 0, S2 = 0, S3 = 50 and profit Z = 1100$.
Dr. Kamel ATTAR | Chapter 2: Simplex Method | Maximization and Minimization

57. Thank you! Questions?